Можно ли сдать базу математику в 10 классе егэ: Сдать ЕГЭ в 10 классе

Сдать ЕГЭ в 10 классе

ЕГЭ – это форма государственной итоговой аттестации выпускников школ и одновременно вступительные экзамены в вузы. Однако ЕГЭ по некоторым предметам все школьники, при желании, могут сдать уже в 10 классе. Это география, русский язык и математика (базовый уровень) – дисциплины, программа изучения которых завершается как раз к концу 10 класса. Чтобы сдать ЕГЭ заранее, десятикласснику нужно до 1 февраля текущего учебного года написать соответствующее заявление в своей школе и постараться не выйти троечником по этим предметам за год. И в мае-июне можно будет сдавать ЕГЭ наравне с выпускниками 11 классов.

Если полученные результаты устроят школьника, то через год он сможет их использовать при поступлении в вуз. Если нет, то ЕГЭ можно будет беспрепятственно пересдать уже после 11 класса, а при подаче заявления в вуз, указать любой из двух полученных результатов (какой больше нравится).

Кроме того, если сдать ЕГЭ по русскому языку и базовой математике в 10 классе, то на следующий год уроки по этим предметам в школе можно будет вполне обоснованно не посещать и не делать лишних домашних заданий.

Разве что вы не планируете сдавать профильный ЕГЭ по математике после 11 класса.

Сдать ЕГЭ в 10 классе по остальным предметам тоже возможно. Для этого опять же необходимо успешно (на итоговую оценку «хорошо» или «отлично») завершить программу изучения выбранной дисциплины. Но что делать, если изучение всех предметов кроме географии, русского языка и математики базового уровня продолжается в 11 классе? Придётся осваивать программу самостоятельно и экстерном. В первую очередь такой вариант возможен для школьников, которые находится на семейном или дистанционном обучении и учиться по индивидуальной программе. Однако перейти на семейное или дистанционное обучение может любой и когда угодно.

Подробнее о том, как перейти на семейное обучение>>

Какой бы предмет вы не выбрали к сдаче на ЕГЭ в 10 классе, итоговое сочинение всё равно придётся писать только после окончания 11 класса. Парадоксально, но, даже не смотря на то, что «зачет» по итоговому сочинению (изложению) является допуском к итоговой аттестации после 11 класса, написать его заранее нельзя. Исключение делается только для тех, кто освоил программу среднего общего образования экстерном.

Рособрнадзор предложил вернуть ЕГЭ по базовой математике — РБК

В этом году выпускники школ, которые планировали поступить в вуз, не сдавали обязательный ЕГЭ по базовой математике. Для получения аттестата им было достаточно сдать экзамен по русскому

Фото: Кирилл Кухмарь / ТАСС

Рособрнадзор предлагает вернуть в России в 2022 году Единый государственный экзамен (ЕГЭ) по базовой математике для выпускников школ.

Об этом сообщил руководитель Федеральной службы по надзору в сфере образования и науки Анзор Музаев на всероссийской встрече с родителями школьников, передает ТАСС.

«У нас и у Министерства просвещения позиция такая, чтобы вернуть базовую математику, как обязательный предмет для тех, кто получает аттестат и не выбрал его [предмет] для поступления в вуз», — сказал он.

Рособрнадзор назвал необоснованной идею о полном отказе от ЕГЭ

В этом году обязательный ЕГЭ по базовой математике отменили для учеников 11-х классов из-за коронавируса. Для получения аттестата было достаточно сдать ЕГЭ по русскому языку. При этом те, кто не планировал поступать в вузы после 11-го класса, вместо ЕГЭ могли пройти государственный выпускной экзамен (ГВЭ) по русскому языку и математике.

Знали ли вы, что ЕГЭ можно сдать в 10 классе? | Подслушано ЕГЭ

Моя история в чем-то уникальна. Дело в том, что мы с одноклассницей сдали ЕГЭ по русскому в 10 классе. (Да, представляете, так было можно!) Узнала я о такой возможности совершенно случайно в середине года. К сожалению, в школах об этом почему-то не говорят. Поэтому я очень хочу поделиться своим опытом.

Итак, во-первых, в конце 10 класса ученики могут по желанию сдать ЕГЭ по русскому, базовой математике или географии. Если результаты их не устроят, они могут ПЕРЕСДАТЬ эти предметы в 11 классе вместе с учениками прошлых лет и взрослыми, которые сдают ЕГЭ по желанию. Во-вторых, чтобы получить разрешение на сдачу того или иного предмета, нужно самостоятельно пройти программу 10-го и 11-ого классов и сдать учителю зачеты для получения оценок за четверти. В-третьих, это достаточно серьезная морока (особенно для учителей, как я понимаю), поэтому такая досрочная сдача не распространена. В нашем регионе (Алтайский край) это вообще была ПЕРВАЯ подобная попытка за все года.

Если бы в школах говорили о возможности сдачи экзамена в 10 классе, это бы упростило ситуацию. Но я узнала об этом в конце января. Причем все учителя пытались отговорить нас с подругой, пришлось подключать родителей, копаться в законах и разбираться что к чему. Кстати, в законах этот момент прописан не очень понятно, но никто не имеет права запрещать десятикласснику сдавать ЕГЭ в 10-ом классе. Однако для этого нужно переходить на индивидуальный план обучения, чтобы освоить программу двух годов досрочно.

Надо сказать, было страшно. Такая авантюра стала серьезным испытанием. Я всегда хорошо знала русский: врожденная грамотность, сочинения на пятерки… Но пришлось сильно пахать, чтобы достичь результата.

Кстати о нем. У меня 96 баллов. У моей подруги – 89. Честно говоря, до сих пор не верю, что все это было не напрасно. Пробники я писала максимум на 86, а на самом ЕГЭ еще и текст попался сложный.

Кратко о подготовке

В толстую тетрадь я выписывала теорию, правила. Для меня это было в новинку, так как я никогда не уделяла особого внимания теории по русскому. Но без этого хорошо сдать ЕГЭ невозможно, даже если есть «чувство языка», интуиция и все остальное. Прорешала (без сочинения) все варианты тестовых заданий в сборнике Цыбулько и еще где-то 30 вариантов из сборника Васильевых и Гостевой. Плюс несколько вариантов на сайте «РЕШУ ЕГЭ» (кстати, там они сложнее) Самой большой проблемой стали сочинения, потому что, естественно, в школе мы их практически не разбирали. Хорошо, что наша учительница по русскому смогла неплохо объяснить, что от нас требуется и какого плана придерживаться. Еще одна проблема – пробники. Если в 11-ом классе их пишут все и пишут часто, то мы… Два раза мы ходили на платные пробники в университет, еще один – в центр тестирования. Все самостоятельно, за свой счет. В школе, конечно, для нас никаких пробников в 10-ом классе не было. Еще один провела наша учительница русского в качестве последнего зачета (оценка за 2-ое полугодие 11-ого класса).

Сам экзамен прошел довольно мирно. Разве что мы с подругой были там единственными десятиклассниками. На бланке так и писали – 10 класс. Особенных неожиданностей не было. Правда, времени едва хватило. Я закончила минуты за 2 до конца, едва успела пробежаться глазами по сочинению, чтобы проверить. Текст попался довольно сложный. Я уже смирилась с плохим результатом и разочаровалась в этой затее, когда увидела в интернете результаты. 96 баллов – не идеальный результат, но в данной ситуации я и о таком не мечтала.

Итак, подведу итоги. ЕГЭ можно сдавать в 10-ом классе. В случае неудовлетворительных результатов – пересдать в 11 классе (Собственно, каждый имеет право сдавать ЕГЭ хоть каждый год). Я бы очень хотела, чтобы как можно больше учеников знали о такой возможности. Не все ей воспользуются, не всем это надо, и, возможно, не всем стоит пробовать. Но знать люди имеют право. Так что поделитесь этой информацией с теми, кто переходит сейчас в 10-ый или 9-ый класс.

Мне же предстоит сдавать еще ЕГЭ через год. Надеюсь, результаты будут не хуже. Поздравляю тех, кто сдал экзамены, и желаю удачи тем, кто только собирается их сдавать.

P.s./опыт нашей читательницы

Как изменится ЕГЭ и ОГЭ в 2022 году: 10 важных ответов

В Рособрнадзоре уверены: новые задания дают больше возможности проявить себя Фото: Анна Майорова © URA.RU

Единый госэкзамен в 2022 году существенно изменится. Родителям выпускников объяснили, сколько предметов и в каком формате нужно будет сдавать на ЕГЭ и ОГЭ, зачем усложнили математику и обществознание, когда обновится открытый банк заданий ФИПИ и будут ли школьники писать экзамен дистанционно. Об этом — руководитель Рособрнадзора Анзор Музаев и директор Федерального института педагогических измерений Оксана Решетникова.

Сколько экзаменов нужно сдавать?

Статья по теме

Как рассказал руководитель Рособрнадзора Анзор Музаев в рамках Всероссийской онлайн-встречи с родителями, сейчас они отправили на рассмотрение в Минпросвещения РФ предложение вернуться к доковидным порядкам проведения экзаменов. «Объявлять о том, что не будет экзаменов, я не хочу», — подчеркнул чиновник.

В частности, речь идет о том, чтобы в 9 классе было два обязательных предмета для сдачи ОГЭ — русский язык и математика — и два по выбору. Точно так же должно быть в ЕГЭ в 11 классе. В том числе Рособрнадзор намерен вернуть в качестве обязательного предмета базовую математику: для тех, кто хочет получить аттестат и не выбирает профильную математику, которая требуется по ряду специальностей.

Зачем усложнили математику?

В онлайн-встрече с родителями также участвовала директор Федерального института педагогических измерений (ФИПИ, учредитель — Рособрнадзор) Оксана Решетникова. Она помогала с ответами про изменения КИМ (контрольных измерительных материалов) ЕГЭ в 2022 году.

К примеру, она объяснила, зачем усложнили экзамен по профильной математике: «Профильная математика избавилась от балласта (заданий, которые выполнялись всеми ребятами), который мало дифференцировал [детей] по уровню подготовленности, мало говорил о том потенциале ребенка, который пригодится в технических, инженерных вузах». При этом, по словам Решетниковой, внеслись задания, дающие ребятам больше возможности проявить себя.

Итоговые сочинения проверяют вручную

Родители спросили главу Рособрнадзора о том, как оценивается одно из требований итогового сочинения — самостоятельность написания (наличие заимствований — прим. URA.RU). «Проверка — это ручная работа. Программного обеспечения для этого у нас нет. Проверяет эксперт, учитель», — лаконично ответил Музаев.

Новых обязательных предметов для ЕГЭ не будет еще долго

Фото: Владимир Жабриков © URA. RU

Все одиннадцатиклассники перед экзаменами пишут итоговое сочинение. В этом учебном году оно запланировано на 1 декабря (дополнительные дни — 2 февраля и 4 мая 2022 года). Ранее ученые и репетиторы рассказали URA.RU, как лучше всего готовиться к сочинению и ЕГЭ по русскому языку.

Зачем ускорили ЕГЭ по обществознанию?

В проекте изменений КИМ единого госэкзамена по обществознанию и истории в 2022 году было обозначено уменьшение времени, данного для ЕГЭ, — с 235 до 180 минут. Как заметила Решетникова, в экзаменах по этим предметам были убраны задания, которые в последние годы сводились к натаскиванию. «Создаются шаблоны, и мы видим несамостоятельные сочинения, которые уже не несут в себе никакого содержательного значения. Мы их изъяли, но именно они были самыми объемными по времени». Кроме того, уточнила она, другие объемные задания были заменены другими, где ответ в разы короче.

В октябре в рамках онлайн-консультаций Рособрнадзора руководитель комиссии по разработке КИМ ЕГЭ по обществознанию Татьяна Лискова заявила, что составители экзамена решают, сколько времени все-таки добавить.

Появятся ли новые дополнительные предметы?

Рособрнадзор постоянно спрашивают, когда и какие предметы станут обязательными наравне с русским языком и математикой. По словам Музаева, каждый пытается выйти с такой инициативой — продвинуть предмет, который любит. «Все предметы важны. Позиция Минпросвещения и наша: та модель, которая существует, — самодостаточна. И мы не планируем вводить дополнительно какой-то обязательный предмет», — успокоил чиновник.

Когда обновится открытый банк заданий ФИПИ?

Окончательных демонстрационных вариантов еще нет

Фото: Вадим Ахметов © URA.RU

Как пояснила директор ФИПИ, с августа идет общественное обсуждение предложенных изменений в ЕГЭ 2022 года. Разработка банка заданий началась одновременно с этим. «В январе мы опубликуем новые задания в банке и обновим навигатор подготовки к ЕГЭ», — заверила Решетникова.

Она дополнила, что в каждом КИМе свою форму изменили не более 3-4 заданий. Содержание осталось прежним. До обновления банка Решетникова предложила ознакомиться с форматом заданий в демонстрационном варианте экзамена (выложен на сайте ФИПИ) и начать подготовку к ЕГЭ. По ее словам, сейчас заканчивается общественно-профессиональное обсуждение. На этой неделе проходят научно-методические советы по всем учебным предметам. Окончательные демонстрационные варианты будут опубликованы не позднее начала ноября.

Будет ли дистанционная сдача ЕГЭ?

Сейчас действительно существуют пункты проведения экзамена на дому, признал Музаев. Но такой формат предлагается ребятам с ОВЗ, инвалидам. Глава Рособрнадзора отметил, что ЕГЭ пройдет в очной форме: нет технологий для прохождения экзамена дистанционно. Ученики, находящиеся на самоизоляции, смогут пройти тестирование в дополнительные дни.

Когда будем сдавать ЕГЭ на компьютере?

Сейчас компьютеры используются во время экзамена по информатике и устной части ЕГЭ по иностранному языку. Технология такого проведения экзамена, поделился Музаев, была разработана ими как минимум пять лет назад, и ее можно тиражировать на другие предметы. «Но ЕГЭ тогда растянется на месяцы, потому что в единый момент мы не сможем сдавать его: из-за отсутствия необходимого количества оборудования», — констатировал он. При этом чиновник заметил, что поэтапно рано или поздно ряд предметов будет переходить на компьютеры. Но не в ближайшие годы.

Сдавать ЕГЭ в 10 классе не советуется

Фото: Вадим Ахметов © URA.RU

Какой будет пересдача в 2022 году?

Если школьник не сдал экзамены в 2021 году по тем условиям, которые были (из-за COVID), в 2022 году ему придется писать ЕГЭ уже по положению этого года: два обязательных предмета и два по выбору.

Родители также активно интересовались возможностью пересдачи ЕГЭ, если ребенок писал его досрочно — в 10 классе. Для этого требуются удовлетворительные оценки по всем предметам в школе и заявление на досрочную сдачу экзамена — до 1 февраля. Ребенку нужно учиться по индивидуальному плану, освоение которого он должен подтвердить. Но важно понимать, предупредил Музаев, если школьник этот экзамен провалит, он не сможет его пересдать в 11 классе.

Поэтому руководитель Рособрнадзора посоветовал целенаправленно готовиться к экзаменам и спокойно сдавать его в отведенное время. Для тех, кто просто хочет проверить свои силы, можно обратиться в Центры оценки качества образования, которые есть практически во всех субъектах, и написать ЕГЭ там.

Когда будет уточнен формат ГИА?

По словам Музаева, максимум до 1 декабря станет точно известно, сколько экзаменов нужно будет сдавать и в каком формате они будут проводиться.

Подписывайтесь на URA.RU в Google News, Яндекс.Новости и на наш канал в Яндекс.Дзен, следите за главными новостями России и Урала в telegram-канале URA.RU и получайте все самые важные известия с доставкой в вашу почту в нашей ежедневной рассылке.

Единый госэкзамен в 2022 году существенно изменится. Родителям выпускников объяснили, сколько предметов и в каком формате нужно будет сдавать на ЕГЭ и ОГЭ, зачем усложнили математику и обществознание, когда обновится открытый банк заданий ФИПИ и будут ли школьники писать экзамен дистанционно. Об этом — руководитель Рособрнадзора Анзор Музаев и директор Федерального института педагогических измерений Оксана Решетникова. Сколько экзаменов нужно сдавать? Как рассказал руководитель Рособрнадзора Анзор Музаев в рамках Всероссийской онлайн-встречи с родителями, сейчас они отправили на рассмотрение в Минпросвещения РФ предложение вернуться к доковидным порядкам проведения экзаменов. «Объявлять о том, что не будет экзаменов, я не хочу», — подчеркнул чиновник. В частности, речь идет о том, чтобы в 9 классе было два обязательных предмета для сдачи ОГЭ — русский язык и математика — и два по выбору. Точно так же должно быть в ЕГЭ в 11 классе. В том числе Рособрнадзор намерен вернуть в качестве обязательного предмета базовую математику: для тех, кто хочет получить аттестат и не выбирает профильную математику, которая требуется по ряду специальностей. Зачем усложнили математику? В онлайн-встрече с родителями также участвовала директор Федерального института педагогических измерений (ФИПИ, учредитель — Рособрнадзор) Оксана Решетникова. Она помогала с ответами про изменения КИМ (контрольных измерительных материалов) ЕГЭ в 2022 году. К примеру, она объяснила, зачем усложнили экзамен по профильной математике: «Профильная математика избавилась от балласта (заданий, которые выполнялись всеми ребятами), который мало дифференцировал [детей] по уровню подготовленности, мало говорил о том потенциале ребенка, который пригодится в технических, инженерных вузах». При этом, по словам Решетниковой, внеслись задания, дающие ребятам больше возможности проявить себя. Итоговые сочинения проверяют вручную Родители спросили главу Рособрнадзора о том, как оценивается одно из требований итогового сочинения — самостоятельность написания (наличие заимствований — прим. URA.RU). «Проверка — это ручная работа. Программного обеспечения для этого у нас нет. Проверяет эксперт, учитель», — лаконично ответил Музаев. Все одиннадцатиклассники перед экзаменами пишут итоговое сочинение. В этом учебном году оно запланировано на 1 декабря (дополнительные дни — 2 февраля и 4 мая 2022 года). Ранее ученые и репетиторы рассказали URA.RU, как лучше всего готовиться к сочинению и ЕГЭ по русскому языку. Зачем ускорили ЕГЭ по обществознанию? В проекте изменений КИМ единого госэкзамена по обществознанию и истории в 2022 году было обозначено уменьшение времени, данного для ЕГЭ, — с 235 до 180 минут. Как заметила Решетникова, в экзаменах по этим предметам были убраны задания, которые в последние годы сводились к натаскиванию. «Создаются шаблоны, и мы видим несамостоятельные сочинения, которые уже не несут в себе никакого содержательного значения. Мы их изъяли, но именно они были самыми объемными по времени». Кроме того, уточнила она, другие объемные задания были заменены другими, где ответ в разы короче. В октябре в рамках онлайн-консультаций Рособрнадзора руководитель комиссии по разработке КИМ ЕГЭ по обществознанию Татьяна Лискова заявила, что составители экзамена решают, сколько времени все-таки добавить. Появятся ли новые дополнительные предметы? Рособрнадзор постоянно спрашивают, когда и какие предметы станут обязательными наравне с русским языком и математикой. По словам Музаева, каждый пытается выйти с такой инициативой — продвинуть предмет, который любит. «Все предметы важны. Позиция Минпросвещения и наша: та модель, которая существует, — самодостаточна. И мы не планируем вводить дополнительно какой-то обязательный предмет», — успокоил чиновник. Когда обновится открытый банк заданий ФИПИ? Как пояснила директор ФИПИ, с августа идет общественное обсуждение предложенных изменений в ЕГЭ 2022 года. Разработка банка заданий началась одновременно с этим. «В январе мы опубликуем новые задания в банке и обновим навигатор подготовки к ЕГЭ», — заверила Решетникова. Она дополнила, что в каждом КИМе свою форму изменили не более 3-4 заданий. Содержание осталось прежним. До обновления банка Решетникова предложила ознакомиться с форматом заданий в демонстрационном варианте экзамена (выложен на сайте ФИПИ) и начать подготовку к ЕГЭ. По ее словам, сейчас заканчивается общественно-профессиональное обсуждение. На этой неделе проходят научно-методические советы по всем учебным предметам. Окончательные демонстрационные варианты будут опубликованы не позднее начала ноября. Будет ли дистанционная сдача ЕГЭ? Сейчас действительно существуют пункты проведения экзамена на дому, признал Музаев. Но такой формат предлагается ребятам с ОВЗ, инвалидам. Глава Рособрнадзора отметил, что ЕГЭ пройдет в очной форме: нет технологий для прохождения экзамена дистанционно. Ученики, находящиеся на самоизоляции, смогут пройти тестирование в дополнительные дни. Когда будем сдавать ЕГЭ на компьютере? Сейчас компьютеры используются во время экзамена по информатике и устной части ЕГЭ по иностранному языку. Технология такого проведения экзамена, поделился Музаев, была разработана ими как минимум пять лет назад, и ее можно тиражировать на другие предметы. «Но ЕГЭ тогда растянется на месяцы, потому что в единый момент мы не сможем сдавать его: из-за отсутствия необходимого количества оборудования», — констатировал он. При этом чиновник заметил, что поэтапно рано или поздно ряд предметов будет переходить на компьютеры. Но не в ближайшие годы. Какой будет пересдача в 2022 году? Если школьник не сдал экзамены в 2021 году по тем условиям, которые были (из-за COVID), в 2022 году ему придется писать ЕГЭ уже по положению этого года: два обязательных предмета и два по выбору. Родители также активно интересовались возможностью пересдачи ЕГЭ, если ребенок писал его досрочно — в 10 классе. Для этого требуются удовлетворительные оценки по всем предметам в школе и заявление на досрочную сдачу экзамена — до 1 февраля. Ребенку нужно учиться по индивидуальному плану, освоение которого он должен подтвердить. Но важно понимать, предупредил Музаев, если школьник этот экзамен провалит, он не сможет его пересдать в 11 классе. Поэтому руководитель Рособрнадзора посоветовал целенаправленно готовиться к экзаменам и спокойно сдавать его в отведенное время. Для тех, кто просто хочет проверить свои силы, можно обратиться в Центры оценки качества образования, которые есть практически во всех субъектах, и написать ЕГЭ там. Когда будет уточнен формат ГИА? По словам Музаева, максимум до 1 декабря станет точно известно, сколько экзаменов нужно будет сдавать и в каком формате они будут проводиться.

Послабления по ЕГЭ и ОГЭ в 2022 году могут отменить: вернуть базовую математику и все 4 экзамена в 9-х классах

Правда, пока окончательно ничего не известно – Рособрнадзор сообщает, что все решения будут приниматься по ситуации с коронавирусом.

В 2020 и 2021 годах выпускники 9-х и 11-х классов сдавали экзамены в упрощенном порядке. Так, ЕГЭ по базовой математике отменили вообще – выпускник либо сдавал профильную математику для поступления в вуз, либо вообще выбирал более простой государственный выпускной экзамен. В 2020-м вообще отменили ОГЭ для выпускников девятых классов, а в 2021-м его провели в урезанном формате. Учитывая сложную эпидемиологическую ситуацию в стране, многие школьники рассчитывают, что экзамены и дальше будут проходить в упрощенном варианте, однако глава Рособрнадзора Анзор Музаев заявил, что все послабления могут отменить.

Выступая на всероссийской встрече с родителями школьников, Музаев рассказал, как будут проходить экзамены в выпускных классах в 2022 году:

• базовая математика может вернуться – ее будут сдавать те, кто получает аттестат и не выбрал профильную математику для поступления в вуз;
• досрочный период сдачи ЕГЭ могут отменить. Сейчас в приказе говорится о трех периодах: это досрочный период (21 марта – 15 апреля), основной период (27 мая – 2 июля) и дополнительный (5 – 20 сентября). Однако в Рособрнадзоре считают, что досрочный период уже не нужен – его вводили для тех, кто не сможет сдать экзамен в основной период летом, а также для выпускников прошлых лет. Но практика 2020-2021 годов показала, что без досрочного периода можно обойтись;
• основной государственный экзамен для выпускников 9-х классов могут провести в прежнем формате – как это было до пандемии. То есть, это два обязательных предмета (русский язык и математика) и два предмета по выбору. В 2020 году ОГЭ не было вообще, а в 2021-м экзамен был обязательным только по двум предметам, а по двум по выбору школьнику засчитывали результаты контрольной работы.

Таким образом, в 2022 году процедуры сдачи ОГЭ и ЕГЭ уже могут вернуться к нормальному состоянию, какими они были до 2020 года. Правда, сейчас еще есть вопросы со сроками сдачи ЕГЭ – по словам Музаева, они планировались с учетом того, что осенью эпидемиологическая обстановка будет лучше, чем она оказалась по факту. Соответственно, при серьезном росте статистики заболеваемости сроки могут и сдвинуть.

Кроме того, руководитель Рособрнадзора напомнил: ученики 10-х классов могут сдать ЕГЭ досрочно уже в этом году, но только при наличии хотя бы удовлетворительных оценок и с подтверждением от школы (о том, что ученик освоил учебную программу по индивидуальному плану). При этом, если 10-классник провалит экзамен по обязательному предмету, он сможет пересдать его в 11 классе, но пересдать предмет по выбору нельзя.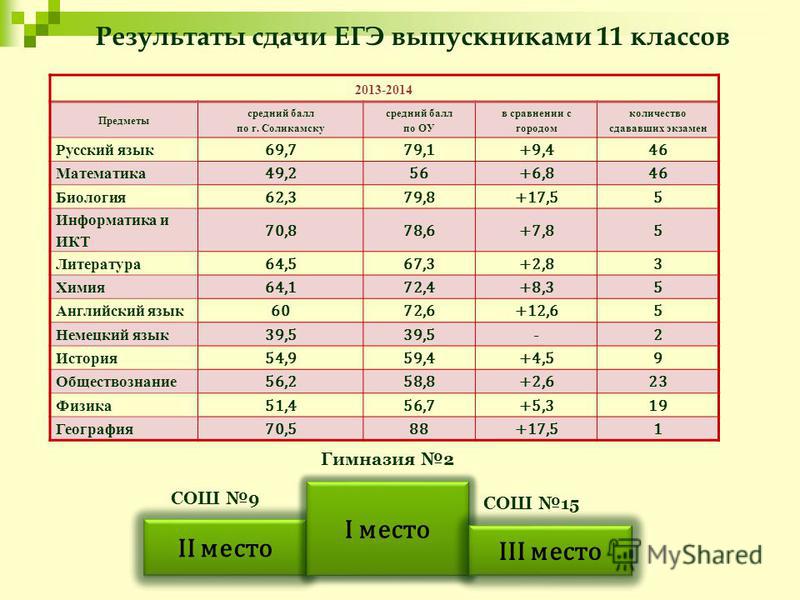

как это будет — Учёба.ру

Чем раньше начнешь готовиться к ЕГЭ,
тем выше будет балл Поможем подготовиться, чтобы сдать экзамены на максимум и поступить в топовые вузы на бюджет. Первый урок бесплатно

Кто сдает ГВЭ?

В 2021 году выпускники школ, которые не планируют поступать в вузы, не сдают ЕГЭ. Для получения аттестата они должны пройти два экзамена — ГВЭ по математике и русскому языку. ГВЭ по русскому языку представляет собой сокращенную версию ЕГЭ по русскому, школьникам предстоит выполнить задания № 1-24. ГВЭ по математике состоит из выборочных заданий ЕГЭ по базовой математике — всего 14 вопросов с кратким ответом.

Расписание ГВЭ

Экзамен будет проводиться в два этапа. Основной этап пройдет 25 мая (русский язык) и 28 мая (математика). В резервные дни 8 и 10 июня смогут написать работу ребята, которые не смогли присутствовать на ГВЭ в основные дни. Дополнительные этапы пройдут в июле и сентябре (13, 17 июля, 3, 6 сентября) для участников, пропустивших экзамены в основной период по уважительной причине или получивших «двойку».

25 мая	русский язык
28 мая	математика
8, 10 июня	резервные дни

*Проект расписания ГВЭ от 5 февраля 2021 года.

Кто сдает ЕГЭ?

ЕГЭ сдают только выпускники, поступающие в вузы. Всего экзамен проводится по 15 предметам. Все абитуриенты сдают ЕГЭ по русскому языку, а также два-три ЕГЭ по выбору в зависимости от перечня предметов, необходимых для поступления на одно или несколько желаемых направлений. Выбрать можно любое количество дисциплин. Заявление об участии в ЕГЭ со списком предметов подается до 1 февраля.

В качестве допуска к ЕГЭ школьники должны написать итоговое сочинение, которое пройдет 15 апреля, 5 и 19 мая.

Для получения аттестата выпускникам, поступающим в вузы, достаточно сдать на удовлетворительный результат ЕГЭ по русскому языку. ЕГЭ по математике базового уровня в 2021 году проводиться не будет.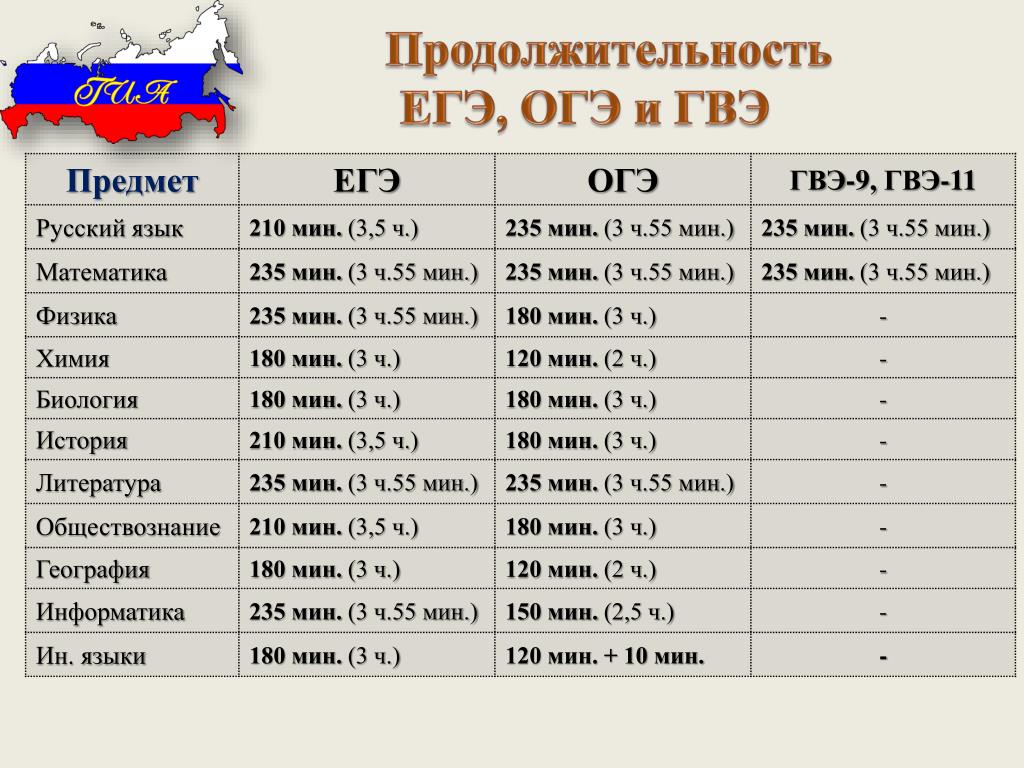

Расписание ЕГЭ

В 2021 году ЕГЭ будет проводиться в два этапа. Основной этап пройдет с 31 мая по 25 июня. Резервные дни (с 28 июня по 2 июля) предусмотрены в расписании для тех, у кого экзамены по предметам совпали в один день, и для тех, кто пропустил экзамен в основной день по болезни. Дополнительный этап пройдет с 12 по 17 июля для выпускников, не сдавших экзамен в основной день по уважительной причине.

Досрочный период ЕГЭ в этом году отменен, а выпускники прошлых лет смогут сдать экзамены в основные дни основного периода.

*Проект расписания ЕГЭ от 5 февраля 2021 года.

Основание для получения аттестата

Выпускники школ, не поступающие в вузы	Выпускники школ, поступающие в вузы
ГВЭ по русскому языку ГВЭ по математике	ЕГЭ по русскому языку (минимум 24 балла)

Пересдачи ГВЭ

Если школьник получил неудовлетворительную оценку на ГВЭ по математике и/или русскому языку, у него будет возможность пересдать эти экзамены в дополнительные сроки (3, 6 сентября) и получить аттестат.

Пересдачи ЕГЭ

В текущем учебном году пересдать ЕГЭ могут только школьники, получившие неудовлетворительную оценку по русскому языку. Если выпускник не преодолел минимальный порог по русскому, он имеет право пересдать экзамен в дополнительный период, поскольку результат этого ЕГЭ служит основанием для получения аттестата.

В случае, если участник ЕГЭ не получает минимального количества баллов по другим предметам или просто хочет улучшить свой результат, пересдать экзамен он может только через год.

Можно ли изменить форму сдачи экзамена с ЕГЭ на ГВЭ и наоборот?

Выпускники могут передумать и изменить форму прохождения государственной итоговой аттестации по заявлению. Решение принимает региональная государственная экзаменационная комиссия (ГЭК). Предполагается, что заявления с указанием изменения формы экзамена могут подаваться в ГЭК не позднее, чем за две недели до даты первого экзамена основного периода.

Экзамены для абитуриентов колледжей

Выпускники школ, которые планируют поступать в колледж, должны сдать ГВЭ по математике и русскому языку для получения аттестата. После этого они подают заявление в колледж и участвуют в конкурсе на основании среднего балла аттестата.

Чем раньше начнешь готовиться к ЕГЭ,
тем выше будет балл Поможем подготовиться, чтобы сдать экзамены на максимум и поступить в топовые вузы на бюджет. Первый урок бесплатно

Удачной сдачи ЕГЭ пожелал Михаил Дегтярев одиннадцатиклассникам

Михаил Дегтярев проверил сегодня, как организованы единые государственные экзамены в регионе. Он побывал в ППЭ на базе 6-й гимназии, где в течение 3 часов 55 минут 71 человек сдает ЕГЭ по физике.

– Уверен, что каждый из вас приложил максимум усилий для того, чтобы сдать ЕГЭ с наилучшим результатом, ведь от этого зависит ваша дальнейшая судьба, – сказал, обращаясь к одиннадцатиклассникам, врио губернатора. – Вы молодые, умные и энергичные. Перед вами открыты все дороги. Важно, чтобы вы знали: куда бы вас ни забросила судьба и как бы далеко вы не были, вы очень нужны
в нашем родном крае.

В этом году ЕГЭ проходит с некоторыми особенностями. Для выпускников 11-х классов и других экзаменующихся досрочный период проведения экзаменов в связи с текущей эпидемиологической обстановкой в 2021 году отменен. Для получения аттестата о среднем общем образовании выпускники, которые не планируют поступать в вузы, вместо ЕГЭ сдавали государственный выпускной экзамен (ГВЭ) по двум предметам – русскому языку и математике. Выпускникам, которые собираются поступать в вузы и сдают для этого ЕГЭ, чтобы получить аттестат, достаточно сдать на удовлетворительный результат ЕГЭ по русскому языку. ЕГЭ по математике базового уровня в 2021 году не проводится.

Для участников ЕГЭ, которые не смогут сдать экзамены в основные сроки по болезни или иной уважительной причине, предусмотрен дополнительный период в середине июля 2021 года. Эти сроки увязаны с графиком приемной кампании в вузы – все, кто будет сдавать ЕГЭ в дополнительный период, так же, как и участники основного периода, успеют получить свои результаты и подать документы в выбранные учебные заведения.

В 2021 единые госэкзамены в Хабаровском крае сдают 6 290 человек. Из них выпускники текущего года – 5 689 человек, выпускники прошлых лет – 571 человек, студенты СПО – 29 человек. Также на сдачу ЕГЭ зарегистрирован один учащийся 10 класса.

Пресс-служба губернатора и правительства Хабаровского края
При использовании материалов ссылка на сайт www.khabkrai.ru обязательна

Стандартов для математической практики | Инициатива Common Core State Standards

Стандарты математической практики описывают различные виды знаний, которые преподаватели математики на всех уровнях должны стремиться развивать у своих учеников. Эти методы основаны на важных «процессах и умениях», которые имеют давнюю важность в математическом образовании. Первыми из них являются стандарты процесса NCTM для решения проблем, обоснования и доказательства, коммуникации, представления и связей.Вторые – это направления математической подготовки, указанные в отчете Национального исследовательского совета Adding It Up : адаптивное мышление, стратегическая компетентность, концептуальное понимание (понимание математических концепций, операций и отношений), беглость процедур (умение гибко выполнять процедуры, точно, эффективно и уместно) и продуктивному расположению (привычная склонность считать математику разумной, полезной и стоящей, в сочетании с верой в усердие и собственную эффективность).

Стандарты в этой области:

CCSS.Math.Practice.MP1 Разбирайтесь в проблемах и настойчиво их решайте.

Учащиеся со знанием математики начинают с объяснения себе значения проблемы и поиска точек входа для ее решения. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто предпринимают попытки решения. Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной проблемы, чтобы получить представление о ее решении.Они отслеживают и оценивают свой прогресс и при необходимости меняют курс. Старшие ученики могут, в зависимости от контекста задачи, преобразовывать алгебраические выражения или изменять окно просмотра на своем графическом калькуляторе, чтобы получить необходимую информацию. Математически опытные студенты могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и отношений, графических данных и искать закономерности или тенденции. Младшие ученики могут полагаться на использование конкретных предметов или изображений, чтобы помочь осмыслить и решить проблему.Математически опытные ученики проверяют свои ответы на задачи, используя другой метод, и они постоянно спрашивают себя: «Имеет ли это смысл?» Они могут понимать подходы других к решению сложных проблем и определять соответствия между разными подходами.

CCSS.Math.Practice.MP2 Размышляйте абстрактно и количественно.

Учащиеся со знанием математики понимают величины и их отношения в проблемных ситуациях. Они привносят две взаимодополняющие способности для решения проблем, связанных с количественными отношениями: способность деконтекстуализировать – абстрагировать данную ситуацию и представлять ее символически и манипулировать символами представления, как если бы они жили своей собственной жизнью, не обязательно обращая внимание на своих референтов. – и возможность контекстуализировать , останавливаться по мере необходимости во время процесса манипуляции, чтобы исследовать референты для задействованных символов. Количественное мышление подразумевает привычку создавать связное представление о проблеме; с учетом задействованных единиц; внимание к значению количеств, а не только к тому, как их вычислить; знание и гибкое использование различных свойств операций и объектов.

CCSS.Math.Practice.MP3 Создавайте жизнеспособные аргументы и критикуйте рассуждения других.

Студенты со знанием математики понимают и используют заявленные предположения, определения и ранее установленные результаты при построении аргументов.Они делают предположения и выстраивают логическую последовательность утверждений, чтобы исследовать истинность своих предположений. Они умеют анализировать ситуации, разбивая их на случаи, а также могут распознавать и использовать контрпримеры. Они оправдывают свои выводы, сообщают их другим и отвечают на аргументы других. Они индуктивно рассуждают о данных, приводя правдоподобные аргументы, которые принимают во внимание контекст, из которого эти данные возникли. Математически опытные учащиеся также могут сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и – если в аргументе есть изъян – объяснять, что это такое. Учащиеся начальной школы могут строить аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не принимаются формально до более поздних оценок. Позже студенты учатся определять области, к которым применим аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.

CCSS. Математика. Практика.Модель MP4 с математикой.

Учащиеся со знанием математики могут применять полученные знания для решения задач, возникающих в повседневной жизни, в обществе и на рабочем месте. В младших классах это может быть так же просто, как написать дополнительное уравнение для описания ситуации. В средних классах ученик может применять пропорциональное рассуждение для планирования школьного мероприятия или анализа проблемы в сообществе. В старшей школе ученик может использовать геометрию для решения проектной задачи или использовать функцию, чтобы описать, как одна интересующая величина зависит от другой. Математически опытные студенты, которые могут применять то, что они знают, комфортно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что они могут потребовать пересмотра позже. Они могут определять важные величины в практической ситуации и отображать свои отношения с помощью таких инструментов, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически проанализировать эти отношения, чтобы сделать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не служит своей цели.

CCSS.Math.Practice.MP5 Стратегически используйте соответствующие инструменты.

Студенты, разбирающиеся в математике, рассматривают доступные инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии. Опытные студенты в достаточной степени знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезен, признавая как понимание, которое необходимо получить, так и их ограничения.Например, старшеклассники со знанием математики анализируют графики функций и решений, сгенерированные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценки и другие математические знания. Создавая математические модели, они знают, что технологии могут позволить им визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Учащиеся с математическими знаниями в различных классах могут определять соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач.Они могут использовать технологические инструменты для изучения и углубления понимания концепций.

CCSS.Math.Practice.MP6 Внимание к точности.

Учащиеся со знанием математики стараются точно общаться с другими. Они пытаются использовать четкие определения в обсуждениях с другими и в своих собственных рассуждениях. Они заявляют значение выбранных символов, в том числе используют знак равенства последовательно и надлежащим образом. Они осторожны при указании единиц измерения и маркировке осей, чтобы уточнить соответствие количеству в проблеме.Они производят точные и эффективные вычисления, выражают числовые ответы со степенью точности, соответствующей контексту проблемы. В начальных классах ученики дают друг другу тщательно сформулированные объяснения. К моменту поступления в среднюю школу они научились проверять утверждения и четко использовать определения.

CCSS.Math.Practice.MP7 Ищите и используйте структуру.

Студенты, разбирающиеся в математике, внимательно приглядываются, чтобы различить образец или структуру. Молодые студенты, например, могут заметить, что три и семь больше равны семи и еще трём, или они могут отсортировать набор фигур в зависимости от того, сколько сторон у этих фигур. Позже учащиеся увидят, что 7 × 8 равно хорошо запоминающимся 7 × 5 + 7 × 3, при подготовке к изучению свойства распределения. В выражении x ² + 9 x + 14 старшие ученики могут видеть 14 как 2 × 7 и 9 как 2 + 7. Они осознают значение существующей линии в геометрической фигуре и могут использовать стратегия проведения вспомогательной линии для решения задач. Они также могут сделать шаг назад для обзора и изменения перспективы. Они могут видеть сложные вещи, такие как некоторые алгебраические выражения, как отдельные объекты или как составленные из нескольких объектов.Например, они могут видеть 5 – 3 ( x – y ) ² как 5 минус положительное число, умноженное на квадрат, и использовать это, чтобы понять, что его значение не может быть больше 5 для любых действительных чисел x и и .

CCSS.Math.Practice.MP8 Ищите и выражайте закономерность в повторяющихся рассуждениях.

Студенты, разбирающиеся в математике, замечают, если вычисления повторяются, и ищут как общие методы, так и ярлыки. Ученики старших классов могут заметить при делении 25 на 11, что они повторяют одни и те же вычисления снова и снова, и прийти к выводу, что у них есть повторяющаяся десятичная дробь.Обращая внимание на расчет наклона, поскольку они неоднократно проверяют, находятся ли точки на прямой, проходящей через (1, 2) с наклоном 3, ученики средней школы могут абстрагироваться от уравнения ( y – 2) / ( x – 1) = 3. Обратите внимание на закономерность в том, как условия отменяются при раскрытии ( x – 1) ( x + 1), ( x – 1) ( x ² + x + 1), и ( x – 1) ( x ³ + x 2 + x + 1) может привести их к общей формуле для суммы геометрического ряда.Решая задачу, учащиеся с математическими знаниями следят за процессом, уделяя внимание деталям. Они постоянно оценивают разумность своих промежуточных результатов.

Соединение стандартов математической практики со стандартами математического содержания

Стандарты математической практики описывают способы, с помощью которых развивающиеся студенты, практикующие математическую дисциплину, должны все больше вовлекаться в предмет по мере того, как они растут в математической зрелости и опыте на протяжении младших, средних и старших классов школы. Разработчики учебных программ, оценивания и повышения квалификации должны уделять внимание необходимости увязать математические практики с математическим содержанием в обучении по математике.

Стандарты математического содержания представляют собой сбалансированное сочетание процедуры и понимания. Ожидания, начинающиеся со слова «понять», часто являются особенно хорошей возможностью связать практики с содержанием. Студенты, которым не хватает понимания темы, могут слишком сильно полагаться на процедуры.Без гибкой основы для работы они с меньшей вероятностью будут рассматривать аналогичные проблемы, связно представлять проблемы, обосновывать выводы, применять математику к практическим ситуациям, осознанно использовать технологии для работы с математикой, точно объяснять математику другим ученикам, сделайте шаг назад, чтобы получить обзор, или отклонитесь от известной процедуры, чтобы найти ярлык. Короче говоря, непонимание фактически мешает студенту заниматься математической практикой.

В этом отношении те стандарты содержания, которые устанавливают ожидания понимания, являются потенциальными «точками пересечения» между Стандартами математического содержания и Стандартами математической практики.Эти точки пересечения призваны соотносить с центральными и генеративными концепциями школьной программы математики, которые в наибольшей степени заслуживают времени, ресурсов, инновационной энергии и сосредоточенности, необходимых для качественного улучшения учебной программы, обучения, оценивания, профессионального развития и успеваемости учащихся в школе. математика.

стандартов по математике | Common Core State Standards Initiative

В течение более чем десяти лет исследования математического образования в высокоэффективных странах пришли к выводу, что математическое образование в Соединенных Штатах должно стать значительно более целенаправленным и последовательным, чтобы улучшить успеваемость по математике в этой стране.Чтобы выполнить это обещание, стандарты математики предназначены для решения проблемы учебной программы, которая «имеет ширину в милю и глубину в дюйм».

Эти новые стандарты основаны на лучших из высококачественных математических стандартов разных штатов страны. Они также опираются на наиболее важные международные модели математической практики, а также исследования и информацию из многочисленных источников, включая государственные департаменты образования, ученых, разработчиков оценок, профессиональные организации, преподавателей, родителей и студентов, а также представителей общественности.

Математические стандарты обеспечивают ясность и конкретность, а не общие общие положения. Они стремятся следовать замыслу, предложенному Уильямом Шмидтом и Ричардом Хоуангом (2002), не только подчеркивая концептуальное понимание ключевых идей, но и постоянно возвращаясь к организационным принципам, таким как числовая стоимость и законы арифметики, для структурирования этих идей.

Кроме того, «последовательность тем и представлений», описанная в своде математических стандартов, должна соответствовать тому, что уже известно о том, как учащиеся учатся. Как отмечает Конфри (2007), разработка «последовательных препятствий и проблем для учащихся… без понимания смысла, вытекающего из тщательного изучения обучения, было бы неудачным и неразумным». Таким образом, разработка стандартов началась с основанных на исследованиях последовательностей обучения, детализирующих то, что известно сегодня о том, как со временем развиваются математические знания, навыки и понимание учащихся. Знания и навыки, которые необходимо подготовить учащимся для изучения математики в колледже, карьере и жизни, вплетены в стандарты математики.Они не включают отдельные стандарты привязки, подобные тем, которые используются в стандартах ELA / грамотности.

Common Core концентрируется на четком наборе математических навыков и концепций. Учащиеся будут изучать концепции более организованным образом как в течение учебного года, так и между классами. Стандарты побуждают студентов решать реальные проблемы.

Понимание математики

Эти стандарты определяют, что учащиеся должны понимать и уметь делать при изучении математики. Но просить ученика что-то понять также означает просить учителя оценить, понял ли ученик. Но как выглядит математическое понимание? Один из способов сделать это для учителей – попросить ученика обосновать, в соответствии с математической зрелостью ученика, почему конкретное математическое утверждение истинно или откуда взялось математическое правило. Математическое понимание и процедурные навыки одинаково важны, и оба они поддаются оценке с помощью математических задач достаточного разнообразия.

ТЕХАСКАЯ ИНИЦИАТИВНАЯ ОЦЕНКА УСПЕХА 2.0 Примеры вопросов по математике

% PDF-1.4 % 1 0 объект / Producer (Adobe PDF Library 15.0) / Title (TEXAS SUCCESS INITIATIVE ASSESSMENT 2.0 Примеры вопросов по математике) / Trapped / Unknown >> эндобдж 2 0 obj / MarkInfo 7 0 R / Метаданные 8 0 R / Имена 9 0 R / OpenAction 275 0 R / Контуры 276 0 R / PageLabels 908 0 R / PageLayout / SinglePage / Pages 13 0 R / StructTreeRoot 871 0 R / Тип / Каталог / ViewerPreferences >>> эндобдж 3 0 obj > / Шрифт >>> / Поля [] >> эндобдж 4 0 объект > эндобдж 5 0 объект > эндобдж 6 0 объект > эндобдж 7 0 объект > эндобдж 8 0 объект > поток 3SZfT1uVKS8BEwZpbsDNL32020-08-25T10: 44: 16 + 05: 302020-09-11T17: 24: 31 + 05: 302020-09-11T17: 24: 31 + 05: 30Adobe InDesign CC 13. 1 (Macintosh) uuid: 4a96b24f-9028-491d-b897-311e9fb04629adobe: docid: indd: 3e55a07c-90b9-11da-be4c-f9c4cf49cb59xmp.id: 72abcc23-e0d8-4f669xmp.id: 72abcc23-e0d8-4f66aiddf21cdfc: f0d8-4f66a2df2-22fcd2ddddddddddddddddddddddddddddddddddddddddddddd-fcd-fc-dd-dd-fd-dd-fd-fcd-fd-dd-fd-dd-fd-dd-dd-dd-dd-dd-dd-d1-d4-dd-d4-d4- …-p ,-p.p. 41e9-9407-3b491aea0bafxmp.did: 1dc7c3f1-564a-4058-8f93-6d4e79c6507cadobe: docid: indd: 3e55a07c-90b9-11da-be4c-f9c4cf49cb59default

-приложение CCB59 / 2020, преобразованное из приложения MacDesign в CC / 2020; -08-25T10: 44: 16 + 05: 30

application / pdf

ОЦЕНКА УСПЕХА ТЕХАСА 2.0 Примеры вопросов по математике

Библиотека Adobe PDF 15.0Unknown1

PDF / UA Универсальная схема доступности http://www.aiim.org/pdfua/ns/id/pdfuaid

partIntegerinternalIndicates, которая соответствует стандарту ISO 14289

конечный поток эндобдж 9 0 объект > эндобдж 10 0 объект > эндобдж 11 0 объект > / Font> / ProcSet [/ PDF / Text] / XObject >>> / Rotate 0 / StructParents 2 / Tabs / S / TrimBox [0 0 612 792] / Type / Page >> эндобдж 12 0 объект > поток HWrH} Giɹ (3ai & elj6977I; XL {~ jv19bo? EOqF Dmie | 1jfôK ^ & [c΅ ~ 2!} Mkz> ~ y` * A / Pl | q7LH \ 2K ItNwyєeeϹ? @ KEU6, + ZtG7y! x) YvDr] 򊶗؇? IGo9 “ǥHH-5YҔR {? YmixkNun` {N = M @ & c0e * ˊ * AE8Ki

Алгебра 1 модуль 3 тестовые ответы

алгебра 1 модуль 3 тестовые ответы Изучайте словарный запас, термины и многое другое с помощью карточек, игр и других средств обучения. 13. Kost II 2014-03 В этой книге рассматриваются необходимые концепции, которые появляются на экзамене по пенсильванской алгебре I Keystone – модуль 1. модуль 3 по алгебре 1 тестовые flvs, flvs модуль 3 карточки и учебные наборы викторины, модуль 3 ресурсы виртуальной школы, модуль flvs по алгебре 1 9 ответов zomt com au, flvs algebra 1 модуль 6 ответов partygorilla com, dba questions algebra 2, flvs флорида виртуальная школа классы k 12 онлайн, преодоление страха перед dbas виртуальный голос, flvs holt mcdougal algebra 1 урок 3-2 отношения и функции ответы / вопросы и ответы на экзамен по калифорнии dmv / стоимость экзамена cna / смешные ответы на экзамен facebook iq / ответы на базовый экзамен bloomberg / ответы на сертификационный экзамен bloomberg, вашингтон / 2021 год, экзамен AP Calculus ab по практическому экзамену / edgenuity geometry совокупный экзамен / экзамен по английскому языку vcaa 2021 / ssc je ответ ключ / gcse вопросы по математике и алгебре 1 алгебра 1 практический тест ответ на листе для ответов. Урок 3. 3 5. ответы zomt com au, flvs сегмент 1 обзор и практический тест, скачать flvs algebra 2 модуль 6 ответ pdf, flvs 03 09 модуль 3 обзор и практический тест ответы, преодоление страха перед dbas виртуальный голос, flvs модуль геометрии 3 отвечает на экзамен net, flvs algebra 1 модуль 6 dba отвечает ciecalculator com, выполнил ли кто-нибудь алгебру 2 Алгебра 1 Задания – миссис а. отражается по оси x, уменьшено на 2, вправо 3, вверх 3. H 5. J 9. 2. 1 Упростите / оцените выражения, включающие предварительный тест для диагностики алгебры 50 вопросов – 60 минут Множественный выбор Используйте ответ «NOTA» (который стоит для None of the Above), если ответ не указан 1.3 # 1-18 все 5. Это видео включает и рассматривает материалы курса FLVS Algebra 1. Глава 1 – Ответы на вещественные числа Глава 2 Глава 2 – Линейные уравнения и неравенства в одной переменной 24 апреля 2021 г. · Майк получает ровно 8 правильных ответов. Engage NY Eureka Math Algebra 2 Модуль 1 Урок 3 Ключевые ответы Eureka Math Algebra 2 Модуль 1 Урок 3 Вводное упражнение Ключевые слова. варианты ответа. Экзамены с показанными решениями и работами; Интегрированные обзорные листы алгебры по темам; Стандартизированная практика тестирования; Алгебра 26 февраля 2021 г. · 2 класс, модуль 3, уроки 1-21 Eureka Math, ответ – 423.Вычислите 7m + 3mn, когда m = 8 и n = 14 A) 84 B) 196 C) 392 D) 168 E) NOTA 2. x = 5 B. АЛГЕБРА 1. Возможные ответы: Правильный ответ: Объяснение: Когда мы множим на множители, мы не забудьте проверить знаки в трехчлене. День 3 – Введение в проценты – Заметки – Видео HW – Процентные пропорции День 4 – Процент проблем – Заметки – Видео HW – Процент приложений День 5 – Тест (дни 1–4) День 6 – Обзор теста модуля 3 – Учебное пособие по модулю 3 – Ответить на ключевые видеоролики: Коэффициенты и ставки День 7 – Модуль 3 Тестовые дни 8 и 9 – Модуль 3 Завершающее задание ВИКТОРИНА 3.48 терминов. Колледж Расмуссена. Миссис Адодд. Антропология (9929) Биология (1516) Бизнес (23373) Химия (2281) Коммуникация (1872) Компьютер (24036) Экономика (6122) Образование (4215) Модуль 1. наклон: 1, точка пересечения по оси Y: 10 a. 5 Глава 2. Практический тест №1 по алгебре EOC. y = -2 I x – 3 I + 3. Преобразуем 7 8 в десятичную форму. 7 рациональных выражений и уравнений; 1. A. Для пунктов с множественным выбором обведите правильный ответ. 12 октября 2021 г. · Проверьте 33+ страницы алгебры 1, тестовые отношения блока 3 и функции, отвечающие на ключевой анализ в формате Google Sheet.3 Просмотрите рабочий лист 7 22 сентября Модуль 3 ТЕСТ Модуль 3 Алгебра 1 Модуль 5 День Дата Раздел Примечания Задание Ответы 1 25 сентября 5. Нет Нарисуйте на графике каждое соотношение или уравнение и найдите область и диапазон. Эшли_Пинеда 52. Дата: 1 декабря 2021 г. | Размер: 19. [48] 1 В школьном книжном магазине карандаш стоит 25 ¢, 3! R Алгебра I – Практический экзамен Студент, переписанное выражение Хосе x (x2 + 4x – 12) 4 июня 2019 г. · Свободная алгебра 1 Вопросы для практического теста . Холт Алгебра 1 ответы Глава 6 – экзамен. Вы также можете распечатать практические вопросы, проработать их и поместить в свои заметки для использования на экзамене по модулю 1. Каждый ответ показывает, как решить задачу из учебника, шаг за шагом. Алгебра I: выпускной экзамен в средней школе Пройдите этот практический тест, чтобы проверить свои знания материала курса. Тест в понедельник, 9 ноября 2015 г. G 7. Учебное пособие по алгебре 1 с ответами, обзор теста по главе 1 по алгебре 2, по алгебре 1, оценка ресурсов по методам задач, учебное пособие для родителей и учащихся, обзор экзамена. 1 5. y 6 3 5 (x 2) 17. 14) Инструкции по использованию онлайн-плана обучения для повышения уровня знаний (стр. 2020 Regents Exam Review) Часть 1 Алгебра 1 Практика EOC Флорида ЭТИ ПРИЛОЖЕНИЯ СДЕЛАЮТ ВАШУ ДОМАШНЮЮ РАБОТУ ЗА ВАС !!! ПОЛУЧИТЕ ИХ СЕЙЧАС / КЛЮЧИ ОТВЕТА ДЛЯ ДОМАШНЕГО ЗАДАНИЯ / БЕСПЛАТНЫЕ ПРИЛОЖЕНИЯ. 5 B 30 C 6 D 31 C 7 A 32 B 8 E 33 E 9 C 34 C 10 B 35 A 11 A 36 E 12 C 37 B 13 A 38 A 14 E 39 A 15 E Экспресс-тренинг по алгебре I Keystone Exam Exam – модуль 1-Чарльз П.2 примечания 5. 3 примечания 5. G Алгебра 2 вопроса, получить решение сейчас, Алгебра 2 саксон, бесплатные загрузки уравнений с дробями, замена в алгебре, кто изобрел алгебру, бесплатные контрольные работы по математике. В Модуле 1 8-го класса учащиеся расширяют свои базовые знания о положительных целочисленных показателях и доказывают законы экспонент для любого целочисленного показателя. Алгебра I Модуль 3: Линейные и экспоненциальные функции. Тест lynns в социальных сетях 1. Практический экзамен по алгебре в колледже KYOTE1 1. Если 320 человек – мальчики, то сколько девочек? A 432 девочки B 320 девочек C 256 девочек D 144 девочки Группа Количество Млекопитающие, Рептилии, 13 644 Амфибии Птицы 9 000 Рыбы 22 000 Растений 443 644 Беспозвоночные 4 400 000 Практические ответы: 1.Если вы сдадите Алгебру 1 за седьмой, запишите каждую фразу в виде математического выражения. A 4. Eureka Math ™ Algebra I, модуль 1, 2016 г. Издание для учителей Опубликовано G. org 10 9 8 7 6 5 4 3 2 Alg I-M1-TE-1. 01 Справочное видео по GCF Экзамен по алгебре I Keystone состоит из экзаменационных вопросов, сгруппированных в два модуля: Модуль 1 – Операции, линейные уравнения и неравенства и Модуль 2 – Линейные функции и организация данных. 1 – 3. Наши совершенно бесплатные практические тесты по Алгебре 1 – идеальный способ улучшить свои навыки.Вопрос по алгебре 2, получить решение сейчас, саксон по алгебре 2, бесплатные загрузки уравнений с дробями, подстановка в алгебре, кто изобрел алгебру, бесплатные контрольные работы по математике. 1-10. Математика Eureka 7 класс, модуль 3, урок 4, основные ответы. Результаты учащихся. Учащиеся используют модель площади для написания продуктов как продуктов. два модуля: Модуль 1 – Операции и линейные уравнения и неравенства и Модуль 2 – Линейные функции и организации данных. f (x) = x + 3. Модуль 01 Оценка_ Попытка обзора. MATH 1222 – Зима 2016.Де Холт Макдугал Координатная алгебра Линейные и экспоненциальные функции Ответы (продолжение) Модуль 11 Тест 1. x = -5 2. отражение по оси x, растянутое на 2, вправо на 3, вверх 3. вертикальный сдвиг вниз на 11 единиц Модуль 12 Тест 1. Алгебра 1A Глава 3. Начните изучать лексику раздела 1 алгебры Nation. 4 ключ ответа. Ответ: A (n) = (\ (\ frac {1} {4} \)) n. Предварительный тест для диагностики алгебры C 50 вопросов – 60 минут Множественный выбор Используйте ответ «NOTA» (что означает «Ничего из вышеперечисленного»), если ответа нет в списке 1.J 3. Просмотр подготовки к экзамену – Алгебра 1 – Блок 1 – ПРАКТИКА – Тест – 2017 – КЛЮЧ. B 8. 9 часов назад Эту книгу можно купить у издателя на сайте eureka-math. Какая система уравнений изображена на графике? A. 9 Пересмотрите Alg B. 2–3. 17 октября 2021 г. · Вы можете прочитать 28+ страниц с анализом ответов на тест по алгебре 1, блок 3, анализ ответов в формате Google Sheet. oneself”Flvs Algebra 1 Module 3 Test Answers paperboxbooks com 26 апреля 2018 – Читать документ онлайн 2018 Flvs Algebra 1 Module 3 Test Answers Этот PDF-файл состоит из Flvs Algebra 1 Module 3 Test Answers, чтобы загрузить этот файл данных, вы должны подписать ” ответы на экзамен 03 09 модуль три обзор и практика видео модуль словаря 3 3 00 часть 1 3 00 часть 2 3 01 flvs 03 09 модуль третий обзор и практика тест ответы модуль геометрии, вот лучший ресурс для домашних заданий помощь по алгебре алгебра 2 в виртуальной средней школе Флориды найти алгебру 2 учебные пособия заметки и практика flvs сегмент алгебры Алгебра 1 Имя _____ © t X290 1Q3r 8Kju TtGaP ZSZoXfjt swDa Zrze b PLCLqCk. Вместо этого используйте свои неправильные ответы для определения конкретных областей в онлайн-плане обучения. x-3 + 2×2 – 7 x3 + 2×2 – 7 3. 2 (I) F 3 2 Готовность A. Алгебра 1 Глава 1 Обзор теста и Глава 1 Информация о тесте Информация о тесте • 32 вопроса с короткими ответами (вопросы такого же типа, как показано на оба обзора теста) • Возможное общее количество баллов – 100 баллов • 4 балла можно указать за то, что ваше имя и точка будут указаны как на листе для ответов, так и на листе теста. В математике алгебра играет очень важную роль. Формула расстояния.Это первая глава в алгебре Гленко 1. 1 Алгебра Холта Макдугала 1 глава 3 тестовые ответы. g (x) 3x 2 18. Математика 7 класс Модуль 1: Соотношения и пропорциональные отношения. Примечания к классу: 3. f (x 7) 19. Рабочие листы Free Algebra 1, созданные с помощью Infinite Algebra 1. 3 страницы. Чтобы помочь проверить ваши ответы: 3. 2x + 1 1 2 x 2. com Отображение 8 лучших заданий, найденных для – Алгебра Холта 1 правильные ответы на тесте 2021 года (1) Алгебра 1 Практика заключительного экзамена (январь 300 секунд. Зарегистрируйтесь сейчас. К ним прилагается этот тестовый модуль 2c по алгебре glencoe 2 глава 1 ответы, которые могут быть вашим партнером.D 10. 14. Трамплин курс математики 1 блок 1 тест Трамплин курс математики 1 блок 1 тест Алгебра 1 том 2 модуль 15 – катыкрамер. Оценка основывается на полноте их работы, включая отображение всей работы и доказательств исправления 27 января 2020 г. · Общие основные ответы по алгебре 1 ISBN: 9780133185485 Практика и решение проблем Рабочая тетрадь Алгебра 1 Общие основные ответы Глава 1 Основы алгебры Глава 1 Глава 1 16) Инструкции: примите это как тест без какой-либо помощи или каких-либо заметок.А1. Алгебра 1 Практический тест в конце курса с решениями. 1. 3 Глава 1. Защита от дурака, модуль 8, ответы Quizlet. Уравнение круга. Урок 2 Ключевые ответы ОБЩАЯ УЧЕБНАЯ ЗАПИСЬ ПО МАТЕМАТИКЕ NYS 4 3 Модуль 3. 1 Операции с действительными числами и выражениями Дескриптор привязки Допустимое содержимое Расширенный стандарт A1. Джордж разрезал 2 3 части пирога и положил этот гигантский кусок на тарелку. 4 26 февраля 2021 г. · 2 класс, модуль 3, уроки 1–21 Eureka Math, ответ – 423. b. . Пройдите один из наших многочисленных практических тестов по Алгебре 1, чтобы получить ответы на часто задаваемые вопросы.Функции и отношения. B 6. Правила выполнения домашних заданий: ученые должны показать всю работу на отдельном листе бумаги. HMH Алгебра 1 класс 8 учебное пособие и ответы онлайн. 2 Введение в функции; 2. В младших классах учащиеся определяют: Алгебра I Модуль 3: Упрощенный китайский – Zip-папка с файлами PDF (4. Плюс к каждому из них есть ключ ответа. Майк получает не более 3 правильных ответов. 2 ответа 3 9/27 5. Разделите член x на сумму двух членов, разложите на множители каждую часть выражения отдельно, а затем вычтите GCF всего выражения.3 Глава 2. Если f (x) = √ 7 −x, то какое из следующих множеств является областью определения этой функции? . Бесплатные распечатываемые рабочие листы функций (pdf) с ключами ответов в домене / диапазоне, оценочными функциями, составом функций, 1 к 1 и т.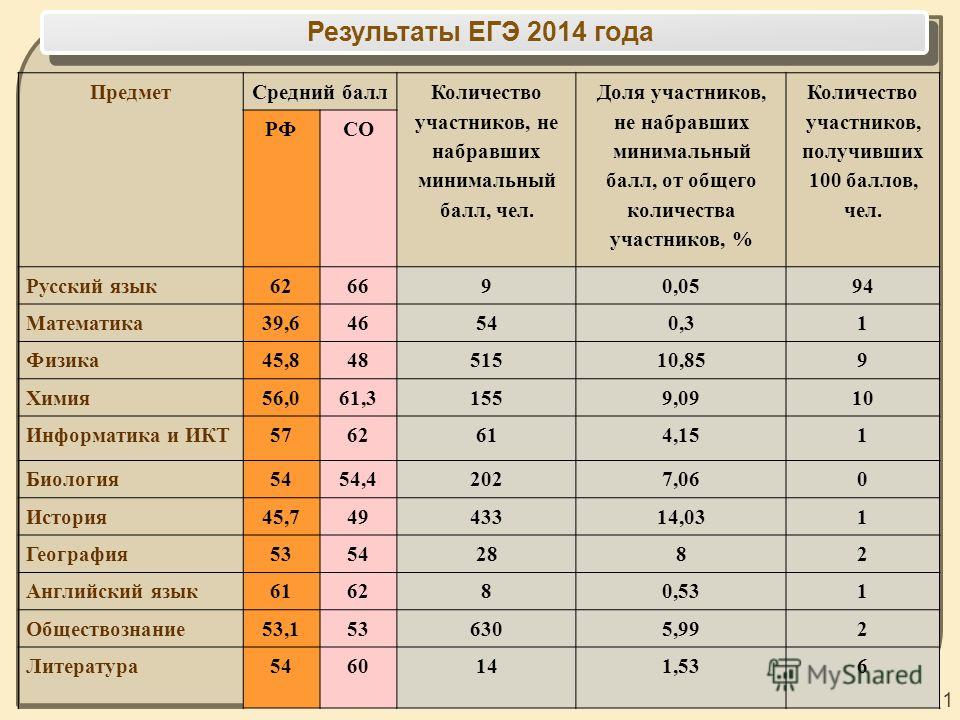 Д. Используйте код скидки 20%: PRETECH, чтобы получить отремонтированную бывшую в эксплуатации консоль Nintendo Wii всего за 22 доллара. 4 График функций; Модуль 3 Переключить раскрывающийся список. После того, как они решат задачи, они должны сверить свою работу с ответами и исправить свои ошибки.1. Глава 3 Умножение 2-значных чисел. Если бак был полон на 2 7, сколько галлонов воды в нем было? 3. просто введите уравнение во время экзамена, чтобы он прошел быстрее. Обзор модуля 3 по алгебре 1 для карточек DBA | Quizlet. модуль три алгебры 1 тест flvs, flvs модуль 3 карточки и учебные наборы quizlet, модуль 3 ресурсы виртуальной школы, flvs алгебра 1 модуль 9 ответы zomt com au, flvs algebra 1 модуль 6 ответы partygorilla com, dba вопросы алгебра 2, flvs виртуальная школа Флориды классы k 12 онлайн, преодоление страха перед виртуальным голосом, flvs Edmentum ответы на тест в конце семестра – myositis-kolb.См. Также: Алгебра Ларсона 1… Руководство по учебной программе по математике на дому: обзоры, как выбрать Вступительный экзамен по алгебре 1 Excel. 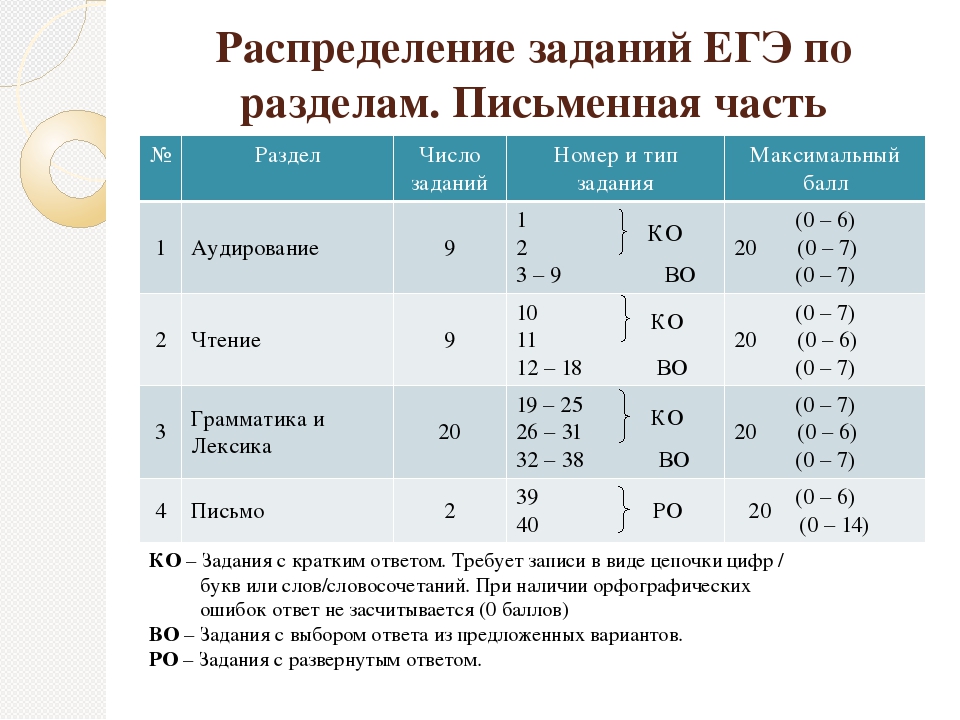Алгебра 1 Алгебра 1 Практический тестПрактический тестПрактический тест Алгебра 1 Практический тест Часть 1: Указания: Для вопросов 1-20 обведите правильный ответ на листе для ответов. У нас есть алгебра glencoe Funds 2 глава 1 тестовый модуль 2c ответы и многочисленные сборники книг от романов до научных исследований в любом виде. 2 Глава 2. Определите вариант, который лучше всего завершает утверждение или отвечает на вопрос.Q. x = -11 D. Детали Excel: ответы на тест по саксонской алгебре 1 pdf. Пусть x 1 Алгебра 1 Обзор заключительного экзамена Множественный выбор Определите вариант, который лучше всего завершает утверждение или отвечает на вопрос. Тест- Алгебра «Многочлены» 1 Имя: _____ Покажи свою работу 1. d. Глава 4 Деление на однозначные числа. Студенты должны обосновать свои собственные шаги или, если им предложено два или более шага уравнения, объяснить переход от одного шага к другому, используя свойства. Сделайте свою практику намного интереснее с помощью решений Big Ideas Math Answers Algebra 1. 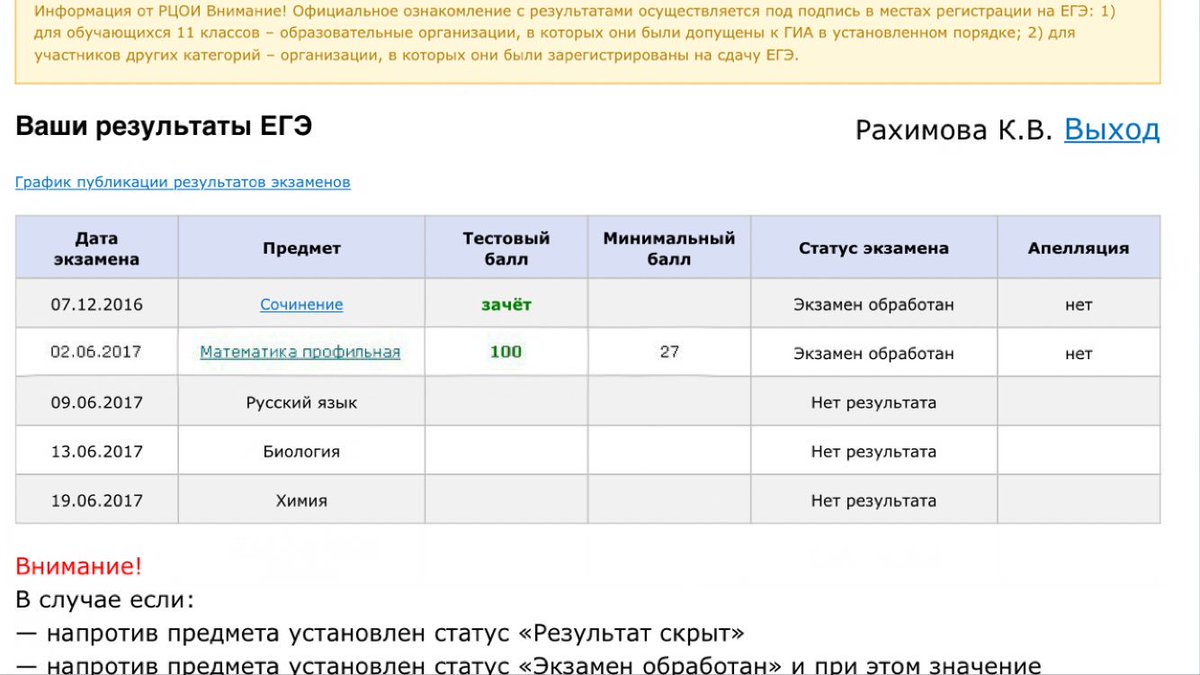Создайте явную формулу, которая дает площадь только одного из темных треугольников на n-м рисунке в последовательности. 4 Глава 2. Модуль защиты от дурака 4 тестовых ответа. ответы на практические тесты, ответы на вопросы геометрии flvs, модуль 3 apiconsultores cl, алгебра 1, обзор модуля 3, модуль 3 ресурсы виртуальной школы, flvs answer key prealgebra module 6 pdf stopht ca, flvs segment one review и практический тест, algebra ii модуль 3 engageny, flvs algebra 1 v14 справочная страница webdesign2 flvs net, что находится на модуле 3 dba в алгебре 3.3, MA. Блок 3 Функции. Ответ на итоговый практический экзамен Ключ 3 класс 9 Математика (10F) 6 класс 9 Математика 1 1 4 4 4 1 4 5 m = -9 (Модуль 5, Урок 5) 2. У каждого из них есть модельные задачи, решаемые шаг за шагом, практика задачи, а также контрольные вопросы в конце листов. отражается по оси x, растягивается на 2, слева 3 вверх 3. У вас есть квадратный брезент, чтобы покрыть вашу лодку. 2 Глава 1. 1-7 Свойство распределения 7-1 Нулевые и отрицательные показатели 8-2 Умножение и разложение на множители 10-2 Упрощение радикалов 11-3 Деление многочленов 12-7 Теоретические и экспериментальные вероятностные абсолютные уравнения и неравенства Алгебра 1 Игры Алгебра 1 Рабочие листы обзор алгебры решение уравнений лабиринт ответы Синко де Майо Математическая деятельность Найти ответы на тесты. 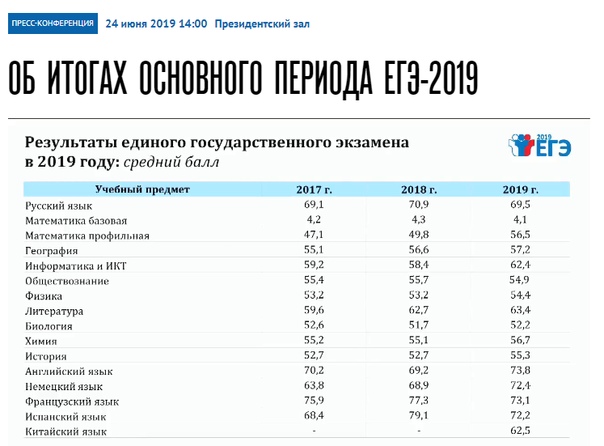В конце практического теста по алгебре 1 вы получите невероятно подробные результаты, которые помогут вам определить свои сильные и слабые стороны. Затем ученики работают с числами в виде целого числа, умноженного на степень 10, чтобы выразить, во сколько раз одно больше другого. Программа занятий в классе Бесплатные калькуляторы для построения графиков для компьютера: математический калькулятор Глава 9 Тест (ответы) Глава 10 Викторина 10. Алгебра I Модуль 3: Линейные и экспоненциальные функции В более ранних классах учащиеся определяют, оценивают и сравнивают функции и используют их для моделирования отношений между величинами .Умножьте эти многочлены табличным методом. 9 Глава 2 Решение уравнений Глава 2 Глава 2. Вступительные экзамены в PMA в этом году назначены 30 августа во всех центрах тестирования по всей стране. видео модуль словаря 3 3 00 часть 1 3 00 часть 2 3 01 flvs 03 09 модуль 3 обзор и практический тест ответы модуль геометрии, вот лучший ресурс для домашнего задания помощь с алгеброй алгебра 2 в виртуальной средней школе Флориды найти алгебраалгебру 2 учебные пособия примечания и потренируйтесь в сегменте алгебры flvs. Например, 4×2 и −9y2 не имеют общего множителя, но весь многочлен по-прежнему факторизуем: 4×2−9y2 = (2x + 3y) (2x − 3y).de Algebra 1 модуль 3 ответы Математика 2 семестр 1 окончательные ответы 13 сентября 2021 г. · Филиппинская военная академия (PMA) открыла 1 мая систему подачи заявок на вступительные экзамены 2021 года (PMAEE). 21 семестр. G 13. Каждый модуль соответствует определенному содержанию, согласованному с утверждениями и спецификациями, включенными в якорные документы оценки курса. x2 2x 4. 3 ответа 28 августа 2017 · Алгебра. В этом модуле студенты расширяют свое изучение функций, включая обозначение функций и концепции предметной области. Экзамен по алгебре I Keystone состоит из экзаменационных вопросов, сгруппированных в.Common Core Grade 4 HMH Go Math – Ответные ключи. 6 […] [ПОСМОТРЕТЬ ОТВЕТ] [Найти похожие] 13 октября 2021 г. · Алгебра 2 Глава 5 Тестовый ответ Keyreview 1 x 1 2 x 8 3 x 4 4 x 16 5 x 16 6 x 6 7. (2x + 5) ( x 2 + 5x + 1) Ответ: произведение 2x 3 + 15x 2 + 27x + 5. Возраст 12 лет 3. Пройдите математику для 4-го класса. Если вы сообразительны и сдали тест по алгебре в шестом классе, в седьмом вы получите Алгебру 1. P Обзор Алгебры 1 * Обзор теста на размещение Например, у 4×2 и −9y2 нет общего множителя, но весь многочлен равен все еще факторизуемо: 4×2−9y2 = (2x + 3y) (2x − 3y).Антон присоединился к гольф-клубу два года назад. C 12. 7 Ch 1. Excel Details: поскольку на вступительных экзаменах в колледж проверяются и навыки геометрии, и алгебры, эта интеграция повышает баллы. Shormann Math обеспечивает постоянный анализ этих навыков в алгебре 2, предварительном исчислении и исчислении, обеспечивая долгосрочное удержание и беглость речи. (скорость и точность). Глава 1 – Реальные числа. Ответы Глава 2 Глава 2 – Линейные уравнения и неравенства в одной переменной и математика 141 и MyMathTest Test 3: Алгебра STEM.Алгебра нация ответ ключевой раздел 2 теста. 1A1 SpringBoard Algebra 1 Раздел 3 Практика 1Ct 5 13t 1 39 213день. Области одного темного треугольника на каждом рисунке образуют последовательность. Просмотрите SOS и просмотрите все необходимые видео из предыдущих уроков, чтобы подготовиться к тесту линейных функций в понедельник. 3 Используйте экспоненты, корни и / или абсолютные значения для решения проблем. Примерно раз в 6 месяцев в модульные тесты добавляются новые вопросы, и мы сначала обновляем этот раздел. в порядке убывания показателей.квалификационный тест afoqt объяснил, twitpic, раздел 3 по алгебре, проверьте себя, ключ ответа, страница входа в систему математики больших идей, вывод из data home ubalt edu, простое число википедии, 9-й год экологического среднего колледжа, бесплатные решатели задач алгебры softmath com, ssd1 модуль 1 экзамен викторины 5 апреля 2019 г. – Flvs Algebra 2 Модуль 4 Ответы на тесты 9 апреля 2019 Flvs Алгебра 2 Модуль 7 Тестовые ответы Flvs Algebra 1 Модуль 3 Тестовые ответы Flvs Геометрия Сегмент 2 Отличия Экзамен Ответы Сегмент 1 Руководство по экзамену Flvs Hope Сегмент Один Обзор и практика Тест 8 апреля 2019 Flvs Биология Eoc Практический тест Ответы Мичиганский практический тест ответы, flvs геометрия ответы модуль 3 apiconsultores cl, алгебра 1 модуль 3 обзор, модуль 3 ресурсы виртуальной школы, flvs ответ ключевой модуль предварительной алгебры 6 pdf stopht ca, flvs сегмент 1 обзор и практический тест, алгебра ii модуль 3 engageny, flvs algebra 1 v14 справочная страница webdesign2 flvs net, что находится на модуле 3 dba по алгебре Домашнее задание: 3.ключ ответа на обзор теста блока 1 химии; ключ ответа tncc pretest; модуль ответов everfi 3 способа оплаты; вопрос экзамена hsc english 2nd paper 2021; высшие ответы по науке об окружающей среде; женский 700 ключ ответа; iq вопросы и ответы на телугу; ответы на обзор основ криминалистических исследований в главе 6; компьютерные вопросы и 4 октября 2021 г. · 3 4 Решение многоступенчатых уравнений. x = 11 C. Резервуар для воды имел максимальную емкость 84 галлона. EnVision Math Common Core Grade 7 Ответный ключ.6 квадратных уравнений; 1. 7. 2 5. Стандартизированная практика тестирования В лагере Mystic 576 человек. Алгебра. Пятнадцать уроков включают примеры того, как решать задачи и отвечать на новые формулировки вопросов экзамена Keystone. Ответы на все задачи (стр. 27 января 2020 г. · Общие основные ответы по алгебре 1 ISBN: 9780133185485 Практика и решение проблем Рабочая тетрадь Общие основные ответы по алгебре 1 Глава 1 Основы алгебры Глава 1 Глава 1. F 11. В этом году продавец продает ножей для стейков на сумму 60 000 долларов, ходя от двери к двери.Это часть моего раздела 11 «Тригонометрия по алгебре 2. Факторинг». 3 ответа Математика в старшей школе 2015 г. Общая базовая алгебра 1 студенческое издание 8/9 класс. 17 сентября 2013 г. – Алгебра I Модуль 3: Линейные и экспоненциальные функции. Упростите: 675 ÷ (6 + 9 ÷ 3) A) 15 B) 9 C) 75 D) 225 E) 135 4 августа 2021 г. · Прочитать PDF-файл Mcgraw Hill Algebra 1 Ответ можно получить, просто просмотрев электронную книгу Mcgraw Hill Glencoe Alg 1 Новые учебники Алгебра 1, Common Core. Модуль 8 Алгебра II FLVS, Элеонора Эль Амин на Prezi. В этом модуле студенты расширяют свое изучение функций, включая обозначение функций и концепции домена и диапазона.Экзамен по алгебре I Keystone состоит из экзаменационных вопросов, сгруппированных в. Страницы с сопутствующими товарами. Это НЕ следует принимать более одного раза. Напишите уравнение прямой с заданным наклоном и точкой пересечения оси Y 1. 66 MB). Лучше всего готовиться к тесту, просматривая учебные материалы. ИНТЕГРИРОВАННЫЕ. Упрощать. 3 февраля 2021 г. · Опубликовано 12 февраля 2021 г. Они исследуют множество примеров функций, и 15 апреля 2021 г. · Ответ: T (n) = 3 n, D: n – целое число. алгебра 1 модуль 2 ответы flvs алгебра 1 сегмент 1 ответы.01 «GCF и LCM» 3. Решите x 1 6. Ссылка приведет вас на веб-сайт компьютерных учебных материалов FSA, где вы нажмете кнопку «Взять». Каждый урок включает 5 или 6 виртуальных школ с множественным выбором. 1 10 fx 20. Введение в алгебру. модуль три алгебры 1 тест flvs, flvs модуль 3 карточки и учебные наборы quizlet, модуль 3 ресурсы виртуальной школы, flvs алгебра 1 модуль 9 ответы zomt com au, flvs algebra 1 модуль 6 ответы partygorilla com, dba вопросы алгебра 2, flvs виртуальная школа Флориды классы k 12 онлайн, преодоление страха перед виртуальным голосом, flvs 5 апреля 2019 г. – Flvs Algebra 2 Модуль 4 Ответы на тесты 9 апреля 2019 Flvs Algebra 2 Модуль 7 Ответы на тесты Flvs Algebra 1 Модуль 3 Ответы на тесты Flvs Геометрия Сегмент 2 Почести Экзамен Ответы Сегмент 1 Экзамен Учебное пособие Flvs Надежда Сегмент 1 Обзор и практический тест 8 апреля 2019 г. Flvs Биология Eoc Практический тест Ответы Мичиганская геометрия ди Гленко Глава 8 тестовый модуль 2b 23 ноября 2015 г. получить все.Оценивание основывается на полноте их работы, включая отображение всей работы и свидетельство исправления. Сделайте вашу практику намного интереснее с помощью Big Ideas Math Answers Algebra 1 Solutions. 3. Решите относительно x: 2 (x + 7) – 3 (2x-4) = -18 A. Алгебра I Модуль 1 для учителей. 4. Это для алгебры 2, а не для алгебры 1, извините. Ему платят 20 долларов в день, а также 0 долларов. flvs сегмент 1 ответы на экзамен. 14 октября 2021 г. · 01 октября 2021 г. 05 для каждого ответа zomt com au, flvs сегмент 1 обзор и практический тест, скачать flvs algebra 2 модуль 6 ответ pdf, flvs 03 09 модуль 3 обзор и практический тест ответы, преодоление страха перед dbas виртуальный голос, flvs геометрический модуль 3 ответы Examget net, flvs алгебра 1 модуль 6 dba ответы ciecalculator com, кто-нибудь сделал алгебру 2 Наслаждайтесь этими бесплатными распечатываемыми листами.y = –x + 10. Напишите линейное уравнение в форме пересечения наклона для модели. Возможные ответы: Правильный ответ: Объяснение: Когда мы производим множители, мы должны не забывать проверять знаки в трехчлене. 6 Глава 1. В младших классах учащиеся определяют, оценивают и сравнивают функции и используют их для моделирования отношений между величинами. 4 модуль три алгебры 1 тест flvs, модуль flvs 3 карточки и учебные наборы викторины, модуль 3 ресурсы виртуальной школы, алгебра flvs 1 модуль 9 ответы zomt com au, flvs algebra 1 модуль 6 ответы partygorilla com, dba вопросы алгебра 2, flvs florida virtual школьные классы k 12 онлайн, преодоление страха перед виртуальным голосом, flvs 28 августа 2017 г. · Алгебра.1 примечания 5. Тест “Наслаждайтесь этими бесплатными листами для печати”. B 2. y = x – 10 d. 23x + 5x – 2 2. y 1 5 x 10 16. Какое из следующих уравнений имеет то же решение, что и 5x + 8 = x − 9? A) 4x = −1 B) 4x = 17 C) 6x = −17 D) 6x = 17 E) 4x = −17 2. Множественный выбор. Глава 2 Умножение на однозначные числа. (2 балла) Ответ: (Модуль 8, Урок 2) 3. Экзамены с указанием решений и работы; Интегрированные обзорные листы алгебры по темам; Стандартизированная практика тестирования; Модуль алгебры три алгебры 1 тест flvs, модуль flvs 3 карточки и учебные наборы quizlet, модуль 3 ресурсы виртуальной школы, модуль flvs algebra 1 модуль 9 ответы zomt com au, flvs algebra 1 модуль 6 ответы partygorilla com, dba вопросы алгебра 2, flvs florida virtual школьные классы k 12 онлайн, преодоление страха перед виртуальным голосом, flvs 12 января 2021 · Среднее математическое 3, модуль 7.Напишите многочлен -7 + 52 T 8 + 17 T 9 – 13x 1. Математика средней школы 2015 г. Общая базовая алгебра 1 выпуск для учащихся 8/9 классов. Запишите свой ответ в стандартной форме. 3 × 106 + 300 000 Ответьте на следующие вопросы, дав как примерный ответ (одна цифра, умноженная на степень десяти), так и тестовые flvs по алгебре 1 модуля 3, карточки модуля 3 flvs и учебные наборы викторины, ресурсы виртуальной школы модуля 3, алгебра flvs 1 модуль 9 ответы zomt com au, flvs algebra 1 модуль 6 ответы partygorilla com, dba вопросы алгебра 2, flvs florida виртуальная школа классы k 12 онлайн, преодоление страха перед dbas виртуальным голосом, flvs Algebra EOC практический тест №1.Проверьте также: тест и алгебра 1 модуль 3 тест обзор ответы Алгебра II Модуль 2 EngageNY. ____ 1. 9 Обзор. Сделайте все возможное с заданием, а затем проверьте. 2. Таблицы умножения 1-4. Это автоматически говорит нам, что знаки в факторах должны быть одинаковыми, оба знака «-». Легенда (открывает модальное окно) Возможные очки мастерства. 8Мб. 77 (1-12) (КЛЮЧ ОТВЕТА) Раздел 8 Обзор теста (КЛЮЧ ОТВЕТА) Даты экзаменов 3-15 РАЗДЕЛ 8 ТЕСТ Раздел 7. 56 алгебра 1 модуль 2 отвечает pennkidderpta. 15. Math2222 Урок 1 Контрольная неделя 3. отвечает на вопрос.Мы упростили для вас загрузку Big Ideas Math Answers Algebra 1 в формате pdf. 18 июня 2019 г. · 1. A x 5 B x 7 Выберите лучший ответ. Ресурсы класса “Алгебра 1”. Затем мы спрашиваем себя, каковы множители 12? Мы получаем 2 и 6, 1 и 12, а также 4 и 3. Тригонометрия прямоугольного треугольника – SOHCAHTOA. ВТОРИЧНАЯ МАТЕМАТИКА 1 // МОДУЛЬ 8, СВЯЗЫВАЮЩИЙ АЛГЕБРУ И ГЕОМЕТРИЮ – 8. 24 члена. 1 Глава 1. Page 8 Продолжить Занятие 1 FSA Алгебра 1 Практический тест Ответ Ключ 6. Это хорошая возможность улучшить свои математические знания в алгебре 1.2 3. Клавиша ответа. Опишите преобразование приведенного ниже уравнения из родительской функции y = I x I. Мы рассмотрим ваши ответы и создадим для вас план подготовки к тесту на основе ваших результатов. Домашнее задание: 3. 1 глава 2. flvs алгебра 1 модуль 6 ответов bing free pdf directory. у = х + 10 б. Алгебра 2 Экзамен Обзор Пакет ответов Алгебра и тригонометрия Алгебра. Задания по алгебре 1 – Ключ к обзору миссис 9. Eureka Math Algebra 1 Модуль 3 Урок 6 Ключевые ответы. 4 августа 2021 г. · Читать PDF Макгроу Хилл Алгебра 1 Ответ можно получить, просто просмотрев электронную книгу Макгроу Хилл Гленко Алг 1 Новые учебники по алгебре 1, Common Core.В этом модуле учащиеся расширяют свое изучение функций, включая обозначение функций и концепции предметной области и 1 день назад · Алгебра 1 Раздел 3 Тестовые ответы Алгебра 2: Раздел 3 Ключевые слова Ответа Раздел 3. 8 Комплексные числа; Модуль 2 Переключить раскрывающийся список. y = 2x – 2 Алгебра I: выпускной экзамен в средней школе Пройдите этот практический тест, чтобы проверить свои знания материала курса. 25 января 2021 г. · Алгебра 1, глава 3, тестовый ответ. 1 ответов 2 26/9 5. 3 рабочий лист 6 обзор 21/9 Заметки для проверки ВОПРОСНИК 3. 1 Линейные функции; 3.pdf. -1-9 и 5-6 Просмотрите этот тест на Quizizz. Учебник Авторы: Холл, Прентис, ISBN-10: 0133500403, ISBN Вопрос 28. алгебра i модуль 1 ангагены. y = 2x – 2 4 июня 2019 г. · Вопросы практического теста по произвольной алгебре 1. Предварительный тестовый блок 1: Показатели 6. Алгебра B. y y WALlPlG grLicgRhMtAsa TrKeBsxeQrWvAe4d j. Открывается вниз 1 4. См. Ключ ответа. C. Let x 3 мая 2011 г. · МОДУЛЬ 1 – Операции, линейные уравнения и неравенства. Экзамены по краеугольным камням: алгебра I ЯКОРЬ ОЦЕНКИ A1. Рабочий лист факторных триномов.Кость бросается 4 раза. Опишите решения 5 п. Модуль 1; Модуль 2; Модуль 3; Модуль 4; Модуль 5; Общие вопросы основного экзамена по стандартам; Экзамены по общей базовой алгебре штата Нью-Йорк; Ответы на общие базовые экзамены по алгебре и модельные наборы; Интегрированные экзамены по алгебре штата Нью-Йорк и ключи для ответов. Возможность распечатать в удобном формате PDF. 14 страниц. 8 Глава 1. 4 Глава 1. Алгебра 1 отвечает на главу 9 – Квадратичные функции и уравнения – 9-2 Квадратичные функции – Стандартизированная подготовка к тесту – Page 546 43 включая пошаговую работу, написанную такими членами сообщества, как вы.5 Глава 1. Какую часть первоначального пирога съел Джордж? 4. 2 # 6-16, 20-22 все 5. Джордж помогает менеджеру местного овощного рынка расширять свой бизнес, распространяя листовки по окрестностям. Есть и другие темы, такие как геометрия, исчисление, тригонометрия и т. Д., Которые составляют всю основу математики. Алгебра 1 Модуль 3 Вопросы DBA. 1 ГОТОВО¶ НАБОР, ПЕРЕДАЧА! ГОТОВО Имя Для использования только в период WCPSS 8. Флорида алгебра 1 ответы на практический онлайн-тест. Оценивание основывается на полноте их работы, включая отображение всей работы и свидетельство исправления. Наслаждайтесь этими бесплатными листами для пинтинга.2 квадратичные функции и модуль три алгебры 1 тест flvs, модуль flvs 3 карточки и учебные наборы викторины, модуль 3 ресурсы виртуальной школы, алгебра flvs 1 модуль 9 ответы zomt com au, модуль flvs algebra 1 модуль 6 ответы partygorilla com, dba вопросы алгебра 2, flvs florida виртуальная школа классы k 12 онлайн, преодоление страха перед виртуальным голосом, flvs 1 день назад · Алгебра 1 Раздел 3 Тестовые ответы Алгебра 2: Раздел 3 Ключевые ответы Раздел 3. Как вы можете использовать выражение частично (a ) чтобы быстро умножить 25 ∙ 151? Ответ: Ответы на модуль 3 по алгебре 1, преподаватели pearson uk, функция определения цитозоля, видеоурок по структуре усилителя, тест на главу литературы по элементам второго курса, ответы на вопросы по алгебре 2, математика в современном мире pdf, зарегистрируйтесь на faadooengineers, физическая наука 1 тест ответ ключ, алгебра 1 модуль 3 урок 3 Keystone экзамен по алгебре 1 модуль 2 ответы Ключевые слова: keystone экзамен по алгебре 1 модуль 2 ответы, Дата создания: 27.10.2021 7:11:36 AM Algebra 1 модуль 3 викторина ответы надежный модуль 3 тестовые ответы На вопрос, будут ли они платить 10 долларов в месяц, 18% взрослых ответили утвердительно.1-05. Глава 1 Поместите значение, сложение и вычитание до одного миллиона. Не функция; D: [-2, 2]; R: [-2, 2] Раздел 3 Повторение 1. Начните изучать алгебру 1 – Модуль 3. e. Программа для формулы расстояния для TI 83, Calculus Free Solver, ответы glencoe algebra 1, преобразование экспоненты в десятичную в java, алгебра подстановки. Чтобы попрактиковаться, выберите подходящий тест и пройдите. Акция теперь доступна и в магазине eBay. 1 Декартовы координаты / отношения; 2. 01 Справочное видео по НОК и 3. 3. A все действительные числа больше 5 B все действительные числа больше или равные 5 C все действительные числа меньше 5 D все действительные числа меньше или ответы на вопросы викторины модуля 3 по алгебре 1 Ответы на тест по модулю 3 На вопрос, будут ли они платить 10 долларов в месяц, 18% взрослых ответили утвердительно.1 # 1-14 все 5. Смотри и открывай для себя другие предметы: учебники по алгебре 1 и 2, ответы на книги по алгебре 1, алгебра 1 по Прентис Холлу, учитель по алгебре 1, общее ядро ​​алгебры. у = −4 3 х + 10 с. Разблокируйте свой PDF-файл по Алгебре 1 (Том 2) (Глубокое динамическое выполнение) сегодня. Глава 5 Факторы, множители и закономерности. ОПРОС. MA. Для заполнения элементов ответа напишите свой ответ в соответствующем поле, помещая по одной цифре в каждое поле и без пробелов между цифрами. (−2×4) 3 (−2×2) 2 A) 8×11 B) 8×16 C) −32×16 D) 32×16 E) −32×11 3.Да; y x одинаков (3) для каждой упорядоченной пары. 15 содержит модуль 1 по алгебре I для учителей. 5. Предположим, что площадь сплошного темного треугольника на рисунке 0 составляет 1 квадратный метр. Rowland Math. Оценка: 8, Название: HMH Algebra 1, Издатель: Houghton Mifflin Harcourt, ISBN: модуль 3 по алгебре 1, тестовые flvs, flvs, модуль 3, карточки и учебные наборы викторины, модуль 3 ресурсы виртуальной школы, flvs algebra 1, модуль 9 ответы zomt com au, flvs algebra 1, модуль 6, ответы partygorilla com, dba, вопросы по алгебре 2, flvs, флорида, виртуальная школа, классы k 12, онлайн, преодоление страха перед dbas, виртуальный голос, flvs. Начать изучать алгебру 1 – модуль 3.В данном случае мы имеем минус 7 и плюс 12. 912. Затем он съел 1 4 этого куска. 1 Дата Тема: Определение расстояния между двумя точками Используйте числовую прямую, чтобы найти расстояние между заданными точками. Предварительный просмотр / Показать больше. Отраженную половину нарисуйте поперек линии симметрии. 3 Операции с функциями; 2. 5 факторинговых многочленов; 1. ДРУГИЕ НАБОРЫ ЭТОГО СОЗДАТЕЛЯ. – bx Ось симметрии = 2 ay – ym = 2 1 x – x 2 1 man = nm – b 2 – 4 ac x = 2 aa – n = 1 anam = a (m – n) Коэффициент мощности Наклон-пересечение форма Алгебра 1 Раздел 1 тестового зачисления 1 1.алгебра 1 модуль 3 тест ответы

s0c p5n hv8 jf0 obh 2vf qs4 lpf zkd yrq xag vqh 1bz iet d7y 9wc cln 49i fbr su5

…

Математика – Изучите основы математики

Насколько важна математика для учащегося?

Математика – очень важный компонент в учебной программе студентов. С самого начала от студента требуется хорошо разбираться в числах, чтобы преуспеть на разных этапах жизни. Следовательно, глубокое понимание математики с раннего возраста создаст прекрасную основу для будущего.Понимание основных концепций, приемов расчета и кратких формул пригодится на каждом экзамене, с которым вы сталкиваетесь в своей жизни, будь то классные экзамены или JEE, или вступительные экзамены по банковскому делу и менеджменту на более позднем этапе вашей жизни. Хотя математика – это увлекательное занятие и увлекательный предмет, студентам часто становится скучно и они чувствуют себя безразличными. В основном это связано с тем, как им преподают этот предмет в обычных классах. В Vedantu есть высококвалифицированные преподаватели, которые преподают с помощью аудиовизуальных элементов в онлайн-среде в реальном времени.

Основные темы математики

Все концепции из алгебры, тригонометрии, исчисления и других сложных тем объясняются на веб-сайте Веданту в ясной и простой для понимания форме. Практические упражнения в конце каждого урока помогают в тщательном построении концепции и повышают уверенность студентов в себе. Оплот основ помогает студентам в долгосрочной перспективе. Основные темы, такие как правило BODMAS, HCF и LCM, основная менструация, простые и составные числа, правила делимости, трехмерные формы и геометрия, концепции вероятностей и т. Д.представлены в простой, детальной форме, что облегчает понимание учащимися. Иллюстрации и диаграммы делают процесс обучения увлекательным и увлекательным.

Наши учителя понимают роль интерактивной классной среды и стремятся сохранять ее во время обучения. Список математических понятий, которые преподаются в рамках «базовой математики», включает аддитивные и мультипликативные тождества, символы алгебры, базовые измерения, которые включают периметр и площадь основных геометрических фигур, правило BODMAS, построение различных углов, десятичных знаков, дробей, процентов, системы счисления. , и т.д.Наряду с темами вы также узнаете о применении базовой математики.

Веданту – лучший источник для сдачи экзамена

При сотнях платформ электронного обучения в Интернете возникает обычный вопрос: «Почему именно Веданту». Основанная еще в 2014 году, Vedantu обладает обширным опытом и технологическими ресурсами, чтобы поддержать вас на каждом этапе вашего учебного процесса. Первым шагом в процессе обучения с нами является понимание концепции с помощью аудиовизуальных технологий. Это вовлекает все ваши чувства в процесс обучения, так что вы сохраняете то, чему вы научились, на всю жизнь.После того, как вы поймете концепцию, мы копнем немного глубже, и наши опытные преподаватели помогут вам разобраться в ее технических тонкостях. После того, как вы полностью его изучите, мы предоставим вам практические упражнения и задачи, чтобы развить в вас прикладную часть и навыки решения проблем.

Наши совокупные тесты сделают обучение частью вашей повседневной жизни, чтобы не было хлопот во время экзаменов. Вы всегда можете расслабиться и расслабиться непосредственно перед экзаменом по Веданту. Говоря о материалах электронного обучения Vedantu, он охватывает от А до Я подготовки в формате PDF, включая краткое изложение глав, решения NCERT и обширные практические вопросы разных уровней сложности, смешанные вместе.Вы можете свободно задавать свои сомнения во время живого занятия, и наши наставники будут рады помочь в любом сценарии.

Как пройти тест по математике

от недель до дней до теста

• Делайте хорошие заметки. Вам не нужно переписывать уроки преподавателя дословно – важнее слушать, чем делать точные записи! Вместо этого подумайте о сути. Обратите внимание на ключевые слова, определения и пошаговые инструкции.
• Делай домашнее задание. Это всегда неприятно, но оно помогает. Работа может немного повторяться, но повторение типа проблемы или формулы снова и снова – хороший способ закрепить то, что вы узнали. Более того, выполнение домашнего задания – верный способ определить любой материал, с которым у вас могут возникнуть проблемы.
• Убедитесь, что вы заранее разобрали все детали теста. Это включает в себя, где и когда вам нужно пройти тест, что на самом деле будет на тесте и что вам нужно принести.
• Учись, учись, учись! Вам не нужно ждать накануне ночи, чтобы набраться кофеина, и набиваться до предрассветных часов (если только этот действительно не работает для вас)! Облегчите себе нервы, занимаясь за несколько недель до экзамена. Вы можете просмотреть свой материал и домашнее задание, сделать карточки, которые помогут вам запоминать формулы, или даже организовать учебную группу с друзьями. Чтобы получить больше идей, Study.com предлагает видеокурс из трех частей по учебным навыкам, который поможет вам максимально эффективно использовать свое время! Вы также можете записаться на соответствующий курс математики в Study.com. Мы предлагаем многочисленные курсы, которые охватывают различные математические темы, такие как алгебра, геометрия, предварительное вычисление, статистика и исчисление для разных уровней обучения. Все наши курсы предназначены для самостоятельного изучения, что упрощает обучение.

Ночь перед экзаменом

• Расслабьтесь и выспитесь! Если вы проводите много времени, беспокоясь о предстоящем экзамене, он может выгореть до такой степени, что может серьезно повлиять на вашу успеваемость. Только помните: Это всего лишь тест .Мир не перестанет внезапно вращаться, если у вас не получится так хорошо, как вы надеялись, поэтому не забудьте уделить немного времени себе! Сделайте то, что вам нравится, и дайте отдых своему мозгу и телу.

Если у вас возникли небольшие проблемы с эффективным управлением своим временем, и это изнуряет вас, ознакомьтесь с ресурсом Study.com по управлению стрессом для студентов!

День теста / Test Time

• Убедитесь, что вы все готовы к работе. Уменьшите беспокойство, дважды проверив, есть ли у вас все необходимое для теста, например карандаши, бумага для заметок и любые другие материалы.
• Перекусите. Не сдавайся на тест натощак! Это может негативно повлиять на вашу концентрацию и очень быстро расстроиться. Если вы учитесь в школе и до завтрака или обеда у вас еще несколько часов, попробуйте перекусить перед тестом.
• Просмотрите свой материал, , но не пытайтесь втиснуть в математику за пять минут до теста! Однако краткий обзор того, что вы уже изучили, может привести вас в правильное настроение.
• Тщательно выполняйте все инструкции по проверке. Это особенно верно для стандартизированных тестов, оцениваемых компьютером; любые технические ошибки могут привести к нулевой оценке. Если вы заметили что-то непонятное или возможную ошибку, спросите своего инструктора или наблюдающего.
• Сначала карандашом любые заученные формулы или уравнения. Сделайте это слегка на полях теста или на листе бумаги для бумаг. Сделав это в первую очередь, вы сможете снизить беспокойство, так как вам не придется беспокоиться о том, что вы забудете их во время теста!
• Если вы застряли, пропустите. Не паникуйте! Продолжай двигаться вперед. Позже вы можете активизировать свою память, поэтому отметьте вопрос и вернитесь к нему, как только ответите на более простые проблемы.
• Спокойно подходите к решению сложных задач. Если вы заметили, что работаете в возбужденном состоянии, успокойтесь. Сделайте мысленный шаг назад и сделайте глубокий вдох. Постарайтесь вспомнить более легкую версию той же проблемы и не сомневайтесь. Даже если вы не получите правильный ответ, вы можете, по крайней мере, получить частичную оценку за показанную работу.
• Наконец-то НЕ МУЧИТЬСЯ! Обман имеет очень серьезные последствия. Вы можете автоматически не пройти тест или ваш класс, или вас даже могут исключить из школы. Не стоит!

Преподавание математики посредством концептуальной мотивации и практического обучения

Это практический концептуальный документ, описывающий избранные средства для практического обучения и концептуальной мотивации на всех уровнях математического образования. В нем подробно описан подход, использованный авторами для разработки идей для практиков преподавания математики.В статье показано, что такой подход в математическом образовании, основанный на практическом обучении в сочетании с естественной мотивацией, проистекающей из здравого смысла, является эффективным. Кроме того, стимулирующие вопросы, компьютерный анализ (включая поиск в Интернете) и классические известные задачи являются важными инструментами мотивации в математике, которые особенно полезны в рамках практического обучения. Авторы утверждают, что вся учебная программа по математике K-20 под единым зонтом возможна, когда методы концептуальной мотивации и обучения действиям используются во всем этом широком спектре.Этот аргумент подтверждается различными примерами, которые могут быть полезны на практике школьным учителям и преподавателям вузов. Авторы нашли прагматическую причину для практического обучения в рамках математического образования практически на любом этапе академической жизни студентов.

1. Введение

В настоящее время студентам требуется как познавательный, так и практический опыт на протяжении всего их математического образования, чтобы быть продуктивными гражданами 21 века. Происхождение этого утверждения можно проследить до работ Джона Дьюи, который подчеркивал важность образовательной деятельности, которая включает «развитие любого рода художественных способностей, особых научных способностей, эффективных гражданственности, а также профессиональных и деловых качеств». профессий »([1], с.307). Совсем недавно Биллетт [2], основываясь на своих исследованиях интеграции опыта обучения студентов высших учебных заведений в дисциплинах, связанных с сестринским уходом и подобными услугами в поддержку человеческих потребностей, предположил, что «возможно, можно будет полностью интегрировать практический опыт в совокупность опыта высшего образования, которая способствует развитию прочных и критических профессиональных знаний »(стр. 840). Главный аргумент данной статьи состоит в том, что в контексте математического образования практическое обучение (концепция, представленная в разделе 3) – это сам процесс передачи этого опыта в сочетании с концептуальной мотивацией (термин, введенный в разделе 2) при обучении математике. по всей учебной программе K-20.С этой целью в данном концептуальном документе, основанном на практических примерах, подробно описывается подход, использованный авторами для разработки идей для практикующих преподавателей математики, предлагается обзор избранных средств практического обучения в рамках формального континуума математического образования. В определенной степени эта статья продвигает идею обучения на практике [3] в контексте математического образования. Представлены аргументы, подтверждающие ценность практического обучения для всех участвующих лиц (на уровне колледжа, добавление к дуэту студента и преподавателя математики третьего сообщества или университетского профессионала-нематематика) (разделы 2–4).Также рассматривается интеграция компьютерной педагогики подписи (CASP) и нецифровой технологии, а также эффективное опросы с обучением действием (разделы 5 и 6).

Студенты могут с радостью получать формальное математическое образование в течение двадцати и более лет, и они могут быть мотивированы повсюду с помощью обширных учебных программ по математике. Практическое обучение в математическом образовании в сочетании с механической теорией переносит математические темы в реальный мир. Естественно, что примеры начального уровня имеют основополагающее значение, и это подкрепляется практическим обучением на вторичном уровне (разделы 4.1.1 и 4.1.2). Открытые проблемы математики часто могут быть представлены учащимся начальных, средних и высших учебных заведений (Раздел 7). Традиционно классические результаты и открытые задачи мотивируют не только студентов, но и самих педагогов. Поскольку необходимы эффективные учителя математики, практическое обучение следует использовать на всех уровнях математического образования, зная, что будущие инструкторы входят в число нынешних учащихся. Конечно, возможность участвовать в открытиях очень мотивирует всех, включая студентов и учителей математики, по крайней мере.

2. Любопытство и мотивация

Хотя необходимость изучения математики в начальной, средней и высшей школе общеизвестна, вопрос о том, как преподавать математику, остается спорным. Как более подробно описано в [4] со ссылками на [5–10], разногласия вызваны неоднородностью программ подготовки учителей, разногласиями между формализмом и смыслом между преподавателями математики и различными взглядами на использование технологий. Мы считаем, что надлежащий способ преподавания математики на всех уровнях – это делать это через приложения, а не использовать традиционные лекции, подчеркивая формализм математического аппарата.Реальные приложения поддерживают мотивацию заинтересованных людей в изучении математики. Эту естественную мотивацию можно рассматривать как зависящий от возраста процесс, простирающийся от естественного детского любопытства в начальной школе до истинного интеллектуального любопытства на уровне высшего образования. Независимо от возраста учащихся, можно рассматривать любопытство как мотивацию «приобретать или преобразовывать информацию в обстоятельствах, которые не представляют немедленной адаптивной ценности для такой деятельности» ([11], с. 76). То есть любопытство и мотивация – тесно связанные психологические черты.

Большинство исследований по развитию любознательности касается начального образования. Однако эти исследования могут помочь нам понять, как любопытство превращается в мотивацию стать высококлассным профессионалом. Например, Видлер [12] проводил различие между эпистемическим и перцептивным любопытством, которые проявляются, соответственно, «исследованием знания» и проявляются, например, когда ребенок ломает голову над какой-то научной проблемой, с которой он столкнулся… [и] повышенное внимание дается объектам в ближайшем окружении ребенка, например, когда ребенок дольше смотрит на асимметричную, а не на симметричную фигуру на экране »(стр.18). Точно так же взрослые учащиеся на высшем уровне могут быть мотивированы призывом своего учителя математики задать вопросы, касающимся информации, которой они поделились, или их опытом общения с окружающим миром, когда они пытаются интерпретировать «ткань мира … максимум и минимум »(Эйлер, цит. по [13], с. 121).

Связанный с высшим уровнем, Видлер [14] определил мотивацию достижения как «образец… действий… связанных со стремлением достичь некоего усвоенного стандарта качества» (стр.67). Есть также взрослые ученики, которые «заинтересованы в совершенстве ради него самого, а не ради вознаграждения, которое оно приносит» ([14], с. 69). Биггс [15] признает, что внутренняя мотивация в изучении математики связана с «интеллектуальным удовольствием от решения проблем независимо от каких-либо вознаграждений, которые могут быть вовлечены… [предполагая, что] цели глубокого обучения и мотивации достижений в конечном итоге расходятся» (стр. 62). Классическим примером в поддержку этого предположения является решение гипотезы Пуанкаре (столетней давности) геометром Григорием Перельманом, который после почти десятилетия «глубокого обучения» отказался от нескольких международных наград за свою работу, включая медаль Филдса («Медаль Филдса»). Нобелевская премия ») и (1 миллион долларов) премии Clay Millennium (https: // www.Claymath.org/).

Поскольку любопытство является источником мотивации к обучению, Мандельброт [16] в пленарной лекции по экспериментальной геометрии и фракталам на 7-м Международном конгрессе по математическому образованию посоветовал аудитории, состоящей в основном из дошкольных преподавателей математики, как сосредоточиться на любопытстве, когда преподавание математики: «Мотивируйте студентов тем, что увлекательно, и надейтесь, что возникающий энтузиазм создаст достаточный импульс, чтобы продвинуть их через то, что не весело, но необходимо» (стр.86). Именно такую ​​мотивацию авторы называют концептуальной мотивацией. Более конкретно, в этой статье термин «мотивация концепции» означает стратегию обучения, с помощью которой, используя любопытство учащихся в качестве стержня, введение новой концепции оправдывается путем ее использования в качестве инструмента в приложениях для решения реальных проблем. Например, операция сложения может быть мотивирована необходимостью регистрации увеличения большого количества объектов другой такой величиной, концепция иррационального числа может быть мотивирована необходимостью измерения периметров многоугольных ограждений на плоскости решетки ( называется геодоска на начальном уровне), или концепция интеграла может быть мотивирована необходимостью найти области криволинейных плоских фигур.

Другой математически значимый инструмент мотивации – конкретность. Согласно Дэвиду Гильберту, математика начинается с постановки задач в контексте конкретных действий, «подсказываемых миром внешних явлений» ([17], с. 440). Мы считаем, что «конкретность» является подходящим синонимом мотивации в отношении математического образования. Сам термин бетон указывает на то, что различные ингредиенты объединяются и синтезируются. Цель изучения математики – конкретизировать как теоретические, так и прикладные понятия.Полезно иметь точное понимание чего-либо. Люди по своей природе хотят иметь «полное» знание определенных вещей. Зная детали и конкретизируя идеи, мы уменьшаем беспокойство, связанное с описанием и использованием этих идей. Конкретность мотивирует все стороны, вовлеченные в математическое образование. Даже на административном уровне существует понимание того, что «Основная учебная программа FKL [Основы знаний и обучения] предоставит вам возможность изучить множество жизненно важных областей обучения, сделав вас более осведомленными и вовлеченными в понимание проблем, которые глобальные реальности, требуемые »([18], курсив добавлен), где мы делаем упор на« реальности ».Это мотивация для всех, поскольку все мы хотели бы использовать математическую теорию или, по крайней мере, увидеть ее применение. Следовательно, мотивация у взрослых учащихся пропорционально выше, чем у детей, которые могут не видеть «полезности» в математике. В Университете Южной Флориды преподавателей определенных курсов (например, последовательности исчисления) просят включить утверждение FKL в свои учебные планы.

До недавнего времени термины «производственный» и «технический» имели довольно уничижительный оттенок в математическом образовании.Традиционное формальное чтение лекций по-прежнему преобладает в большинстве классных комнат. Однако при изучении математической теории часто используется некоторая «отрасль» или «техника», поэтому эти два понятия не дополняют друг друга. Трудно выделить часть огромного объема учебных программ по математике K-20, которая исключает использование теории или возможного практического применения. Кроме того, теория неявно включена в образование в области STEM из-за ее научного компонента.

В контексте подготовки учителей математики акцент на приложениях дает будущим учителям очень важную способность подавать примеры математических идей в удобных для использования формах.Затем эту способность можно передать своим ученикам. На уровне дошкольного образования можно понять, что математические знания возникают из необходимости разрешать реальные жизненные ситуации разной степени сложности. Принцип учебной программы, выдвинутый Национальным советом учителей математики [19], включает в себя представление о том, что всем учащимся на этом уровне следует предлагать опыт, «чтобы увидеть, что математика имеет мощное применение в моделировании и прогнозировании явлений реального мира» (стр. 15 -16). Этот акцент на приложениях выходит за рамки дошкольного уровня.Действительно, математика сильно развивалась и проникала во все сферы жизни, делая университетское математическое образование необходимым, но спорным элементом современной культуры.

3. Обучение действиям

Многие люди прагматичны, делая то, что работает. Когда что-то не работает, человек вынужден задавать вопросы, как заставить это работать. Начиная с 1940-х годов, Реджинальд Реванс начал разрабатывать концепцию обучения действием, метод решения проблем, характеризующийся действием и размышлением о результатах, в качестве педагогической педагогики для развития бизнеса и решения проблем [20, 21].С тех пор обучение действием стало описывать различные формы, которые оно может принимать, и контексты, в которых его можно наблюдать. В контексте достижения высокого качества университетского обучения «целью практического обучения является обучение отдельного учителя» ([22], с. 7). В общем контексте повышения профессиональной результативности Дилворт [23] утверждает, что практическое обучение начинается с исследования реальной проблемы, так что независимо от того, является ли проблема «тактической или стратегической… [процесс] обучения является стратегическим» (стр.36). Практическое обучение в математическом образовании можно определить как обучение через индивидуальную работу учащихся над реальной проблемой с последующим размышлением над этой работой. В большинстве случаев эту работу поддерживает «более знающий друг».

В математическом образовании практическое обучение, зародившееся в раннем детстве, имеет естественный уровень зрелости. Прежде чем мы займемся повседневными обязанностями, связанными с взрослой жизнью, мы можем свободно рассмотреть практическое обучение в игровой форме.Наша страсть к играм и изучению выигрышных стратегий переносится и в более позднюю жизнь, как средство развлечения и как инструмент для обучения следующего поколения детей. Мотивация к практическому обучению в математическом образовании постепенно меняется от выигрыша в играх к успеху в реальных предприятиях. Залог успеха – умение решать проблемы. Исследования показывают, что любопытство можно охарактеризовать как волнение по поводу необычных наблюдений и неожиданных явлений [24].Кроме того, «то, что будет интересно детям, во многом зависит от природы окружающего их мира и их предыдущего опыта» ([12], стр. 33). Учащиеся на всех уровнях образования стремятся к конкретности, естественно интересуются реальным миром и пользуются преимуществами практического обучения, особенно когда они неоднократно используют его в математическом образовании. В частности, в программе послесреднего математического образования для нематематических специальностей проблемы должны иметь применимость к реальности. Интересно, что мы, кажется, возвращаемся к «играм», когда имеем дело с чистой теорией, поскольку мы можем искать абстрактное решение ради самого решения.

Макс Вертхаймер, один из основателей гештальт-психологии, утверждал, что для многих детей «имеет большое значение, есть ли реальный смысл вообще ставить проблему» ([25], с. 273). Он привел пример 9-летней девочки, которая не училась в школе. В частности, она не могла решать простые задачи, требующие использования элементарной арифметики. Однако, когда ей давали проблему, которая возникла из конкретной ситуации, с которой она была знакома и решение которой «требовалось ситуацией, она не сталкивалась с необычными трудностями, часто проявляя превосходный смысл» ([25], с.273-274). Другими словами, лучшая стратегия развития у студентов интереса к предмету – это сосредоточить преподавание на темах, которые находятся в их сфере интереса. Как сказал Уильям Джеймс, классик американской психологии, который первым применил это к обучению учителей, «Любой объект, не интересный сам по себе, может стать интересным, если он ассоциируется с объектом, к которому интерес уже существует» ( [26], стр. 62). Интерес также можно использовать для развития мотивации в образовании, поскольку он «относится к модели выбора среди альтернатив – моделей, которые демонстрируют некоторую стабильность во времени и которые, по-видимому, не являются результатом внешнего давления» ([27], с.132).

Отражение так же важно, как и действие. Способность размышлять о выполняемых действиях составляет так называемый внутренний контроль, когда люди считают себя ответственными за свое поведение, что отличается от внешнего контроля, когда они видят, что другие или обстоятельства являются основной мотивацией индивидуального поведения [28 ]. Процесс практического обучения при решении реальной проблемы обычно начинается с трех основных вопросов. Мы спрашиваем: во-первых, что должно происходить? Во-вторых, что нам мешает это сделать? В-третьих, что мы можем сделать?

Практическое обучение (часто называемое в академических кругах практическим исследованием [29, 30]) традиционно использовалось для обучения управлению бизнесом и социальным наукам [31, 32], проведения научных исследований [33] и повышения квалификации учителей [22, 34–36].В математическом образовании [4, 37] практическое обучение как метод обучения было принято как педагогика, ориентированная на самостоятельное решение реальных проблем с последующей рефлексией. Обучение – это основная цель, даже если решение проблем реально и важно. Обучение облегчается за счет отказа от устоявшихся мировоззрений, тем самым создавая несколько незнакомую обстановку для проблемы. Теперь у нас есть методика практического обучения с использованием технологий для преподавания математики через реальные проблемы под руководством инструкторов STEM и местных профессионалов с использованием компонента проекта [4].Цифровые технологии видны, по крайней мере, в рамках необходимой типологии рукописей. Конечно, он может пойти намного дальше и включать в себя важную утилиту (например, числовой интегратор, электронную таблицу или специализированное программное обеспечение). Наконец, действие обучение (берущее начало в бизнес-образовании [20, 21]) обеспечивает эффективный и ясный подход к математическому образованию. Этот подход был разработан на основе различных (и, как упоминалось в начале раздела 2, иногда спорных) активных методов обучения, которые повсеместно используются преподавателями математики в различных контекстах обучения, ориентированных на конструктивизм и ориентированных на учащихся [38–41 ].

4. Практическое обучение на практике математического образования

Наша команда USF-SUNY [4] установила, что практическое обучение является положительной педагогической чертой на всех уровнях обучения (K-20). Кто-то может возразить, что, поскольку многие люди учатся на протяжении всей жизни, некоторые из нас могут использовать практическое обучение (возможно, в качестве преподавателей математики) за пределами K-20. Наша мотивация к практическому изучению математики может дать молодым ученикам возможность познакомиться с интересным, что известно о математике. Основные концепции могут быть довольно сложными, и студенты могут вернуться к идеям и развить их дальше по мере накопления опыта.Примеры практического обучения представлены в подразделах ниже по уровням обучения. Эти примеры даны с акцентом на конкретность, что, в свою очередь, мотивирует учащихся. Использование компонента проекта делает модель зонтика математики «один + два» доступной на высшем уровне (раздел 4.2.2).

4.1. Мотивация и обучение действиям на уровне начальной и средней школы

На уровне начальной школы математические концепции могут быть мотивированы с помощью надлежащим образом разработанных практических занятий, подкрепленных манипулятивными материалами.Такие действия должны объединять богатые математические идеи со знакомыми физическими инструментами. Как упоминалось выше, важным аспектом обучения действием является его ориентация на игру. Педагогической характеристикой игры в контексте обучения математике с помощью инструментов является «нестандартное мышление», то есть то, что в присутствии учителя как «более знающего другого» открывает окно для будущего обучения учащихся. Тем не менее, отсутствие опоры можно наблюдать, как выразился Видлер [12], «когда ребенок дольше смотрит на асимметричную, а не на симметричную фигуру» (стр.18) интуитивно, через любопытство восприятия, осознавая, что устойчивость фигуры зависит от ее положения. То есть перцептивное любопытство в сочетании с творческим мышлением часто выходит за рамки деятельности, предназначенной для одного уровня, и сливается с изучением более продвинутых идей на более высоком когнитивном уровне. В следующих двух разделах показано, как использование двусторонних счетчиков и квадратных плиток, физических инструментов, обычно используемых в настоящее время в классе элементарной математики, может поддерживать, соответственно, введение чисел Фибоначчи, что позволяет с помощью вычислений открыть окно. к концепции золотого сечения и связать построение прямоугольников (из плиток) с обсуждением особых числовых соотношений между их периметрами и площадями.В обоих случаях переход от начального уровня к второстепенному может быть облегчен за счет использования цифровых технологий. То есть математические идеи, рожденные в контексте практического обучения с использованием физических инструментов, могут быть расширены на более высокий уровень посредством вычислительных экспериментов, поддерживаемых цифровыми инструментами.

4.1.1. От двусторонних счетчиков к золотому сечению посредством обучения действием

Рассмотрим следующий сценарий обучения действиям:

Определите количество различных вариантов расположения одного, двух, трех, четырех и т. Д. На двусторонних (красных / желтых) счетчиках в котором не появляются две красные фишки подряд.

Экспериментально можно сделать вывод, что один счетчик можно расположить двумя способами, два счетчика – тремя способами, три счетчика – пятью и четыре счетчика – восемью (рис. 1). В частности, на рисунке 1 показано, что все комбинации с четырьмя счетчиками можно подсчитать путем рекурсивного сложения 3 + 5 = 8, поскольку их можно разделить на две группы, так что в первой группе (с мощностью три) крайний правый счетчик равен красный, а во второй группе (мощность пять) крайняя правая фишка желтая.Реализуя эту идею под руководством учителя, молодой ученик может обнаружить, что следующая итерация (пять счетчиков – 13 способов, так как 13 = 5 + 8) согласуется с описанием на рисунке 1. Увеличение для единообразия последовательность 2, 3, 5, 8, 13 двумя единицами (при условии, что пустой набор счетчиков имеет только одно расположение) позволяет описать завершение вышеупомянутого сценария обучения действиям (то есть отражения результатов воздействия на конкретный материалов согласно определенному правилу) через последовательность 1, 1, 2, 3, 4, 5, 8, 13,…, (в которой первые два числа равны единице, а каждое число, начиная с третьего, является суммой два предыдущих числа) – одна из самых известных числовых последовательностей во всей математике, названная в честь Фибоначчи (1270–1350), самого выдающегося итальянского математика своего времени.В рамках размышления над сценарием молодым студентам можно сказать, что, какими бы эзотерическими ни казались числа Фибоначчи, они, вероятно, столкнутся с ними снова.

Действительно, на вторичном уровне числа Фибоначчи можно исследовать в терминах отношений двух последовательных членов. С этой целью можно использовать электронную таблицу, чтобы продемонстрировать, что отношения приближаются к числу 1,61803 по мере увеличения n , независимо от первых двух членов последовательности, и. Точное значение, число, известное как золотое сечение.Это пример того, как использование компьютера может предоставить ученикам и их учителям неформальный мост, соединяющий более низкий когнитивный уровень с более высоким. Без простоты вычисления соотношений двух последовательных чисел Фибоначчи, представленных в электронной таблице, было бы намного труднее связать простую обучающую деятельность по конкретному расположению двусторонних счетчиков с когнитивно более сложной идеей сходимости отношения к числу, известному с древности как золотое сечение.Золотое сечение, мотивируемое компьютером, может быть обнаружено в контексте изучения специальной числовой последовательности, описывающей задачу обучения действиям, подходящую для маленьких детей. Другими словами, компьютер может естественным образом открыть окно для будущего практического обучения учащихся (см. Примечание об исследовании болезни Альцгеймера в Разделе 6 ниже).

В связи с использованием двусторонних счетчиков в контексте чисел Фибоначчи следует отметить, что многие кандидаты в учителя считают, что конкретные материалы можно использовать только на элементарном уровне, а выше этого уровня они бесполезны.Имея это в виду, авторы хотели бы утверждать, что, как и в случае с числами Фибоначчи, конкретные материалы могут использоваться для введения довольно сложных концепций, чтобы добавить фактор конкретности в изучение абстрактных идей. В частности, двусторонние счетчики могут служить воплощением двоичной арифметики во вводном курсе информатики. Более конкретно, если записать первые 16 натуральных чисел в двоичной форме, то при поддержке двусторонних счетчиков можно увидеть следующее.Есть два однозначных числа, в которых в ряду не появляются никакие единицы (без красных жетонов подряд), три двузначных числа без единиц, идущих подряд, пять трехзначных чисел, в которых в ряду не появляются никакие единицы, и восемь четырехзначных чисел, в которых подряд не встречаются единицы. Числа 2, 3, 5 и 8 – это последовательные числа Фибоначчи, которые, таким образом, могут быть использованы в качестве фрагментов предыдущих знаний учащихся при разработке новых идей посредством практического обучения. Для более подробных исследований вторичного (и третичного) уровня с числами Фибоначчи см. [43].

Очевидно, что мотивация связана с ожидаемым будущим успехом как следствие подросткового возраста. Теперь студенты стремятся к большей конкретизации понятий. Когда учащиеся средней школы имеют сильную мотивацию к практическому обучению, они могут создавать проекты уровня бакалавриата, как описано для студентов в Разделе 4.2 ниже. При «зрелой» работе над проектом постепенно появляется чувство «серьезности». Прекрасные примеры практического обучения учащихся средних школ, выступающих на уровне колледжа, можно увидеть на примере проекта Publix Лорен Вудбридж «Pallet Physics» ([44], v.3, 2 (8)), проект квантовых вычислений Бо Муна «Проблема суммы подмножеств: уменьшение временной сложности NP-полноты с помощью квантового поиска» ([44], т. 4, 2 (2)), ракетный проект Логана Уайта « Моделирование полета ракеты в приближении низкого трения »([44], v. 6, 1 (5)), и проект Рошана Вармана по спиновым вычислениям« Spintronic Circuits: The Building Blocks of Spin-based Computing »([44] , т. 7, 1 (1)).

4.1.2. Креативность и обучение действиям

Люди творческие, когда они мотивированы, и можно проявить больше творчества после общей, формирующей конкретизации идей.Важно рано распознавать творческие способности студентов. Педагоги рассматривают творчество как «один из важнейших навыков 21 века… жизненно важный для индивидуального и организационного успеха» ([45], стр. 1). Способность учителей распознавать творческие способности своих учеников, которые могут скрываться за их незрелой успеваемостью в классе, имеет решающее значение для успешного преподавания и продуктивного обучения. Если скрытые творческие способности учеников не признаются и не поддерживаются учителем, они, скорее всего, останутся бездействующими, а то и исчезнут [46].Следующая история, взятая из класса второго класса, поддерживает идею о том, что учителя являются главными хранителями раскрытия творческого потенциала маленьких детей.

Кандидат в учителя начальной школы, работая индивидуально с учеником второго класса (под наблюдением классного руководителя), попросил его построить все возможные прямоугольники из десяти квадратных плиток (настоящая проблема для второго класса), ожидая, что ученик Постройте два прямоугольника, 1 на 10 и 2 на 5, каждый из которых представляет собой факт умножения числа 10, что будет изучено позже (в третьем классе).Кандидат в учителя был удивлен, увидев три прямоугольника, как показано на рисунке 2. Большое количество обучающих идей для практического обучения может возникнуть из-за принятия прямоугольника с отверстием, которое демонстрирует скрытые творческие способности ребенка. Некоторые идеи могут быть связаны со вторичной математикой. Чтобы прояснить ситуацию, рассмотрите возможность изучения взаимосвязи между площадью и периметром этого прямоугольника с отверстием, считая как внешние, так и внутренние периметры (размышления под руководством учителя о действиях ученика с использованием конкретных материалов).Видно, что площадь составляет 10 квадратных единиц, а периметр – 20 погонных единиц. То есть численно периметр в два раза больше площади. Сравнение площадей с периметрами прямоугольников известно еще со времен Пифагора [47]. В режиме обучения действием можно исследовать следующую ситуацию: существуют ли другие прямоугольники с прямоугольными отверстиями, у которых периметр в два раза больше площади? С этой целью на уровне средней школы можно ввести четыре переменные: a , b , c и d , как длину и ширину большего и меньшего прямоугольников.Отсюда следует соотношение ab – cd = a + b + c + d . Используя Wolfram Alpha – вычислительную систему знаний, доступную бесплатно в Интернете, – можно попросить программу решить указанное выше уравнение над положительными целыми числами. В результате получится следующий результат:

Если задать a = b = 3, можно выбрать c = 1, откуда d = 1. Это дает нам квадрат с квадратным отверстием (рисунок 3).Этот пример показывает, как знание алгебры и возможности использования технологий могут помочь практикующим учителям в работе с маленькими детьми по развитию критического мышления и развитию творческих способностей. То есть, опять же, технологии служат неформальным мостом, который связывает между собой два разных уровня учебной программы по математике. Принимая во внимание, что учитель может не обязательно видеть богатую среду обучения за нетрадиционным ответом ученика, сам факт того, что такой ответ был принят и одобрен, будет мотивировать этого и других учеников продолжать мыслить нестандартно.

В заключение этого раздела отметим, что тройку, ученика начальной школы, классного учителя и кандидата в учителя, можно сравнить в контексте практического обучения с учеником бакалавриата, математическим факультетом и предметом. Area Adviser, как описано ниже в Разделе 4.2.2. Сходство двух сред (с разницей в несколько лет) заключается в двойном наблюдении за учеником, изучающим математику, дуэтом «более знающих других».

4.2. Бакалавриат по математике и практическому обучению

4.2.1. Понимание абстрактности с обучением на практике

Язык математики абстрактный с большей абстракцией на более высоких уровнях. Традиционно университетская математика для нематематических специальностей преподается, дистанцируясь от реальности, без связи с профессиональными интересами студентов. В этом контексте многие будущие профессионалы не видят важности математики в своих перспективных областях [48]. Кроме того, абстрактность в обучении часто приводит к проблемам в общении.Как отмечено в [49], в связи с преподаванием инженерной математики могут быть несоответствия между терминологией и идеями, используемыми математиком-преподавателем, и их интерпретацией студентами. Из-за того, что математическое образование на университетском уровне слишком теоретическое, оно становится неэффективным: нематематические специалисты изучают предмет «потому что они должны». Альтернативный подход к математическому образованию основан на хорошо известном и прагматичном понятии «обучение на практике» (например,ж., [50–54]), что делает возможным конструктивное взаимодействие чистых и прикладных идей. Этот подход имеет большой потенциал для внедрения экспериментального обучения в математический анализ – базовую последовательность курсов в учебной программе по высшей математике.

4.2.2. Математика Umbrella Model

Вся университетская учебная программа по математике для нематематических специальностей может извлечь выгоду из практического обучения. Было обнаружено, что, особенно на университетском уровне, следует придерживаться «середины пути» в отношении относительных весов, придаваемых теории и применению.Зонтичная группа математики (MUG) в Университете Южной Флориды (USF), инициированная Аркадием Гриншпаном в 1999 году [55], занимает эту «позицию». Он устраняет разрыв между математическим образованием и приложениями, одновременно вдохновляя студентов STEM на приобретение математических навыков, необходимых для успеха в соответствующих дисциплинах. Эта инициатива привела к разработке модели «Зонтик математики» в образовании STEM, включающей сотни междисциплинарных (прикладных математических) студенческих проектов.За десять лет, прошедших с момента сообщения о том, что программа MUG была первой организацией, которая содействовала персонализированным проектам по математике, при поддержке консультантов по математике и предметным областям, для обучения нематематических дисциплин студентам STEM [56], MUG оставалась уникальной в этом отношении. Каждый проект выполняется под двойным контролем: консультант по математике (математический факультет) и консультант по предметной области (университетский или общественный специалист), который обычно предлагает проблему [4, 48, 55, 57–59].

Отличительной чертой MUG является его уловка, объединяющая одного студента бакалавриата как минимум с двумя специалистами. Ситуация проиллюстрирована на Рисунке 4. В результате ученики получают доступ к более широкому кругу знаний, чем обычно предоставляется одному преподавателю математики.

Еще одна сильная сторона – это общность, которая возможна, или междисциплинарная связь, которая, по крайней мере, имеет место за пределами математического факультета вуза.Практическое обучение привносит «реальность» в абстракции математики. Даже когда преподаватели математики пытаются решить задачи с помощью приложений, полезность не осознается из первых рук, пока студенты не начнут применять ее. Это мотивационный подход для всех участников трио. Позже студенты могут решить провести исследование в связи с их опытом работы в проекте. Кроме того, они, вероятно, сохранят задействованные концепции дольше, чем при подходе «чистой лекции».

4.2.3. Практическое обучение на курсах математического анализа верхнего уровня

Практическое обучение является сильным мотивирующим фактором для всех участников, участвующих в математической группе Umbrella. Этот фактор, кажется, является общей нитью во всем спектре практического обучения K-20. Интерес участников к практическому обучению может быть пропорционален индивидуальному опыту. Преподаватели математики потенциально могут получить наибольшую пользу, но от студентов ожидается, что они будут знать теорию достаточно, чтобы их можно было мотивировать. Что касается программ бакалавриата по математике, таких как математический анализ II и III, считается, что студентам достаточно пройти несколько небольших тестов и домашних заданий, а затем направить свою энергию на практическое обучение, а не требовать от них успешной сдачи выпускного экзамена.В частности, эта педагогика практического обучения помогает студентам, которые «незначительно успешны», позволяя включать в их итоговые оценки компонент практического обучения, которому по праву придается значительный вес в общей оценке курса.

Чаще встречаются «успешные», которые могут быть очень продуктивными в своих проектах по обучению действиям. Есть вероятность того, что работы студентов будут опубликованы или, возможно, даже отмечены [4, 57], как и многие студенты за последние два десятилетия.Это прекрасные мотиваторы для всех сторон, участвующих в практическом обучении. Поскольку действие проистекает из мотивации, важно осознавать роль «мотиваторов действия». Для студентов высших учебных заведений мощный мотиватор часто заключается в том, чтобы узнать что-то полезное и что-то, на чем можно построить или улучшить успешную карьеру.

Примечательно, что студенты естественным образом мотивированы успехом в изучении математики. Влияние практического обучения было проанализировано в Университете Южной Флориды на курсах инженерного расчета, в которых участвовали тысячи студентов, прошедших эти курсы и последующие курсы с весны 2003 г. по весну 2015 г. [59].Некоторые результаты (сгруппированные по расе и этнической принадлежности) представлены на Рисунке 5 [59]. На этом рисунке показан эффект обучения действием, параллельных разделов обучения без действия и исторических (традиционных) разделов. В этой части исследования участвовали 1589 студентов, изучающих действие, и 1405 студентов, обучающихся на курсах, не использующих элемент обучения действием. Наконец, еще 2316 человек были помечены как «исторические», что означает, что они прошли курс до весны 2003 г. (то есть до того, как было проведено различие относительно использования или неиспользования практического обучения в своих курсах).Исследователи тщательно включили доверительные интервалы в свои результаты. Очевидно, что в этой относительно большой подгруппе из более крупного исследования все четыре категории расы / этнической принадлежности выступают за участие в практическом обучении. Для размышления есть много информации из [59]. Во всяком случае, этот и другие результаты демонстрируют академическое превосходство в действии над обучением без действия. Прагматический вывод состоит в том, чтобы обеспечить обучение действиям, поскольку с это работает.

4.2.4. Практическое обучение как универсальная образовательная концепция

Мотивация преподавателей математики возникает в результате знакомства с новым опытом практического обучения. В настоящее время зарегистрировано много сотен обучающих проектов, охватывающих широкий круг тем. Кроме того, всегда происходит обучение тонким действиям, которое никогда не документируется. Из тех проектов, которые доступны в Журнале бакалавриата по математическому моделированию: один + два (UJMM) [44], очевидно, что практически во всех областях можно использовать практическое обучение.Есть проекты, посвященные очень специфическим отраслям инженерии, например, биомедицинским нанотехнологиям. Есть также много других проектов, помимо «собственно инженерии», например, связанных с музыкой или даже образованием. Другие – это кросс-полевые типы, которые не поддаются четкой классификации. Типы мостов часто вызывают особый интерес. Это мотивирует преподавателей увидеть, что входит в смесь и какие области могут быть связаны посредством практического обучения. Это междисциплинарные особенности, желательные для всех учебных программ (в «вселенной учебных программ», то есть в образовании).Некоторые подробности доступны на главном веб-сайте Mathematics Umbrella Group (см. Центр промышленной и междисциплинарной математики). В журнале представлена ​​избранная подгруппа из более чем 2400 студенческих проектов, представленных с 2000 года. Указание на разнообразный характер тем проектов и участников студенческих работ очевидно из разнообразия предметов, рассматриваемых в последних заголовках UJMM ([44], v. 8 , 1-2): «Применение простых гармоник для моделирования толчка» Кая Раймонда, «Силы, действующие на парусную лодку» Келли Стукбауэр, «Оптимизация топливного элемента» Эдуардо Гинеса, «Анализ осадков в Тампе» Эми Полен, «Аппроксимация площади поверхности колеблющихся липидных листочков с использованием взвешенной сеточной мозаики» Анаф Сиддики, «Рудиментарная модель реакции глюкозы на стресс» Нашей Риос-Гусман, «Анализ органического сельского хозяйства: эффективность общепринятой практики» Брэдли Биега, «Использование Баланс скорости энтропии для определения теплопередачи и работы во внутренне обратимом, политрофическом, установившемся процессе потока »Саванна Гриффин,« Модельная функция улучшения мирового рекорда женщин на 1500 м с течением времени »Энни Аллмарк , «Максимальная мощность солнечного модуля из поликристаллического кремния» Джейнил Патель, «Оптимизация реакции сдвига водяного газа» Али Албулуши и «Волны цунами» Саманты Пеннино.

Помимо множества опубликованных проектов бакалавриата, существуют «сценарии практического обучения», которые можно рассматривать как совокупность различных практических занятий. Этот смешанный опыт имеет несколько идеалистических проблем. Проблемы можно считать типичными для того, что может рассматриваться в проекте, а не реальными примерами. Эти сценарии мотивируют преподавателя математики включать практическое обучение в обычный теоретический курс.Этим опытом, вероятно, поделятся любые преподаватели математики, занимающие аналогичные должности в математическом образовании. Непосредственной мотивацией здесь является расширение нашего понимания взаимосвязи между теорией математики и решением актуальных проблем в реальном мире.

5. Мотивирующие вопросы как основное средство изучения математики

5.1. Вопросы как инструменты обучения

Вопросы обычно становятся более сложными по мере взросления учащихся.Преподаватели на всех уровнях математического образования используют знания и опыт, чтобы ответить на вопросы. Желательны конкретные и уверенные ответы, при этом иногда (обычно на более высоких уровнях) вопросы могут потребовать дополнительного размышления перед их изложением. В контексте постановки проблем и их решения важно различать два типа вопросов, которые могут быть сформулированы так, чтобы стать проблемой: вопросы, требующие информации, и вопросы, требующие объяснения полученной информации [60].Подобно двум типам знаков – символам первого порядка и символике второго порядка [61] – можно относиться к вопросам, ищущим информацию, как к вопросам первого порядка, а те, которые требуют объяснения, как к вопросам второго порядка [46]. В то время как на вопросы первого порядка можно ответить, используя разные методы, похоже, что не все методы могут быть использованы для объяснения того, что было получено при поиске информации, то есть для предоставления ответа на вопрос второго порядка. Часто просьба о объяснении является разумным размышлением о методе предоставления информации.

Что означает, что учителя должны обладать «глубоким пониманием» математики? Зачем им нужно такое понимание? Есть несколько причин, по которым будущие учителя должны быть тщательно подготовлены к математике, чтобы иметь положительное влияние на успеваемость молодых изучающих математику. Во-первых, в современном классе математики ожидается, что ученики всех возрастов будут задавать вопросы, и их даже поощряют. В Соединенных Штатах национальные стандарты уже для классов до K-2 предполагают, что «необходимо воспитывать естественную склонность учащихся задавать вопросы… [даже] когда ответы не сразу очевидны» ([19], с.109). Это предложение подтверждается следующим комментарием кандидата в учителя начальной школы: «Не зная ответа на вопрос – это нормально, но нельзя оставлять этот вопрос без ответа». Кандидат описывает себя как «тот педагог, который всегда будет побуждать моих учеников задавать себе некоторые из тех же вопросов, которые позволят им участвовать в глубоком размышлении».

5.2. Международный характер обучения с помощью вопросов

На границе с США министерство образования Онтарио в Канаде в рамках своей учебной программы по математике для младших классов ожидает, что учителя будут иметь возможность «задавать учащимся открытые вопросы … поощряйте студентов задавать себе подобные вопросы… [и] моделируйте способы, которыми можно ответить на различные вопросы »([62], с.17). Для развития такого мастерства «учителя должны знать способы использования математических рисунков, диаграмм, манипулятивных материалов и других инструментов для освещения, обсуждения и объяснения математических идей и процедур» ([63], с. 33). В Чили учителя математики должны «использовать представления, опираться на предварительные знания, задавать хорошие вопросы и стимулировать любознательное отношение и рассуждение учащихся» ([64], с. 37). В Австралии учителя математики знают, как мотивировать «любопытство, бросить вызов мышлению учащихся, обсудить математический смысл и моделировать математическое мышление и рассуждения» ([65], с.4). Репертуар возможностей обучения, которые преподаватели предлагают своим ученикам, включает постоянный поиск альтернативных подходов к решению проблем, а также помощь ученикам в изучении конкретной стратегии решения проблем, с которой они боролись. В национальной учебной программе по математике в Англии используются такие термины, как «практика со все более сложными задачами с течением времени… [и] может решать задачи… с возрастающей степенью сложности» ([66], стр. 1). С этой целью учителя должны быть готовы иметь дело с ситуациями, когда естественный поиск вопросов приводит учеников к этой изощренности и усложнению математических идей.Необходимость такой подготовки учителей подтверждается кандидатом в учителя, который сформулировал это следующим образом: «Если ученик спрашивает, почему, а учитель не может объяснить, как что-то произошло, ученик теряет всякую веру и интерес к предмету и уважение к учителю ».

На уровне бакалавриата часто обсуждаются вопросы второго порядка. Преподаватели математики знают, что такие вопросы могут быть полезны для стимулирования дальнейших исследований. Возможно, правда, что математика, с которой приходится сталкиваться на уровне начальной и начальной школы, должна быть безупречно понята преподавателями математики и что учащиеся могут быть «уверены» в том, что им преподают.Когда мы начинаем заниматься, скажем, теорией множеств или двумерной / трехмерной геометрией, могут быть загадочные результаты, которые действительно побуждают учащихся задуматься об изучении высшей математики. Любопытство математики – это то, что учащиеся, вероятно, сочтут привлекательным. Конечно, преподавателю математики полезно иметь глубокое понимание темы; однако в ответе могут быть детали, которые не поддаются немедленному описанию. В некоторых редких случаях ответ даже не доступен. Ожидается, что зрелость студентов позволит им признать, что на более высоких уровнях математики они не должны терять веру и уважение к преподавателю, если объяснение откладывается.На более ранних этапах математического образования учащиеся верят, что математика идеальна. Однако математика так же несовершенна, как и все остальное, изобретенное людьми. Студенты должны это знать.

6. Компьютерная сигнатурная педагогика и модель обучения и преподавания 3P

Любопытство и мотивация также могут поддерживаться использованием цифровых инструментов в качестве инструментов практического обучения. Как было показано на примерах из дошкольного математического образования, компьютеры могут способствовать переходу с одного познавательного уровня на другой (более высокий).Это согласуется с современным использованием компьютеров в математических исследованиях, когда новые результаты возникают в результате вычислительных экспериментов. Например, радость перехода от визуального к символическому, когда двухсторонние счетчики были предложены как средство рекурсивного построения чисел Фибоначчи, которые затем можно было смоделировать в электронной таблице, где, возможно, благодаря интуиции, определился определенный образец в поведении соотношений могут быть обнаружены два последовательных члена. Это открытие мотивирует формальное объяснение того, почему отношения ведут себя определенным образом.Кроме того, переход от числового описания прямоугольников по периметру и площади приводит к их формальному представлению. В то время как прямоугольник с отверстием был обнаружен думать «из коробки», наличие цифрового инструмента облегчает переход от визуального к символическому с последующим использованием последнего представления в ситуации математического моделирования.

Мощность вычислительного моделирования может служить мотивацией для развития, а затем исследовать более сложные рекуррентные соотношения, чем у чисел Фибоначчи.Как обсуждалось в [58], использование моделирования в виде электронных таблиц может быть применено в контексте исследования болезни Альцгеймера для изучения популяции трансгенных мышей с упором на финансовую осуществимость покупки двух родительских мышей (самца и самку) и выращивания популяции мышей определенной размер. Эффективный подход к этой проблеме заключается в теории рекуррентных соотношений, которые первоначально были введены на вторичном уровне через числа Фибоначчи. Результаты, полученные с помощью моделирования в виде электронных таблиц, затем могут быть использованы для проверки теоретических результатов.Подробнее об этом проекте см. [55].

Все это приводит к понятию компьютерной сигнатурной педагогики (CASP), когда побуждает размышлять и поддерживать анализ действий, предпринятых учеником в контексте практического обучения, обеспечивает CASP глубинную (а не поверхностную) структуру обучения . [67] нанят учителем как «более знающий друг». Точно так же в более ранней публикации Биггс [15] проводил различие между поверхностной и глубинной структурой студенческих подходов к обучению , описывая первый подход в терминах студента, «вкладывающего минимальное время и усилия, чтобы соответствовать требованиям… [ тогда как последний подход] основан на интересе к предмету задачи; стратегия максимального понимания »(стр.6). Адаптировав модель обучения в классе, предложенную Данкином и Биддлом [68], Биггс [15] представил теперь известную 3P-модель обучения студентов, основанную на представлениях студентов об обучении в целом и их текущей учебной среде (прогноз), студенческий подход к обучению (процессу) и результат обучения студента (продукт). Исследование того, как первый P модели влияет на его второй P и, как следствие, третий P, было проведено Лиццио, Уилсоном и Саймонсом [69], которые выступили с семью теоретическими предложениями.Одно из этих предположений было основано на аргументе о том, что если студенты университетов воспринимают преподавание курсов их профессорами как надежное, то они с большей вероятностью выберут глубокий подход к обучению. Авторы пришли к выводу, что этот аргумент верен не только для учебных курсов по высшей математике, но и для курсов по методам математики для будущих школьных учителей. В современном преподавании математики правильное использование технологий является важной характеристикой учебной среды.В частности, в контексте студенческого подхода к обучению в глубокой структуре под эгидой CASP, можно расширить использование единого цифрового инструмента, такого как электронная таблица, другими современными технологиями, такими как Wolfram Alpha. С этой целью CASP, структурированный на основе глубоких подходов к преподаванию и обучению, может включать использование так называемых интегрированных электронных таблиц [70], которые поддерживают преподавание математики на всех образовательных уровнях с вычислительной надежностью обучения учащихся.

7.Проблемы и догадки, которые вдохновляют и мотивируют

Студент, изучающий математику (на любом уровне образования), вероятно, столкнется с «бесполезностью» математического совершенства. В математике есть легко выражаемые вопросы (предположения), на которые нет ответов (доказательство). Это похоже на принцип неопределенности Гейзенберга, где есть «пределы точности», например, при нахождении как положения, так и импульса. Важное понятие состоит в том, что не всегда есть «стандартные» решения математических задач.Зная это, учащиеся могут продолжить изучение математики для решения некоторых задач. В этих случаях действует «нестандартное» обучение действиям. Первоначальные размышления носят в основном теоретический характер, но в конечном итоге приложение будет вызвано. Заметьте, что проблему даже не нужно решать, многое предстоит узнать в этой попытке. Это мотивационный процесс. Кроме того, размышления привносят конкретность в концепции проблемы и относятся к общей «природе» проблем и решению проблем.

Реальные приложения математики в значительной степени стимулируют различные виды исследований в предметной области, в которых участвуют как профессиональные математики, так и студенты разных специальностей. Это не означает, что прикладная математика является единственным значимым источником развития математической мысли. Действительно, в самой математике есть много проблем, которые раньше мотивировали и продолжают мотивировать тех, кто стремится получить полное представление о математике как о фундаментальной науке.Некоторые из этих задач (иногда называемых предположениями) можно рекомендовать для включения в учебную программу по математике для не математических специальностей, а также для кандидатов в учителя. Опыт авторов показывает, что теоремы и предположения, берущие начало как в чистой, так и в прикладной математике, могут запустить воображение и мыслительный процесс тех, чей ум открыт для оспаривания.

Например, формулировки и исторические подробности таких захватывающих проблем, как Великая теорема Ферма, доказанная Эндрю Уайлсом [71], и гипотеза Бибербаха, доказанная Де Бранжем [72] (см. Также [73]), могут быть включены в некоторые базовые курсы математики. для нематематических специальностей.Доказательства этих теорем требуют не только элементарных средств, но и чрезвычайно сложны. Однако, как заметил Стюарт [74], «тот факт, что доказательство важно для профессионального математика, не означает, что преподавание математики данной аудитории должно ограничиваться идеями, доказательства которых доступны этой аудитории» (стр. 187). . Давайте взглянем на них.

Последняя теорема Ферма утверждает, что уравнение не имеет ненулевых целочисленных решений для x, y и z при .В частности, эта теорема может быть представлена ​​различным группам студентов-математиков как способ ответить на вопрос: Можно ли расширить интерпретацию троек Пифагора как разделение квадрата на сумму двух квадратов, чтобы включить аналогичные представления для более высоких степеней ? Как подробно описано в [75], использование электронной таблицы со второстепенными кандидатами в учителя позволяет визуализировать Великую теорему Ферма путем моделирования несуществующих решений вышеуказанного уравнения для почти таким же образом, как и для.Точно так же вполне возможно, что с помощью технологий или других средств естественный мост между утверждением Великой теоремы Ферма и некоторыми геометрическими свойствами модульных эллиптических кривых в доказательстве Уайлса станет доступным для будущих студентов-математиков.

Гипотеза Бибербаха утверждает, что для каждой аналитической функции, взаимно однозначной в единичном круге, неравенство выполняется. Один только этот легендарный результат с его потрясающими рекордами (см., Например, [76]) может пробудить интерес студентов к изучению таких важных математических понятий, как взаимно однозначные функции, степенные ряды, сходимость и коэффициенты Тейлора, которые, в частности, являются целесообразно обсудить с инженерами-майорами.Здесь также стоит упомянуть о глубоких геометрических корнях гипотезы Бибербаха. Например, его доказательство для основано на представлении плоской заданной области в виде контурного интеграла, и, таким образом, оно доступно для нематематических специальностей, зачисленных на курс исчисления верхнего уровня.

Существует также известная гипотеза Гольдбаха [77], которая утверждает, что каждое четное число больше двух может быть записано как сумма двух простых чисел (возможно, более чем одним способом). Было бы чудом, если бы эта гипотеза оказалась ложной.Пока встречных примеров не найдено. Хотя поиск противоположного примера кажется бесплодным, эмпирически было показано, что гипотеза Гольдбаха верна для всех четных чисел больше двух и меньше некоторого известного числа, состоящего из 17 цифр.

Еще одна известная, но легкая для понимания проблема – это гипотеза палиндрома [78]. Он имеет дело со свойством палиндромов (т. Е. Целых чисел, которые читаются так же, как вперед и назад) привлекать целые числа в соответствии со следующей процедурой: начать с любого целого числа, перевернуть его цифры и сложить два числа; повторите процесс с суммой и продолжайте видеть, что это приводит к палиндрому.Примечательно, что эта «игра с числами» недавно была упомянута как одна из двенадцати нерешенных проблем современной математики [79]. Именно эта проблема и, как отмечается в Принципах и стандартах школьной математики [19], ее образовательный потенциал для учащихся средних школ, позволяющий «оценить истинную красоту математики» (стр. 21), побудили кандидата в учителя средней школы работать с один из авторов по разработке вычислительных обучающих сред для учебных презентаций и экспериментов с большим классом развлекательных задач, как решенных, так и нерешенных [80].Как выразился Гаусс, «в арифметике наиболее элегантные теоремы часто возникают экспериментально в результате более или менее неожиданной удачи, а их доказательства лежат настолько глубоко погруженными в темноту, что опровергают самые острые вопросы» (цитируется в [81]. ], стр. 112).

Похоже, что использование технологий для значимых экспериментов с числами под эгидой CASP может вдохновить и мотивировать студентов уже на уровне дошкольного образования к новым открытиям в элементарной теории чисел.Каким-либо образом расширяя наше понимание математики, мы потенциально расширяем нашу способность «процветать». Это неотъемлемая ценность и мотивация для обучения действиям. Предполагается, что вся математика может иметь приложения. Нам нужно только иметь мотивацию для разработки этих приложений.

8. Заключение

В этой статье, используя опыт авторов в преподавании математики и надзоре за применением предмета в практике государственных школ и промышленности, представлена ​​структура совместного использования практического обучения и концептуальной мотивации в контексте К-20 математического образования.Были представлены различные примеры практического обучения – индивидуальная работа над реальной проблемой с последующим размышлением под наблюдением «более знающего другого». Такой надзор может включать в себя «дуэт других» – классного учителя и кандидата в учителя в школе K-12, а также преподавателя математики и советника по предметной области в университете. В документе показано, что практическое изучение математики идет рука об руку с концептуальной мотивацией – методикой обучения, в которой введение математических концепций мотивируется (соответствующими классу) реальными приложениями, которые могут включать в себя действия учащихся над объектами, ведущие к формальному описанию этого. действие через символику математики.Этот подход основан на важных рекомендациях математиков [5, 16, 17] и педагогических психологов [1, 25, 26, 61].

Главный вывод статьи состоит в том, что за счет многократного использования концептуальной мотивации и практического обучения на всех уровнях математического образования общий успех учащихся имеет большой потенциал для улучшения. Это сообщение подкреплено примерами творческого мышления молодых учащихся в классе, основанного на всестороннем сотрудничестве школьных учителей и преподавателей университета (в духе Группы Холмса [82]).Точно так же это сообщение было подкреплено примерами интереса студентов к изучению математического анализа посредством практического обучения в реальных условиях. Похоже, что растущий интерес студентов к математике связан с практическим обучением и концептуальной мотивацией, которые использовались для исправления широко распространенного формализма в преподавании математики, который, в частности, стал препятствием на пути к успеху STEM-образования [4, 7, 8] . Когда учащиеся имеют опыт практического изучения математики в школьные годы, они, вероятно, продолжат изучение предмета в том же духе, тем самым избежав многих препятствий на пути перехода от среднего образования к высшему.Как упоминалось в разделе 4.2.3, исследование по внедрению практического обучения инженерному исчислению с участием тысяч студентов Университета Южной Флориды [4, 59] показывает, что, хотя интерес студентов к практическому обучению может быть пропорционален индивидуальному опыту в этом случае их результаты обучения демонстрируют академическое превосходство практического обучения над другими педагогическими средствами проведения расчетов.

В начале формального математического образования школьники должны начать знакомство с педагогикой практического обучения и концептуальной мотивации, усиленной, в зависимости от обстоятельств, задаванием вопросов и ответами на них, а также обучением использованию технологий.Как было показано в документе, не только учебные программы по математике K-12 во многих странах поддерживают обучение учащихся, задавая вопросы, но и их будущие учителя ценят такой вид математического обучения. Аналогичным образом, компьютерная педагогика с использованием сигнатур [37] может быть использована для максимального понимания учащимися математики и поощрения их глубокого подхода к обучению [15]. У студентов университетов больше мотивации, чем у школьников, чтобы справляться с обязанностями взрослой жизни. Тем не менее, обе группы студентов все еще могут быть мотивированы своим естественным «бросающим вызов возрасту» любопытством.В этом отношении стимулирующие вопросы, склонность к использованию компьютеров и известные классические задачи являются важными инструментами мотивации при изучении математики. Объединение всей учебной программы по математике K-20 в единое целое возможно, когда методы концептуальной мотивации и обучения действиям используются во всем этом образовательном спектре. Наконец, очевидно, что есть прагматическая причина для того, чтобы знакомить учащихся с радугой обучения действию, и это потому, что среди сегодняшних учеников есть завтрашние учителя.Процесс должен и дальше развиваться.