Шкала перевода первичных баллов в оценки (ЕГЭ-2018 по математике, профильный уровень)
Система оценивания на ЕГЭ по математике профильного уровня существенно сложнее. Во-первых, экзаменационные задания имеют разную “цену”. Задания из первой части (с кратким ответом) наиболее “дешевы”; самыми “дорогими” являются последние две задачи (уравнение или неравенство с параметром и задача по теории чисел).
| Номер задания | Максимальное количество баллов |
| 1 – 12 | 1 |
| 13 – 15 | 2 |
| 16, 17 | 3 |
| 18, 19 | 4 |
В 2018 году идеальное решение всех девятнадцати заданий может принести 32 первичных балла.
Первичные баллы переводятся в тестовые баллы. Шкала перевода незначительно изменяется от года к году.
ЕГЭ по математике (профильный уровень). Шкала перевода первичных баллов в тестовые баллы| Первичный балл | Тестовый балл |
| 0 | 0 |
| 1 | 5 |
| 2 | 9 |
| 3 | 14 |
| 4 | 18 |
| 5 | 23 |
| 6 | 27 |
| 7 | 33 |
| 8 | 39 |
| 9 | 45 |
| 10 | 50 |
| 11 | 55 |
| 12 | 59 |
| 13 | 64 |
| 14 | 68 |
| 15 | 70 |
| 16 | 72 |
| 17 | 74 |
| 18 | 76 |
| 19 | 78 |
| 20 | 80 |
| 21 | 82 |
| 22 | 84 |
| 23 | 86 |
| 24 | 88 |
| 25 | 90 |
| 26 | 92 |
| 27 | 94 |
| 28 | 96 |
| 29 | 97 |
| 30 | 98 |
| 31 | 99 |
| 32 | 100 |
| 33 | 100 |
| 34 | 100 |
ЕГЭ не сдан, если набрано менее 27 баллов.
Начало. Шкала перевода баллов на ЕГЭ базового уровня →
Успешно сдать профиль ЕГЭ по математике: советы эксперта
Сергей Сергеевич Леонов, кандидат физико-математических наук, старший преподаватель по высшей математике в МАИ, ведущий также подготовительные курсы при университете, подготовил для абитуриентов МАИ советы, которые помогут успешно сдать профильный ЕГЭ и поступить в выбранный вуз.
Результаты сдачи абитуриентами профиля по математике в 2017 году
Средний балл по профильной математике на ЕГЭ составил 47,1. Для сравнения, в 2016 году средний балл был равен 46,3, а в 2015 — 45,6. При этом, процент не сдавших профильный ЕГЭ по математике снизился за год с 4,6 до 3,4. Разные источники озвучивают разные данные, но все отмечают рост среднего балла в 2017 году.
Результаты профильной математики не стали хуже. Это можно связать с тем, что с 2015 года не было серьёзных изменений в процедуре сдачи ЕГЭ по математике. Это положительно влияет на подготовку к ЕГЭ. Думаю, если ситуация с ЕГЭ останется стабильной, то со временем средний балл стабилизируется в районе некоторого значения.
Думаю, если ситуация с ЕГЭ останется стабильной, то со временем средний балл стабилизируется в районе некоторого значения.
Проходной балл по математике в МАИ
Минимальный балл по математике, с которым принимаются документы в Московский авиационный институт в 2017 году, составил 39 баллов. Но стоит учитывать, что минимальный суммарный балл в 2017 году по инженерным специальностям составил в среднем 190-210 баллов, редко опускаясь до 170-180. А на физико-математических специальностях, таких как прикладная математика, и специальностях, связанных с информационными технологиями, таких как прикладная математика и информатика, информационная безопасность и т. д., средний суммарный балл равен 220-230 и может достигать 260. Сравнивая эти значения с баллами за 2013-2016 гг., можно отметить, что в 2017 году минимальный суммарный балл вырос в среднем на 10-20 баллов.
Прогнозируя минимальные баллы на 2018 год, стоит учитывать, что за последние годы МАИ неизменно занимает высокие позиции в российских и международных рейтингах наряду с ведущими российскими техническими вузами. Более того, МАИ сотрудничает со многими профильными компаниями аэрокосмической отрасли и иностранными университетами. Всё это делает МАИ привлекательным для абитуриентов.
Более того, МАИ сотрудничает со многими профильными компаниями аэрокосмической отрасли и иностранными университетами. Всё это делает МАИ привлекательным для абитуриентов.
И можно ожидать, что конкурс в 2018 году будет только расти, а значит и минимальные вступительные баллы будут не меньше, чем в 2017 году. Суммируя все сказанное, для успешного поступления в МАИ в 2018 году необходимо для инженерных специальностей набрать не менее 60-65 баллов по математике, а для физико-математических и IT-специальностей — не менее 75-80 баллов.
Что ждёт абитуриентов 2018 года при сдаче ЕГЭ по профильной математике?
Насколько мне известно, существенных изменений в вариантах и процедуре сдачи ЕГЭ по математике, по сравнению с 2017 годом, не будет. Профильный уровень по математике состоит из двух частей, общее количество заданий — 19. В первой части 8 заданий с указанием ответа, во второй части 4 задания (9-12) с указанием ответа и 7 заданий (13-19) с развёрнутым ответом.
Задания первой части рассчитаны на базовый уровень, во второй части даются задания, рассчитанные на углублённое изучение математики. Максимальное количество первичных баллов, которые потом пересчитываются в стобалльную шкалу, равно 32. За успешное выполнение каждого задания первой части даётся по одному баллу, то же и для 9-12 заданий второй части. Выполнение заданий 13-15 принесёт по 2 балла, 16-17 — по 3 балла, 18-19 — по 4 балла. Для получения 60 баллов в стобалльной шкале необходимо получить не менее 11-12 первичных баллов, а для 70 — не менее 14.
Максимальное количество первичных баллов, которые потом пересчитываются в стобалльную шкалу, равно 32. За успешное выполнение каждого задания первой части даётся по одному баллу, то же и для 9-12 заданий второй части. Выполнение заданий 13-15 принесёт по 2 балла, 16-17 — по 3 балла, 18-19 — по 4 балла. Для получения 60 баллов в стобалльной шкале необходимо получить не менее 11-12 первичных баллов, а для 70 — не менее 14.
Хотелось бы пару слов сказать об оформлении экзаменационной работы. Экзаменационные бланки ЕГЭ требуют специального способа заполнения. При первом столкновении с экзаменационными бланками у учащихся могут возникнуть трудности с записью ответа, его исправлением или заменой. Каждому учащемуся советую заранее ознакомиться с видом бланков ЕГЭ, порядком записи и исправления ответа, а при записи ответа проявлять максимальные аккуратность и внимательность. Будет очень обидно из-за неаккуратности потерять даже один балл. Также можно рекомендовать хотя бы один раз сдать пробный экзамен.
Эффективная подготовка к профилю по математике
По моему мнению, эффективная подготовка к экзамену должна сочетать проработку теории, систематическое решение и разбор задач различного уровня сложности и периодическую диагностику знаний. Существует масса пособий и электронных ресурсов, посвящённых ЕГЭ. Но, советую критически относится к каждому из них, в особенности к материалам, размещённым в интернете. Данные в интернете публикуются зачастую анонимно и трудно определить их содержательность и правильность.
Лучше пользоваться электронными ресурсами, предоставляемыми официальными структурами. Например, стоит начать с сайта Федерального института педагогических измерений (ФИПИ, www.fipi.ru). На нём даны основные нормативные акты, банк заданий ЕГЭ, демонстрационные варианты. Из печатных изданий стоит ориентироваться на те, которые соответствуют новому ФГОС (федеральному государственному образовательному стандарту).
Для подготовки можно посоветовать серию книг «ЕГЭ 2018. Математика» под редакцией И. В. Ященко. Каждая книга этой серии посвящена одному номеру задачи ЕГЭ и содержит диагностические работы, а также дифференцированные варианты по каждому встречающемуся типу задач.
Математика» под редакцией И. В. Ященко. Каждая книга этой серии посвящена одному номеру задачи ЕГЭ и содержит диагностические работы, а также дифференцированные варианты по каждому встречающемуся типу задач.
Если отойти от ЕГЭ, то в качестве сборников задач можно рекомендовать:
1. Сборник задач по математике для поступающих во ВТУЗы / под ред. М. И. Сканави. М.: Изд-во АСТ, 2017.
2. Шарыгин И. Ф. Решение задач. М.: Просвещение, 1994.
По алгебре советую обратить внимание на книги:
1. Нелин Е. П. Алгебра. 7-11 классы. М.: Илекса, 2014.
2. Вавилов В. В. и др. Задачи по математике. Уравнения и неравенства. М.: Наука, 1987.
3. Азаров А. И. и др. Алгебраические уравнения и неравенства. Ч. 1 и 2. Минск: Тривиум, 1997.
4. Кочетков Е. С., Кочеткова Е. С. Алгебра и элементарные функции. Ч. 1 и 2. М.: Просвещение, 1969.
В качестве дополнительной литературы по геометрии, в особенности для учащихся, нацеленных на высокие баллы по ЕГЭ, будут полезны следующие книги:
1. Нелин Е. П. Геометрия. 7-11 классы. М.: Илекса, 2014.
Нелин Е. П. Геометрия. 7-11 классы. М.: Илекса, 2014.
2. Киселев А. П. Геометрия. М.: Физматлит, 2004.
3. Прасолов В. В. Задачи по планиметрии. М.: Наука, 1991.
4. Прасолов В. В., Шарыгин И. Ф. Задачи по стереометрии. М.: Наука, 1989.
5. Калинин А. Ю., Терешин Д. А. Геометрия. 10-11 классы. М.: МЦНМО, 2015.
Нет необходимости использовать при подготовке все указанные пособия, но, несомненно, обращение к каждой из них позволит учащемуся пополнить свои знания и лучше подготовиться к экзамену.
Что касается самой подготовки, то успешные абитуриенты готовятся систематически и заранее. Вопрос о том, как именно готовиться к ЕГЭ, является индивидуальным. Для многих школьников качественные самостоятельные занятия приносят хорошие плоды. А в ряде случаев и занятия с репетиторами не приводят к желаемым результатам. Все зависит от желания учиться.
Традиционно физико-математические школы и классы с углублённым изучением математики дают хорошую подготовку к экзамену, также можно воспользоваться долгосрочными курсами в технических вузах. Но стоит осознавать, что нужно качественное образование, а не «натаскивание» на задания экзамена, иначе будет трудно адаптироваться в институте.
Но стоит осознавать, что нужно качественное образование, а не «натаскивание» на задания экзамена, иначе будет трудно адаптироваться в институте.
Типичные ошибки абитуриентов
Как бы это банально не звучало, но типичными являются арифметические ошибки, появляющиеся из-за невнимательности при расчётах. Но элементарная проверка решения позволяет избавиться от большинства подобных ошибок. Поэтому важно понимать, что проверка — это неотъемлемая часть процесса решения.
Также часто встречаются ошибки, связанные с не учётом или неправильным определением области допустимых значений, определением возможных исходов в задачах теории вероятностей, решением уравнений и неравенств с модулем и параметрами. При решении математических задач недостаточно знать формулы, теоремы и свойства, необходимо также иметь навыки решения задач, для чего нужно систематически решать задачи различного уровня сложности.
Ярким примером являются геометрические задачи. Довольно часто, учащиеся, зная необходимые теоремы, затрудняются решить задачи геометрии, потому что не знают с чего начать решение или не могут начертить удобный рисунок. При подготовке к экзамену стоит уделять внимание задачам разного уровня сложности. Даже если сложные задачи не даются сразу, со временем они буду решаться легче. Также можно рекомендовать время от времени выполнять диагностические работы, чтобы видеть на какие типы задач стоит обратить внимание в первую очередь.
При подготовке к экзамену стоит уделять внимание задачам разного уровня сложности. Даже если сложные задачи не даются сразу, со временем они буду решаться легче. Также можно рекомендовать время от времени выполнять диагностические работы, чтобы видеть на какие типы задач стоит обратить внимание в первую очередь.
Можно ли успеть «подтянуть» свои знания до начала экзаменов?
За те 4-5 месяцев, что остались до экзамена, как мне кажется, не удастся серьёзно поднять свою оценку. Скажем, со слабой тройки добраться до пятерки. Это очень редкий случай. Многие компании и учебные центры манипулируют страхом провала на экзамене и в последние месяцы перед ЕГЭ устраивают краткосрочные курсы, обещая замечательные результаты вне зависимости от уровня ученика. Во многих случаях это обман и стоит относиться к таким предложениям с осторожностью.
Более реальный вариант — это максимальная ликвидация пробелов в знаниях. Вполне реально поднять свой результат на несколько десятков баллов. Трудно сказать на каких конкретно типах задач стоит концентрироваться учащимся, у каждого ученика могут быть свои проблемные точки. Если уровень знаний невысокий, то следует основное внимание уделять подготовке к первой части ЕГЭ и заданиям 9-12 второй части.
Трудно сказать на каких конкретно типах задач стоит концентрироваться учащимся, у каждого ученика могут быть свои проблемные точки. Если уровень знаний невысокий, то следует основное внимание уделять подготовке к первой части ЕГЭ и заданиям 9-12 второй части.
Задачи первой части рассчитаны на общеобразовательный уровень. Как правило, задания первой части легко выполнить правильно, заработав базовое количество баллов, которое можно увеличить, решая наиболее понятные ученику задачи второй части. Подробно при подготовке следует рассмотреть геометрические задачи по планиметрии и стереометрии, так как ряд задач первой и второй части ЕГЭ посвящён именно геометрии. Наибольшие трудности могут возникнуть с задачами по геометрии из второй части. Часто недостаточно просто знать теоретические сведения из курса геометрии.
Существенной частью является поиск подхода к решению задачи, рисунок, от этого зависит успешное решение. Поэтому как можно раньше нужно вырабатывать навыки геометрических построений и рассуждений. Многие задания второй части ЕГЭ, в особенности задания 13-19 с развёрнутым ответом, могут представлять трудности для слабо подготовленного ученика. Но не стоит опускать руки. Систематическое решение разных по типу и сложности задач позволит если не полностью выполнить все задания второй части, то, наверняка, получить несколько лишних баллов, которые могут оказаться необходимыми при поступлении.
Многие задания второй части ЕГЭ, в особенности задания 13-19 с развёрнутым ответом, могут представлять трудности для слабо подготовленного ученика. Но не стоит опускать руки. Систематическое решение разных по типу и сложности задач позволит если не полностью выполнить все задания второй части, то, наверняка, получить несколько лишних баллов, которые могут оказаться необходимыми при поступлении.
Сдать профиль на 100 баллов: насколько это реально?
Высокие баллы по математике на ЕГЭ вполне реальны. Но подготовка к экзамену должна быть комплексной. Каждая задача ЕГЭ посвящена определённому разделу математики. Не редки случаи, когда школьники стараются запомнить алгоритм решения конкретных задач, которые встречаются в пробных и демонстрационных версиях. А на экзамене, получая задачи другого типа или вида, они теряются, начинают нервничать, даже если хорошо подготовились.
Правильным путём подготовки является не «натаскивание» на отдельные типы задач, а усвоение общих приёмов и подходов при интенсивной практической работе по решению задач различного уровня сложности.
Как подготовка к ЕГЭ пригодится абитуриенту в учёбе
Качественная подготовка к ЕГЭ и его успешная сдача, безусловно, дают хорошую базу для усвоения университетского курса высшей математики. Однако корреляции между успешной сдачей ЕГЭ и успешным обучением в вузе нет, так как в образовании помимо уровня знаний присутствует ещё множество факторов.
Стоит сразу же предостеречь абитуриентов: как бы хорошо не были сданы экзамены, не следует расслабляться, необходимо сразу же активно вливаться в учебный процесс. Не редки случаи, когда студенты, поступившие в вуз со средними баллами, за счёт усидчивости и трудолюбия достигают значительных успехов в учёбе. В особенности это касается математических дисциплин. В тоже время, сильным абитуриентам, затянувшим с отдыхом после сдачи ЕГЭ, труднее влиться в учебный процесс.
Но запас знаний это не единственное, что влияет на успешную учёбу в институте. Гораздо большее влияние на студентов оказывают преподаватели, которые должны зажечь интерес к предмету и помочь студентам найти себя в профессии.
Как преподаватель МАИ, в течение ряда лет ведущий лекционные и практические занятия по математическим дисциплинам, могу сказать, что в МАИ преподаватели с вниманием и лояльностью относятся к студентам, прикладывая много сил для того, чтобы студенты получили качественное образование. Будущим студентам хочу посоветовать, не стесняться задавать вопросы преподавателям. Ведь только установив двухстороннюю связь между студентом и преподавателем можно добиться наилучших результатов.
Источник: mai.ru
Всё “слитое” стало явным. Результаты ЕГЭ дошли до школьников : Аналитика Накануне.RU
Всё “слитое” стало явным. Результаты ЕГЭ дошли до школьников
По профильной математикеВсе участники ЕГЭ по профильной математике получили свои результаты. Вместе с раскладкой по баллам в личном кабинете выложены сканы бланков №2, на которых школьники решали задачи с развернутым ответом. Даже беглого сравнения условий задач, которые попались ребятам на экзамене, с теми, которые выложили накануне в интернет, достаточно, чтобы установить их сходство. Некоторые задачи, действительно, были доступны в сети до ЕГЭ, передает корреспондент
Задачи на цилиндр, окружность и трапецию сравнить с выложенными в сеть было проще всего.
Задание №14 на цилиндр отличается от варианта из интернета только цифрами, условия обоих экзаменационных вариантов те же.
В условии экзаменационной задачи на окружность отличается разве что сочетание вершин параллелограмма, через которые проходит окружность. Суть задания это не меняет.
Условие и первый вопрос задания №16 один в один совпадает с заданиями со страницы педагога Дмитрия Гущина. Правда, судя по ответу участника ЕГЭ, у задачи был и второй вопрос, который не был указан в выложенных вариантах. И это упущение неслучайно, предположил доктор физико-математических наук, профессор из Петрозаводска Александр Иванов.
“Среди заданий Гущина есть такие, которые не имели никаких аналогов среди материалов “открытого доступа”. Например, задачи 16.1 и 16.2. Их текст до запятой совпал с тем, что получили многие школьники на ЕГЭ 1 июня. Но обратите внимание, условия этих задач у Гущина неполные, там отсутствует пункт б), который был на экзамене. Почему же организаторы “слива” исключили этот пункт? Получается интересная ситуация. С одной стороны, первоисточник “списка Гущина” очевиден – недра ФИПИ, но качество представленных материалов явно хромает. С другой – Кравцов и Ященко публично клянутся, что “тождественных совпадений” заданий списка с реальными КИМами нет.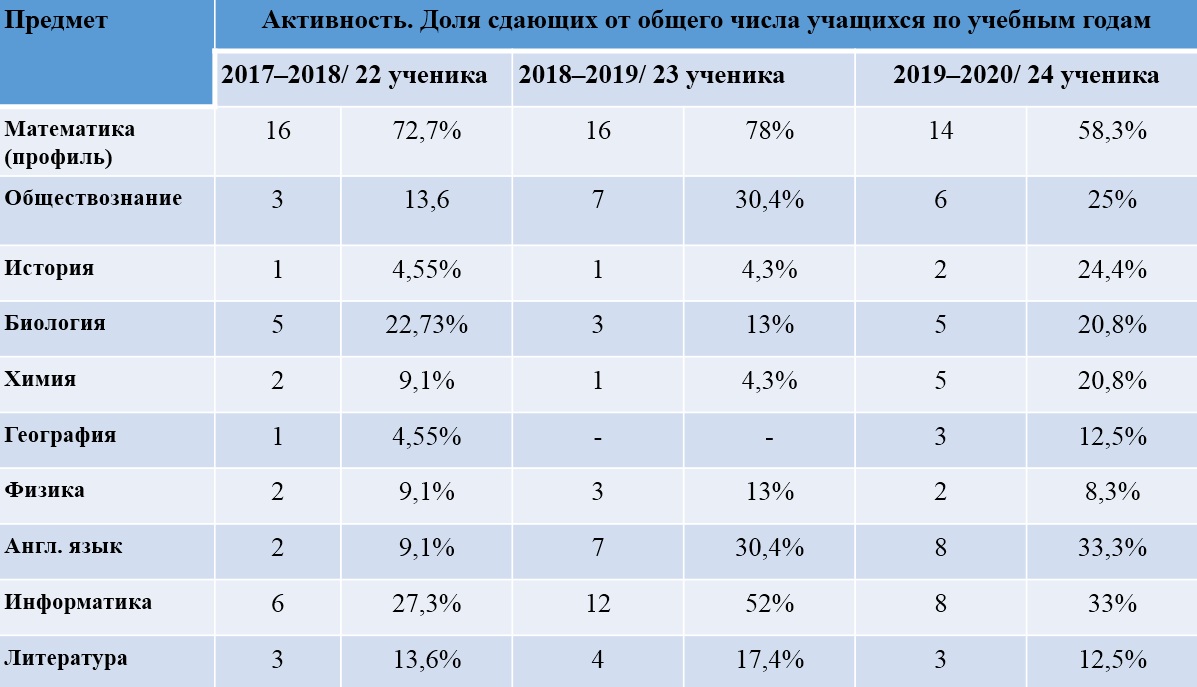
А вот экономическая задача с “инсайдерской” не совпала, утверждает разработчик ЕГЭ Иван Ященко. По его словам, многие выпускники не смогли решить ее из-за натаскивания педагогов и репетиторов на прошлогодние варианты и демо-версию.
“Условие было абсолютно типовое, мы показывали, что те задания, которые якобы были слиты в сети интернет, это варианты из книг, из открытого банка. В реальном экзамене
вопрос был немного другой. Не как в прошлом году и не как в этих вариантах. Коллеги, проверяющие ЕГЭ, подтверждали, что, к сожалению, увеличилось количество ребят, которые, практически игнорируя условие, решали задачу по типовому алгоритму. В результате у нас по этой задаче сократился процент выполнения на полный балл. Это косвенно подтверждает, что никакого слива не было, ведь после этого бы [процент выполнения задачи] вырос”, – рассказал Иван Ященко в прошлый четверг на конференции в ситуационно-информационном центре Рособрнадзора.
В результате у нас по этой задаче сократился процент выполнения на полный балл. Это косвенно подтверждает, что никакого слива не было, ведь после этого бы [процент выполнения задачи] вырос”, – рассказал Иван Ященко в прошлый четверг на конференции в ситуационно-информационном центре Рособрнадзора.
Условия 17-й задачи появились вместе с остальными заданиями на портале по подготовке к ЕГЭ. “Задания составлены нами со слов самих участников ЕГЭ-2018 и публикуются строго после экзамена в ознакомительных целях”, – говорится в описании на сайте.
Проверить совпадение этого задания со “слитым” по ответам учеников оказалось непросто: условия задачи на бланках приводятся не так наглядно, как в предыдущих случаях.
Задачи с 13 по 19 ЕГЭ по профильной математике считаются сложными. За правильное решение одного такого задания начисляется от двух до четырех баллов, которые при пересчете на 100-балльную шкалу могут обеспечить участнику значительное преимущество. Так что в случае утечки даже прототипа задания школьник может заранее подготовиться к выполнению самых трудных испытаний.
Так что в случае утечки даже прототипа задания школьник может заранее подготовиться к выполнению самых трудных испытаний.
Напомним, накануне ЕГЭ по профильной математике петербургский педагог Дмитрий Гущин, получивший звание “Учитель года” в 2007 г., заявил о предполагаемых утечках заданий на своей странице “Вконтакте”. В подлинности “слитых” в сеть прототипов убедились сотни школьников со всей страны и эксперты, проверяющие “творческую часть” их работ.
Правда, ни Рособрнадзор, ни Федеральный институт педагогических измерений (ФИПИ) утечку заданий ЕГЭ по профильной математике не подтвердили.
“Мы взяли все задачи, которые были опубликованы в интернете, и сверили их с базой реальных заданий. Никаких утечек, как в 2013 г., когда в интернете появлялись оригинальные материалы, в этом году не было! Были лишь отдельные аналогичные задания”, – заявил глава Рособрнадзора Сергей Кравцов.
Руководитель группы разработчиков заданий по математике Ященко утверждает, что аналоги заданий несложно было найти в демо-версиях или задачах прошлых лет. “Ни одно из [выложенных Гущиным] заданий не тождественно реальным”, – заявил директор центра педагогического мастерства и глава разработчиков заданий по математике Иван Ященко.
И все же, если утечка произошла и часть школьников оказалась лучше подготовлена к решению экзаменационных задач, чем другие, принцип справедливости ЕГЭ нарушился.
За восстановлением справедливости президент Всероссийского фонда образования, доктор педагогических наук Сергей Комков посоветовал родителям обратиться в Генпрокуратуру.
“Мой совет родителям достаточно прост: им немедленно надо через кого-то из депутатов Государственной думы направить официальное заявление в Генпрокуратуру России с требованием разобраться с данной ситуацией, провести экспертизу и, вероятно, по ее результатам возбудить уголовные дела в отношении конкретных официальных лиц в Рособрнадзоре, ответственных за организацию и проведение ЕГЭ в 2018 г. По какой конкретно статье УК РФ, пусть определят следователи”, – отметил Сергей Комков в разговоре с Накануне. RU.
RU.
В свою очередь Рособрнадзору, по его мнению, следует признать результаты ЕГЭ по профильной математике в этом году недействительными и аннулировать их, чтобы исключить возможность манипуляции результатами данного экзамена.
“Без подобного рода жестких мер фальсификации и манипуляции с ЕГЭ не прекратятся никогда! Но повторяю уже в сотый раз! Пока вообще будет существовать система ЕГЭ, на мой взгляд, будет существовать и процветать система махинаций и коррупции в сфере российского образования! Гнилое дерево надо рубить под корень!” – заключил Сергей Комков.
Александр Иванов напомнил, что каждый, кто считает себя потерпевшим в этой истории, имеет право подать в суд “с требованием компенсации моральных и материальных (бюджетные места) потерь”.
Напомним, профессор Александр Иванов обратился к депутатам Госдумы с просьбой создать специальную комиссию для расследования предполагаемой утечки прототипов заданий ЕГЭ по профильной математике, которая определила бы виновных и устранила их от управления образованием.
ЕГЭ 2022. Профильный экзамен по математике станет сложнее
В 2020 году произошли существенные изменения в структуре контрольно-измерительных материалов ОГЭ по математике в 9‑м классе. Эти изменения были необходимы для того, чтобы привести экзаменационные задания в соответствие с действующими стандартами ФГОС. Прошло два года, и мы, учителя математики, с нетерпением ждали демонстрационной версии профильного экзамена по математике, чтобы оценить, насколько изменится структура экзаменационной работы в этом учебном году по сравнению с предыдущими. Ведь на протяжении большого количества лет структура КИМов профильного ЕГЭ по математике не менялась.
Изменения действительно произошли, и можно с уверенностью утверждать: профильный экзамен по математике станет сложнее, потому что из работы удалены первые самые легкие задания – задачи 1 и 2, проверяющие умение использовать приобретенные знания и умения в практической и повседневной жизни (уровень 5-6-х классов), и задание 3, проверяющее умение выполнять действия с геометрическими фигурами, координатами и векторами.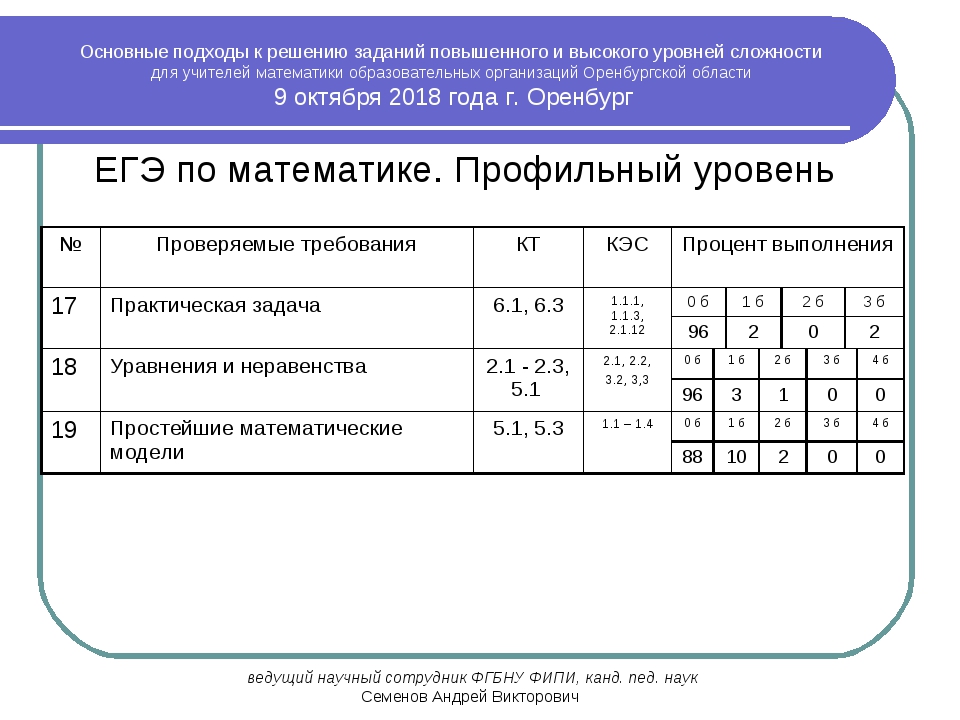
Чем же заменили эти задачи? Мы можем частично ответить на этот вопрос, опираясь на опубликованный демонстрационный вариант, но, согласитесь, одного варианта недостаточно, чтобы составить полное представление о разнообразии новых заданий. Именно поэтому очень важно иметь под рукой пособие, авторами которого являются специалисты, принимающие непосредственное участие в разработке заданий единого государственного экзамена по математике профильного уровня. Такими пособиями, в которых учтены все изменения ЕГЭ по математике, являются сборники издательства «Экзамен» под редакцией И.В.Ященко: «ЕГЭ 2022. Математика. Профильный уровень. 50 вариантов. Типовые варианты экзаменационных заданий от разработчиков ЕГЭ» и «ЕГЭ 2022. Математика. Профильный уровень. 37 вариантов. Типовые варианты экзаменационных заданий от разработчиков ЕГЭ».
Рассмотрим подробнее изменения в структуре КИМов 2022 года. Новыми являются задание 9, проверяющее умение выполнять действия с функциями, и задание 10 (повышенного уровня сложности), проверяющее умение моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий, при этом в первой части работы осталось задание базового уровня сложности, проверяющее те же самые умения. Понятно, что изменилась привычная для учителей математики нумерация заданий и их количество уменьшилось с 19 до 18. Изменения в системе оценивания коснулись второй части работы в заданиях с развернутым ответом. Так, стереометрическая задача 13 оценивается теперь в три первичных балла, экономическая задача 15 – в два балла, а максимальное общее количество баллов за экзаменационную работу снизилось до 31.
Понятно, что изменилась привычная для учителей математики нумерация заданий и их количество уменьшилось с 19 до 18. Изменения в системе оценивания коснулись второй части работы в заданиях с развернутым ответом. Так, стереометрическая задача 13 оценивается теперь в три первичных балла, экономическая задача 15 – в два балла, а максимальное общее количество баллов за экзаменационную работу снизилось до 31.
Обратимся к учебному пособию издательства «Экзамен», где представлено 50 тренировочных вариантов с учетом введенных изменений.
Анализируя представленные в сборнике варианты задания 9, проверяющего умение выполнять действия с функциями, можно сделать вывод о том, что для успешного их выполнения выпускник должен уметь от графического способа задания функции переходить к аналитическому. Приведем пример такого задания.
Вариант 1. Задание №9. На рисунке изображен график функции f(x)=kx+b. Найдите значение х, при котором выполнено f(x) = -13,5.
Понятно, что для выполнения подобных заданий школьникам необходимо вспомнить разделы курса алгебры 7-9-х классов, связанные с элементарными функциями и их графиками. Введение подобного задания в структуру КИМов ЕГЭ по математике мне кажется весьма целесообразным, так как на изучение этой темы выделяется большое количество часов, а в предыдущей версии КИМов профильного экзамена по математике в заданиях с кратким ответом умения выполнять действия с функциями не проверялись.
Введение подобного задания в структуру КИМов ЕГЭ по математике мне кажется весьма целесообразным, так как на изучение этой темы выделяется большое количество часов, а в предыдущей версии КИМов профильного экзамена по математике в заданиях с кратким ответом умения выполнять действия с функциями не проверялись.
В новой версии экзаменационной работы в заданиях с кратким ответом содержится две задачи на тему «Элементы комбинаторики, статистики и теории вероятности». Предлагаю обратить внимание на примеры заданий 10 повышенного уровня сложности на эту тему из сборника «ЕГЭ 2022. Математика. Профильный уровень. 50 вариантов. Типовые варианты экзаменационных заданий от разработчиков ЕГЭ».
Вариант 11. Задание №10. Первый член последовательности целых чисел равен 0. Каждый следующий член последовательности с вероятностью р = 20/33 на единицу больше предыдущего и с вероятностью 1-р на единицу меньше предыдущего. Какова вероятность того, что какой-то член этой последовательности окажется равен -1?
Вариант 26. Задание №10. Первый игральный кубик обычный, а на гранях второго кубика нет чисел, больших, чем 2, а числа 1 и 2 встречаются по три раза. В остальном кубики одинаковые. Один случайно выбранный кубик бросают два раза. Известно, что в каком-то порядке выпало 1 и 2 очка. Какова вероятность того, что бросали второй кубик?
Все описанное выше не входило в прототипы заданий профильного ЕГЭ прошлых лет и является абсолютно новым. Нельзя сказать, что оно будет легким для наших выпускников. Ведь для успешного решения этих задач необходимо внимательно ознакомиться с условием, составить правильную математическую модель и применить знания по нахождению вероятности события в конкретной ситуации. Таким образом, для успешной подготовки школьников к профильному экзамену учителям математики необходимо больше, чем раньше, уделять внимания задачам на тему «Элементы комбинаторики, статистики и теории вероятности».
SAT Math Примеры вопросов | College Board
Указания и номера вопросов ниже отражают то, с чем студенты столкнутся в день экзамена. Некоторые математические разделы позволяют использовать калькулятор, а другие – нет, как указано в инструкциях.
Откройте Раздел 3 своего листа для ответов, чтобы ответить на вопросы этого раздела.
Для вопросов 1–15 решите каждую задачу, выберите лучший ответ из предложенных вариантов и закрасьте соответствующий кружок на листе для ответов.Для вопросов 16–20 решите проблему и введите свой ответ в сетку на листе для ответов. Пожалуйста, ознакомьтесь с инструкциями перед вопросом 16 о том, как ввести свои ответы в сетку. Вы можете использовать любое доступное место в вашем тестовом буклете для черновой работы.
- Использование калькулятора [разрешено] / [запрещено].
- Все используемые переменные и выражения представляют собой действительные числа, если не указано иное.
- Рисунки, представленные в этом тесте, нарисованы в масштабе, если не указано иное.
- Все фигуры лежат на одной плоскости, если не указано иное.
- Если не указано иное, область заданной функции f представляет собой набор всех действительных чисел x , для которых является действительным числом.
Каталожный номер
Число градусов дуги в окружности 360.
Число радианов дуги в окружности
Сумма углов треугольника в градусах равна 180.
Для вопросов, задаваемых студентами, студенты также увидят следующие направления:
Для вопросов 16–20 решите проблему и введите свой ответ в сетку, как описано ниже, на листе ответов.
- Хотя это и не обязательно, рекомендуется написать свой ответ в полях вверху столбцов, чтобы помочь вам правильно заполнить кружки. Вы получите кредит только в том случае, если кружки заполнены правильно.
- Отметьте не более одного кружка в любом столбце.
- Ни один вопрос не имеет отрицательного ответа.
- Для некоторых задач может быть несколько правильных ответов. В таких случаях сетка только один ответ.
- Смешанные числа, например, должны быть разделены на сетку как 3,5 или
(если ввести в сетку как, оно будет интерпретировано как не - Десятичные ответы: если вы получаете десятичный ответ с большим количеством цифр, чем может вместить сетка, он может быть либо округлен, либо усечен, но он должен заполнять всю сетку.
Если вы будете запрашивать (или были одобрены) для размещения формата, совместимого с вспомогательными технологиями (цифровое тестирование для использования с программой чтения с экрана или другой вспомогательной технологией) для SAT, вы можете также просмотреть примеры математических заданий в их полностью отформатированные версии, отсортированные как вопросы, допускающие использование калькулятора, и вопросы, не разрешающие использование калькулятора.
Обратите внимание, что все условия тестирования, в том числе запросы на вспомогательные технологии и специальные форматы, должны быть одобрены Службой Совета колледжей для студентов с ограниченными возможностями до начала экзамена.
SAT Math Test | College Board
Математический тест SAT охватывает ряд математических практик с упором на решение задач, моделирование, стратегическое использование инструментов и алгебраическую структуру.
Важный:Попробуйте примерные вопросы по математике прямо сейчас
Речь идет о реальном мире
Вместо того, чтобы проверять вас по каждой математической теме, SAT просит вас использовать математику, на которую вы будете полагаться больше всего в самых разных ситуациях.Вопросы к тесту по математике предназначены для отражения решения задач и моделирования, которые вы будете выполнять в:
- Курсы математики, естественных и социальных наук в колледже
- Рабочие места, которые у вас есть
- Твоя личная жизнь
Например, чтобы ответить на некоторые вопросы, вам нужно будет выполнить несколько шагов, потому что в реальном мире одного вычисления редко бывает достаточно для выполнения работы.
Краткая информация
- В большинстве математических вопросов будет несколько вариантов ответа, но некоторые, называемые сетками, просят вас придумать ответ, а не выбрать ответ.
- Математический тест разделен на две части: математический тест – калькулятор и математический тест – без калькулятора.
- Некоторые части теста включают несколько вопросов по одному сценарию.
фокус
Тест по математике будет посвящен трем областям математики, которые играют наибольшую роль в широком спектре специальностей и профессий в колледже:
Тест по математике также включает дополнительные разделы математики, в том числе геометрию и тригонометрию, наиболее важные для подготовки к колледжу и карьеры.
Посмотреть видео
Что измеряет математический тест?
Свободное владение
Тест по математике – это шанс показать, что вы:
- Выполняйте процедуры гибко, точно, эффективно и стратегически.
- Быстро решайте проблемы, определяя и используя наиболее эффективные подходы к решению. Это может включать решение проблемы путем проверки, поиска ярлыка или реорганизации предоставленной вам информации.
Концептуальное понимание
Вы продемонстрируете свое понимание математических понятий, операций и отношений. Например, вас могут попросить установить связи между свойствами линейных уравнений, их графиками и контекстами, которые они представляют.
Приложения
Эти реальные проблемы требуют от вас анализа ситуации, определения основных элементов, необходимых для решения проблемы, математического представления проблемы и выполнения решения.
Использование калькулятора
Калькуляторы– важные инструменты, и чтобы добиться успеха после окончания школы, вам нужно знать, как и когда ими пользоваться. В части теста “Тест по математике – калькулятор” вы сможете сосредоточиться на сложном моделировании и рассуждениях, потому что калькулятор поможет вам сэкономить время.
Однако калькулятор, как и любой другой инструмент, настолько умен, насколько умен человек, который его использует. Тест по математике включает несколько вопросов, по которым лучше не использовать калькулятор, даже если вам это разрешено.В этих случаях студенты, которые используют структуру или свою способность рассуждать, вероятно, закончат раньше, чем студенты, использующие калькулятор.
Тест по математике – часть теста без калькулятора облегчает оценку вашего владения математикой и вашего понимания некоторых математических понятий. Он также проверяет хорошо изученную технику и чувство чисел.
Общие вопросы
Хотя большинство вопросов в тесте по математике представляют собой вопросы с несколькими вариантами ответов, 22 процента – это вопросы с ответами учащихся, также известные как сетки.Вместо того, чтобы выбирать правильный ответ из списка вариантов, вам нужно будет решить проблемы и ввести свои ответы в сетки на листе для ответов.
Привязка ответов
- Отметьте не более одного кружка в любом столбце.
- Оцениваются только ответы, отмеченные кружком (вы не получите баллов за все, что написано в полях, расположенных над кружками).
- Неважно, в каком столбце вы начинаете вводить их ответы; пока ответы записываются в области сетки, вы получите кредит.
- Сетка может содержать только четыре десятичных разряда и может содержать только положительные числа и ноль.
- Если проблема не указывает на иное, ответы можно вводить в сетку в виде десятичных или дробных чисел.
- Такие дроби не нужно сокращать до наименьшего значения.
- Все смешанные числа необходимо преобразовать в неправильные дроби перед записью в сетку.
- Если ответ – повторяющаяся десятичная дробь, учащиеся должны нанести на сетку наиболее точное значение, которое она сможет учесть.
Ниже приведен образец инструкций, которые студенты увидят на тесте.
Примеры вопросов
Узнайте о тесте по математике из первых рук, просмотрев образцы вопросов из теста SAT.
Самый полный обзор математической части ТЕСТА FSA: Назари, Реза, Росс, Ава: 9781985268487: Amazon.com: Книги
Единственная книга, которая когда-либо понадобится вашему ученику, чтобы успешно сдать экзамен по математике FSA!
Учебное пособие по математике FSA дает учащимся уверенность и математические навыки, необходимые им для успешной сдачи экзамена FSA Math, обеспечивая прочную основу для основных тем по математике с множеством упражнений по каждой теме.Он разработан, чтобы удовлетворить потребности тестируемых FSA, которые должны иметь практические знания базовой математики.
Эта исчерпывающая рабочая тетрадь с более чем 1500 типовых вопросов и 2 полными 5 тестами FSA -го уровня – это все, что нужно вашему ученику для полной подготовки к FSA Math. Это поможет вашему ученику выучить все, что ему нужно, чтобы преуспеть в математическом разделе FSA.
В этой книге более 1500 математических задач с ответами.
Уникальная учебная программа по математике, не требующая усилий, позволяет вашим ученикам глубоко сосредоточиться на математической части экзамена, помогая им овладеть математическими навыками, которые учащиеся считают наиболее проблемными.
Эта рабочая тетрадь содержит наиболее часто встречающиеся примеры вопросов, которые с наибольшей вероятностью появятся в разделе математики FSA.
На страницах этого всеобъемлющего учебного пособия учащиеся могут изучать основные математические операции в структурированной форме с помощью полной учебной программы, которая поможет им понять основные математические навыки. Он также имеет множество интересных функций, в том числе:
- Динамический дизайн и простые для выполнения упражнения
- Веселый, интерактивный и конкретный процесс обучения
- Целевые практики развития навыков
- Веселые упражнения, укрепляющие уверенность
- Математические темы сгруппированы по категориям, поэтому студенты могут сосредоточиться на проблемных темах
- Включены все решения для упражнений, поэтому вы всегда найдете ответы
- 2 Полные практические тесты по математике FSA, которые отражают формат и типы вопросов в FSA
Простая книга по математике FSA – невероятно полезный инструмент для тех, кто хочет просмотреть все темы, затронутые в тесте FSA.Он эффективно и действенно подкрепляет результаты обучения с помощью интересных вопросов и многократной практики, помогая учащимся быстро овладеть основными математическими навыками.
Издатель:
Простое математическое образование
www.EffortlessMath.com
Анализ скрытого профиля математической тревожности и математической мотивации
Abstract
Математическая тревога (MA) и математическая мотивация (MM) являются важными многомерными некогнитивными факторами в обучении математике.В то время как отрицательная связь между глобальной MA и MM хорошо воспроизводится, отношения между конкретными измерениями MA и MM в значительной степени не исследованы. В настоящем исследовании использовался латентный анализ профиля для изучения профилей различных аспектов магистратуры (включая обучение магистратуре и экзамен на степень магистра) и ММ (включая важность, самовоспринимаемые способности и интерес), чтобы обеспечить более целостное понимание эмоций, связанных с математикой. и мотивационный опыт. В выборке из 927 старшеклассников (13–21 лет) мы обнаружили 8 различных профилей, характеризующихся различными комбинациями измерений МА и ММ, что выявило сложность математически специфических отношений эмоций и мотивации за пределами одной отрицательной корреляции.Кроме того, эти профили различались по поведению при обучении математике и успеваемости по математике. Например, студенты с наивысшей успеваемостью сообщили о скромном экзамене MA и высоком MM, тогда как наиболее заинтересованные студенты характеризовались сочетанием высокого уровня MA на экзамене и высокого MM. Эти результаты требуют выхода за рамки линейных отношений между глобальными конструкциями, чтобы решить сложность взаимодействия эмоций, мотивации и познания в обучении математике, и подчеркнуть важность индивидуального вмешательства для этих разнородных групп.
Образец цитирования: Wang Z, Shakeshaft N, Schofield K, Malanchini M (2018) Беспокойства недостаточно, чтобы меня оттолкнуть: латентный анализ профиля математической тревожности и математической мотивации. PLoS ONE 13 (2): e0192072. https://doi.org/10.1371/journal.pone.0192072
Редактор: Лутц Янке, Цюрихский университет, ШВЕЙЦАРИЯ
Поступила: 23 мая 2017 г .; Одобрена: 16 января 2018 г .; Опубликован: 14 февраля 2018 г.
Авторские права: © 2018 Wang et al.Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии указания автора и источника.
Доступность данных: Данные не могут быть открыты для совместного использования из-за соображений конфиденциальности. Заинтересованные квалифицированные исследователи могут подать заявку на доступ, отправив запрос на участие в исследовании MILES по адресу http://www.projectmiles.com/research.html. Запросы данных можно отправлять в комитет по доступу к данным по адресу [email protected] или через http://www.projectmiles.com/contact-us.html.
Финансирование: Офис вице-президента по исследованиям Техасского технологического университета предоставил финансирование для публикации в открытом доступе для поддержки этой работы. Спонсор не имел никакого отношения к дизайну исследования, сбору и анализу данных, принятию решения о публикации или подготовке рукописи.
Конкурирующие интересы: Авторы заявили об отсутствии конкурирующих интересов.
Введение
Математическая тревога (MA) и математическая мотивация (MM) являются важными многогранными некогнитивными факторами в обучении математике. МА относится к страху и опасениям, испытываемым до или во время занятий, связанных с математикой [1]. ММ отражает степень, в которой люди ценят важность математических способностей, интересуются математической деятельностью и мотивированы на хорошие результаты по математике [2]. Хотя исследования неизменно сообщали об умеренных или умеренных отрицательных корреляциях между МА и ММ [3, 4], их отношения, вероятно, более сложны, чем отрицательная линейная связь.
Ван и его коллеги [5] утверждали, что МА и ММ концептуально связаны, но различны. Они связаны, потому что оба отражают валентность математического опыта: MA фиксирует отрицательную оценку (например, страх и беспокойство), а MM – положительную оценку (например, интерес и вознаграждение). Тем не менее, МА и ММ – это разные конструкции, а не два противоположных конца континуума. MM учитывает аспект мотивации, который определяет подход к математической деятельности, а не ориентацию на отказ от нее, тогда как MA предлагает мало информации в этом отношении.Другими словами, учащиеся, испытывающие опасения по поводу математической деятельности, могут избегать подобных ситуаций в будущем [6], или они могут преодолевать такие эмоциональные проблемы, вкладывая больше усилий [7, 8], причем эти разные ответы, вероятно, связаны с тем, насколько они мотивированы. . Эта концептуализация согласуется с данными факторного анализа, показывающими, что MA и MM представляют собой две отдельные, но умеренно коррелированные конструкции [9, 10]. Такая концептуализация указывает на сложную многомерную взаимосвязь эмоции и мотивации, которая требует дальнейшего исследования.
Кроме того, MA и MM являются многогранными конструкциями. В зависимости от инструментов, используемых для измерения MA, были обнаружены разные факторные структуры. Четыре наиболее распространенных фактора – это беспокойство по поводу математических тестов [11–13], беспокойство по поводу выполнения числовых операций [11–12, 14], беспокойство по поводу выполнения математических задач в социальных ситуациях [12–13] и беспокойство по поводу наблюдения и изучения материалов в математика [3, 15]. Что касается мотивации, три наиболее изученных измерения – это самооценка, интерес и важность [2].Самовоспринимаемая способность измеряет восприятие людьми своей компетентности в различных математических задачах. Интерес указывает на удовольствие, которое человек получает от изучения и выполнения математики. Важность относится к осознанной важности хороших результатов по математике. Учитывая, что обе конструкции многогранны, возможно, что разные аспекты MA и MM по-разному связаны друг с другом. Например, ученики, которые боятся изучать новые материалы по математике, вряд ли получат удовольствие от изучения математики, но они все равно могут считать важным овладение математикой.Студенты, которые чувствуют себя компетентными в своих математических способностях, могут по-прежнему беспокоиться о том, что допустят ошибку на предстоящем экзамене. Следовательно, одной корреляции между глобальной MA и MM кажется недостаточным для фиксации этих сложных многомерных отношений. Чтобы устранить этот пробел, первая цель настоящего исследования – изучить отношения между конкретными измерениями МА и ММ.
Конечная цель изучения эмоций и мотивационных переживаний – понять, как они связаны с обучением математике и достижениями.Многие существующие исследования изучали, как MA и MM связаны с математическими достижениями и учебным поведением. Более высокий MM и более низкий MA были, соответственно, связаны с более высокими достижениями по математике [4, 16–19] и с большей вовлеченностью в связанные с математикой виды деятельности, такие как прохождение большего количества факультативных курсов по математике [4, 6, 20]. Однако на сегодняшний день мало исследований изучали комбинированные роли МА и ММ и возможность их интерактивного и нелинейного воздействия на обучение математике. Одно исследование показало, что после учета MM, MA больше не ассоциируется с намерением выбрать курсы математики [4], предполагая, что избегание математики в первую очередь связано с аспектом мотивации.Два недавних исследования показали, что MM смягчает связь между MA и успеваемостью по математике [5, 7], так что высокий MM смягчает отрицательную связь между MA и успеваемостью по математике. В совокупности эти исследования показали, что понимание сложных отношений между эмоциями, мотивацией и познанием в математике требует изучения различных некогнитивных характеристик в сочетании, а не изолированно. Таким образом, вторая цель настоящего исследования заключалась в изучении различий в успеваемости по математике и избегании обучения математике среди студентов с разными эмоциональными и мотивационными профилями.
Учитывая, что так мало исследований изучали отношения между конкретными измерениями МА и ММ, в настоящем исследовании использовался исследовательский подход с использованием анализа скрытого профиля, чтобы углубить наше понимание эмоций и мотивационного опыта при обучении математике. Скрытый анализ профиля – это более целостный подход, чем подходы, ориентированные на переменные (например, анализ модерации) при изучении многомерных по своей природе отношений, поскольку он позволяет обнаруживать разнородные группы людей со схожими ценностями по множеству представляющих интерес измерений.Различные профили, полученные в результате анализа латентных профилей, представляют собой естественные группы людей в популяции, характеризующиеся отличительными комбинациями различных связанных с математикой эмоциональных и мотивационных переживаний. Подход к анализу скрытого профиля также позволяет исследовать различия в успеваемости и избегании математики среди учащихся с разными эмоциональными и мотивационными профилями. Было бы чрезвычайно сложно изучить, как несколько измерений MA и MM работают вместе в отношении достижения и избегания, используя подход, ориентированный на переменные, особенно если принимать во внимание как линейные, так и криволинейные, а также аддитивные и интерактивные эффекты.Преимущество латентного анализа профиля заключается в том, что он сужает наш акцент на встречающихся в природе комбинациях различных параметров MA и MM в популяции, в отличие от искусственного разделения выборки на произвольные категории. Сравнивая средства достижения и избегания математики в этих профилях, этот подход позволяет нам исследовать, как существующие комбинации профилей MA и MM относятся к математическим достижениям и избеганию, не предполагая линейности и аддитивности в их отношениях.
Методы
Участники
Эта работа является частью исследования Multi-Cohort Investigation and Educational Success (MILES). MILES – это ускоренное лонгитюдное исследование, целью которого является изучение факторов, влияющих на индивидуальные различия в академической успеваемости и психологическом благополучии во время учебы в средней школе в Италии. Были приглашены все ученики из трех случайно выбранных средних школ провинции Милан, и 1020 учащихся приняли участие в первой волне сбора данных в марте 2016 года.После очистки данных и скрининга 927 студентов (437 мужчин, 490 женщин) внесли данные в настоящее исследование. Возраст студентов колебался от 13 до 21 года ( M = 15,87, SD = 1,49).
Процедура
Все ученики были заранее проинформированы о целях и процедурах на конференциях, проведенных в школах командой MILES. Данные были собраны онлайн через веб-сайт MILES (www.projectmiles.com/test) с использованием онлайн-платформы forepsyte.com (www.forepsyte.com). Первая волна сбора данных длилась около 90 минут и включала когнитивные тесты и самооценку.
MILES получил этическое одобрение от Голдсмитского университета Лондона. Комитеты родителей и учителей каждой школы одобрили проект MILES и протокол сбора данных. Утверждение было получено до сбора данных и обновляется каждый год. Каждому студенту был предоставлен онлайн-информационный лист, объясняющий мотивацию проведенного исследования, и он заполнил онлайн-форму согласия на итальянском языке.Каждого студента проинформировали, что участие было добровольным и что они могут выйти из исследования в любое время. Данные будут доступны исследователям по запросу и после заполнения формы сотрудничества в рамках исследования MILES (http://www.projectmiles.com/research.html).
Меры
Все меры были переведены и введены в действие на итальянском языке. Все переведенные меры были опробованы на выборке из 70 учеников из пяти средних школ в провинции Милан до первой волны сбора данных.Факторная структура, распределение конструктов и связи между конструктами были сопоставимы с теми, которые были получены с помощью проверенных показателей, примененных к англоязычным образцам.
Математическая мотивация (ММ).
Были оценены три аспекта ММ. Аспект 1 st был отношением к математике (т. Е. Важностью), который измерялся с помощью 1 пункта, взятого из исследования PISA (Программа ОЭСР по международной оценке студентов, www.pisa.oecd.org).Студентов попросили оценить по 4-балльной шкале, «насколько, по вашему мнению, важно преуспевать в математике» (1 = совсем нет; 4 = очень хорошо). Для простоты сравнения с другими шкалами, значение «Важность» было изменено на шкалу от 1 до 5 с использованием нормализации минимум-максимум. Результаты остались прежними независимо от трансформации.
Аспект мотивации 2 и – это самооценка математических способностей (т. Е. Самовосприятие). Студентов попросили оценить, насколько хорошо, по их мнению, они справляются с конкретными математическими заданиями по 5-балльной шкале (1 = совсем плохо; 5 = очень хорошо) [21].Конкретные способности включали решение числовых и денежных задач, выполнение математических расчетов в уме, умножение и деление. Альфа Кронбаха для этой шкалы составляла 0,77.
Аспектом мотивации было увлечение математикой (т.е. интерес). Студентов попросили оценить, насколько им понравились указанные выше 3 упражнения по 5-балльной шкале (1 = совсем не нравится; 5 = очень нравится) [21]. Альфа Кронбаха для этой шкалы составляла 0,79.
Математическая тревога (MA). МА
измерялась с использованием сокращенной математической шкалы тревожности (AMAS) [22].Учащимся было предложено оценить по 5-балльной шкале, насколько тревожно / нервно они чувствовали себя в некоторых контекстах и занятиях, связанных с математикой (1 = не все; 5 = очень сильно). Анализ главных компонентов с вращением облимина показал четкую двухкомпонентную структуру, при этом два компонента объясняют 46% и 15% общей дисперсии, соответственно. По компоненту 1 st было загружено пять заданий, которые отражали беспокойство по поводу изучения новых математических материалов или слушания объяснений других математических формул (нагрузки варьировались от 0.55 до 0,86). По компоненту 2 и были загружены три задания, отражающие беспокойство по поводу экзаменов по математике (нагрузки варьировались от 0,84 до 0,90). Один объект имел двойную загрузку и был исключен из анализа, чтобы избежать загрязнения между компонентами. Мы обозначили 2 компонента , обучение MA и экзамен MA . Обе субшкалы внутренне соответствовали альфа Кронбаха 0,79 и 0,87 соответственно. Более высокие баллы указывают на более высокую степень магистра.
Достижение по математике.
Студенты сами сообщили свои оценки по математике за семестр, который закончился в январе, до волны сбора в феврале-марте 2016 года. максимально возможный балл), где 6 означает проходной балл.
Время по математике.
Учащимся было предложено оценить, сколько времени они потратили на «Уроки математики вне школы» и «Саму домашнее задание по математике» по 5-балльной шкале (1 = нет времени; 2 = менее 2 часов; 3 = от 2 до 4 часов; 4 = от 4 до 6 часов; 5 = 6 или более часов; Программа ОЭСР по международной оценке студентов, www.pisa.oecd.org). Эти два элемента были умеренно коррелированы ( r = 0,32) и были усреднены для получения единой оценки, отражающей время, потраченное на математику после школы. Более высокий балл означает больше времени, потраченного на изучение математики после школы, и меньшее избегание.
Аналитические стратегии
Все анализы проводились в SPSS версии 24 [23] и Mplus версии 7.4 [24]. Сначала был проведен описательный и корреляционный анализ, чтобы понять основные свойства переменных.Затем был проведен латентный анализ профиля (LPA) многомерных аспектов MM и MA: математической важности, самооценки математических способностей, интересов к математике, обучения MA и экзамена MA. Лучшая модель была выбрана с использованием байесовского информационного критерия (BIC) [25] в качестве основного критерия и теста отношения правдоподобия Ло-Менделла-Рубина (LMRT) [26] в качестве дополнительного критерия, чтобы установить количество классов и изучить отличительные особенности этих классов. Затем с помощью команды r3step в Mplus мы проверили, предопределяют ли принадлежность к классу по полу и классу.Впоследствии мы проверили, различались ли ученики в разных классах по успеваемости и математическому времени, используя ANOVA.
Результаты
Описательный и корреляционный анализ
Описательная статистика представлена в таблице 1. Все переменные были широко распределены по всей шкале. Среднее значение было ниже для обучения MA по сравнению с экзаменом MA, что позволяет предположить, что экзамен MA был более распространенным по сравнению с изучением MA.
Корреляции показаны в таблице 2.Студентки сообщили о более высоком уровне MA и более низком уровне MM по сравнению со студентами-мужчинами. Уровни успеваемости были слабо связаны с важностью, что свидетельствует о том, что учащиеся старших классов склонны рассматривать математику как менее важную. Экзамен MA и обучение MA были умеренно положительно коррелированы, как и различные аспекты MM. И экзамен MA, и обучение MA были умеренно отрицательно коррелированы с различными аспектами MM. Успехи по математике были связаны умеренно отрицательно с MA и умеренно положительно с MM.Время на математику было положительно связано с экзаменом MA, важностью и интересом. Наконец, время, проведенное по математике, было умеренно негативно связано с математическими достижениями.
Анализ скрытого профиля
Анализ скрытых профилей был проведен для изучения профилей MA и MM. Были запущены девять моделей от 2 до 10 классов, и лучшая модель была выбрана с помощью BIC и LMRT. Как показано в Таблице 3, BIC уменьшался по мере увеличения количества классов, но снижение стало минимальным, начиная с 7-го класса до 8-го класса.Согласно LMRT, модель 8 классов была лучше, чем модель 7 классов, тогда как модель 9 классов не лучше, чем модель 8 классов. Поэтому лучшей была выбрана модель 8-го класса.
На рис. 1 и в таблице 4 показаны характеристики каждого из 8 классов. Из-за большого количества классов здесь мы сначала описываем правила, которые мы использовали для упорядочивания и маркировки 8 классов: Как показано на рисунке 1, при рассмотрении уровней MM 8 классов сгруппированы в 3 группы: первая группа включала 2 класса, которые показал высокий ММ, во вторую группу вошли 3 класса, показывающие средний ММ, а в третью группу вошли еще 3 класса, показывающие низкий ММ.Это наблюдалось по всем трем параметрам ММ (важность, самовосприятие и интерес). Поэтому сначала мы упорядочили классы в соответствии с уровнями MM и обозначили группы 1 st , 2 и и 3 rd соответственно как «высокий MM» (классы 1-2), «средний MM» (классы 3–5) и группы «низкого ММ» (6–8 классы). В каждой группе ММ классы дополнительно различались по уровням экзамена MA и обучения MA. Поэтому внутри каждой группы MM мы дополнительно упорядочили классы в соответствии с их уровнями MA, чтобы класс, показывающий сравнительно более низкую MA, появился раньше в последовательности.Например, в группе с высоким уровнем MM один класс показал низкий уровень обучения MA и низкий экзамен MA, а другой класс показал низкий уровень обучения и высокий уровень MA на экзамене. Эти два класса были соответственно помечены как класс 1 и класс 2, причем класс 1 показывает более низкий MA по сравнению с классом 2. В следующем разделе, чтобы сократить длинную метку для каждого класса, мы используем H, M и L для представления высокого , средний и низкий уровни, и используйте MM, EMA и LMA для обозначения математической мотивации, беспокойства по поводу экзамена по математике и беспокойства при изучении математики.
Рис. 1. Анализ скрытого профиля: результаты 8-классной модели.
Средние значения в разных эллипсах значительно отличаются друг от друга при заранее заданной частоте ошибок типа I 0,05 после коррекции Бонферрони.
https://doi.org/10.1371/journal.pone.0192072.g001
Высшие классы ММ.
Класс 1 (H MM, L LMA, L EMA): Примерно 13% выборки относились к классу 1 (n = 117). Этот класс показал самый высокий MM и самый низкий уровень обучения MA и экзамен MA среди всех 8 классов.
Класс 2 (H MM, L LMA, H EMA): 19% выборки относились к классу 2 (n = 178). Учащиеся этого класса сообщили об очень высоком уровне MM, очень низком уровне знаний MA, но о высоком экзамене MA.
Сходство между Классом 1 и Классом 2 состояло в том, что они оба показали высокий MM. Эти два класса различались по степени озабоченности по поводу математики. В частности, учащиеся 2-го класса, но не 1-го, сообщали о высокой тревоге по поводу экзаменов по математике.
Средние классы ММ.
Класс 3 (M MM, L LMA, L EMA): 13% выборки были отнесены к классу 3 (n = 122).Этот класс сообщил о среднем уровне MM и низком уровне как обучения MA, так и экзамена MA. Этот класс был похож на Класс 1 в том, что оба класса сообщили об относительно низком МА по сравнению со всеми другими классами. Этот класс отличался от класса 1 тем, что они сообщили о более низком ММ по сравнению с классом 1.
Класс 4 (M MM, L LMA, H EMA): около 26% учеников принадлежали к классу 4 (n = 238), что делает этот класс самым большим. Студенты этого класса имели средний уровень ММ, низкий уровень магистра и высокий экзамен на степень магистра.Как и во 2-м классе, ученики 4-го класса также беспокоились в основном о экзаменах по математике, но не об изучении математики. Однако учащиеся 4-го класса сообщили о более низком ММ по сравнению с учащимися 2-го класса, что кардинально отличает эти два класса.
Класс 5 (M MM, M LMA, H EMA): около 13% студентов были отнесены к этому классу (n = 122). Этот класс характеризовался средним уровнем подготовки к экзамену, средним уровнем магистра и высоким экзаменом на степень магистра.
Эти три класса были похожи тем, что все они демонстрировали средний уровень ММ.Тем не менее, три класса критически различались по уровням экзамена MA и обучения MA, при этом класс 3 имеет низкий уровень как для обучения MA, так и для экзамена MA, класс 4 имеет низкий уровень обучения MA, но высокий по экзамену MA, а класс 5 является средним по изучению MA. и высокие оценки на экзамене MA.
Низкие классы ММ.
Класс 6 (L MM, L LMA, H EMA): 5% выборки относились к классу 6 (n = 48). Учащиеся этого класса сообщили о низком уровне MM, низком уровне успеваемости и высшем экзамене MA. Уровни МА в этом классе напоминали уровни, наблюдаемые в Классе 2 и Классе 4.Что отличает класс 6 от классов 2 и 4, так это более низкий MM по сравнению с двумя другими классами.
Класс 7 (L MM, M LMA, H EMA): около 7% всех учащихся были в классе 7 (n = 68). Этот класс характеризовался низким уровнем MM, средним уровнем MA и высоким экзаменом MA. Этот класс был похож на класс 5, так что оба класса дали высокий экзамен MA и средний уровень MA. Однако у учащихся 7-го класса ММ был ниже, чем у учащихся 5-го класса.
Класс 8 (L MM, H LMA, H EMA): примерно 4% выборки были отнесены к последнему классу (n = 34), что делает его самым маленьким классом.Этот класс показал очень низкий MM и очень высокий уровень как обучения MA, так и экзамена MA.
Class 6, Class 7 и Class 8 были похожи тем, что все три класса демонстрировали низкий уровень MM и высокий уровень экзамена MA. Тем не менее, все три класса различались по уровню обучения MA: 6-й класс – низкий, 7-й – средний, 8-й – высокий.
В таблице 5 приведены основные характеристики каждого класса. При наблюдении за 8 классами возникло несколько интересных закономерностей: 1) высокий экзамен MA появлялся в сочетании с каждым уровнем MM; 2) средняя обучаемость MA появилась в сочетании только с средним и низким MM, но не с высоким MM; 3) МА с высоким уровнем обучения появилась в сочетании только с низким ММ, но не со средним или высоким ММ.
Уровень успеваемости и пол были исследованы как предикторы членства в классе. Результаты показаны в таблице 6. Все эффекты были получены после учета школьных различий. В целом уровень класса не был значимым предиктором принадлежности к классу. Пол в значительной степени предсказывал членство в классах, так что студентки с большей вероятностью принадлежали к классам, характеризующимся сочетанием более низкого MM и более высокого MA по сравнению со студентами-мужчинами.
Взаимосвязь между членством в классе и успеваемостью по математике / время
Мы проверили, было ли членство в классе связано с математическими достижениями и математическим временем, используя ANOVA.Фиктивные переменные, представляющие школы, были введены в модели как ковариаты для контроля школьных различий.
Связь между членством в классе и математическими достижениями.
Членство в классе было существенно связано с математическими достижениями, F (7, 917) = 20,00, p = 0,000, η 2 = 0,12. Результаты апостериорных контрастов показаны на левой панели на рис. 2. Класс 1 показал значительно лучшие результаты по сравнению со всеми семью оставшимися классами.Класс 2 и класс 3 показали схожие результаты, которые были лучше, чем у классов с 4 по 8, но хуже, чем у класса 1. Наконец, не было обнаружено значительных различий в успеваемости по математике между классами с 4 по 8.
Рис. 2. Связь между членством в классе и успеваемостью по математике / математическим временем.
L = низкий, M = средний, H = высокий, MM = математическая мотивация, EMA = тревожность на экзамене по математике, LMA = тревога при изучении математики. Классы существенно не отличаются друг от друга, если их метки содержат одинаковые буквы; классы существенно отличаются друг от друга, если их метки не содержат одинаковых букв.Статистическая значимость рассчитывается при заранее заданной частоте ошибок типа I 0,05 после поправки Холма-Бонферрони.
https://doi.org/10.1371/journal.pone.0192072.g002
Связь между членством в классе и математикой.
Членство в классе также значимо связано с математическим временем, F (7, 917) = 6,27, p = 0,000, η 2 = 0,04. Результаты апостериорных контрастов показаны на правой панели на рис.2.Классы 2, 5 и 8 проводили больше всего времени, тогда как классы 1 и 3 уделяли меньше всего времени изучению математики после школы. Стоит отметить, что класс 2, класс 5 и класс 8 были классами с наивысшим общим MA в каждой группе MM, и они также были классами, которые сообщили, что тратили больше всего времени на внешкольное обучение математике. Напротив, Класс 1 и Класс 3 были классами с самым низким общим MA в каждой группе MM, и они также были классами, которые сообщили, что тратили наименьшее количество времени на внеклассное изучение математики.
Исследование модели развития
Наконец, учитывая, что текущая выборка включает учащихся из разных классов (с 1 по 5 год средней школы), мы также исследовали, были ли различия между классами в успеваемости по математике и времени, затрачиваемом на математику, в разных классах. В таблице 7 представлен размер выборки для каждого класса по комбинациям классов. Учитывая, что нынешний дизайн был поперечным, этот набор анализов был ограничен описанием и визуализацией паттернов.На рис. 3 представлены средние результаты по математике (левая панель) и время математики (правая панель) в каждом классе по классам.
Рис. 3. Связь между членством в классе и успеваемостью по математике / временем обучения по классам.
C = класс; L = низкий, M = средний, H = высокий, MM = математическая мотивация, EMA = тревожность на экзамене по математике, LMA = тревога при изучении математики.
https://doi.org/10.1371/journal.pone.0192072.g003
Различия в успеваемости по математике среди классов.
Сравнение классов в каждой группе MM позволило нам изучить различия в успеваемости, связанные с различиями в MA.В группах с высоким и средним MM классы с более низким EMA, как правило, имели лучшую производительность (т. Е. Сравнение класса 1 с классом 2 и сравнение класса 3 с классом 4 и классом 5). Казалось, что есть небольшие различия в успеваемости, связанные с различиями в обучении магистратуре. Кроме того, различия между Классом 1 и Классом 2 казались больше в более высоких оценках, тогда как различия между Классом 3 и Классом 4 / Классом 5 казались меньше в более высоких оценках, предполагая, что отрицательная связь между EMA и успеваемостью по математике может быть сильнее у высокомотивированных студенты.Модель ассоциации между MA и достижениями была менее четкой в группе с низким MM, возможно, из-за небольшого размера выборки в этих классах.
Разница в продолжительности занятий по математике.
Подобно модели с агрегированными оценками, класс 1 и класс 3, два класса с самым низким общим показателем MA в своих соответствующих группах MM постоянно сообщали об относительно небольшом количестве времени, затрачиваемого на изучение математики после школы. Напротив, класс 2 и класс 5, два класса с наивысшим общим показателем MA в своих соответствующих группах MM, постоянно тратили относительно больше времени на изучение математики после школы по сравнению со всеми другими классами.Все вместе они предполагают, что именно сочетание высокого уровня MM и высокого MA побуждает студентов больше работать над математикой после уроков.
Обсуждение
Разнообразный спектр эмоций и мотиваций, возникающих в процессе обучения математике, имеет огромное значение для математического образования, поскольку они влияют не только на мобилизацию когнитивных ресурсов во время теста по математике, но и на долгосрочное поведение в процессе обучения [6, 27 –28]. Целью настоящего исследования было изучить различные профили многомерных факторов эмоций и мотивации и, в конечном итоге, изучить, как эти факторы взаимодействуют и связаны с практикой обучения математике и достижениями.
Всегда ли студенты, сильно озабоченные математикой, не имеют мотивации в математике?
Используя анализ скрытого профиля, мы обнаружили 8 различных классов, охватывающих различные комбинации MA и MM. Далее мы сгруппировали эти 8 классов в группы с высоким, средним и низким MM, чтобы облегчить понимание характеристик каждого класса и сравнения между классами. Вопреки нынешнему представлению в существующей литературе о том, что у тревожных по математике студентов обычно низкая мотивация [6, 27], наш анализ показывает, что некоторые тревожные по математике учащиеся обладают высокой мотивацией.В частности, учащиеся 2-го класса обладают высокой мотивацией и также отметили высокие экзамены на степень магистра. Класс 4 и 5 показал средний или высокий уровень MM, несмотря на высокий уровень экзамена MA. Таким образом, высокий экзамен MA, кажется, присутствует у студентов с любым уровнем мотивации.
Что касается обучения MA, то MA со средним уровнем обучения наблюдалась только в группах со средним и низким, но не с высоким уровнем MM, а MA с высоким уровнем обучения наблюдалась только в группах с низким MM, но не в группах со средним или высоким MM, что позволяет предположить, что MA с более высоким уровнем обучения обычно связано с более низким ММ.Таким образом, высокомотивированные студенты по-прежнему могут сдавать экзамен на степень магистра, но с меньшей вероятностью будут получать степень магистра. Неудивительно, что учащиеся, испытывающие неловкость на уроках математики, не получают удовольствия от своего опыта, и это согласуется с наблюдением, что высокая степень магистра успеваемости наблюдалась только в сочетании с низкой ММ. Однако беспокойство по поводу предстоящего экзамена по математике может отражать неуверенность учащихся в своих математических способностях или может отражать их стремление к более высоким достижениям, и это согласуется с наблюдением, что высокий экзамен MA наблюдался на всех уровнях ММ.Эти данные указывают на неоднородный характер отношений между различными аспектами МА и ММ [8].
Принадлежность к классам различалась между полами, так что женщины с большей вероятностью принадлежали к классам, характеризующимся сочетанием более низкой MM и более высокой MA по сравнению с мужчинами. Это согласуется с существующей литературой по половым различиям в математических эмоциях и мотивации [6, 29–30].
Как размеры MM и MA соотносятся с математическими достижениями?
В целом, наивысшее достижение получил класс 1, за ним следуют классы 2 и 3.Остальные пять классов показали аналогичные достижения, которые были ниже, чем у первых трех классов. Общая картина предполагает, что комбинация более высокого MM и более низкого MA связана с более высокими достижениями, открытие согласуется с исследованиями, в которых изучалось влияние MA и MM по отдельности [4, 17, 19]. Однако этот результат кажется несовместимым с предыдущим исследованием, показывающим, что учащиеся с сочетанием высокого ММ и среднего МА имели наивысшие математические достижения [5]. Это различие в результатах может быть связано с несколькими факторами.Во-первых, характеристики выборки между двумя исследованиями различаются: в текущем исследовании использовалась выборка старшеклассников из Италии, тогда как в предыдущем исследовании использовались выборки американских учащихся средних школ и колледжей. Во-вторых, в то время как предыдущее исследование было сосредоточено на взаимодействии между глобальной MA и глобальным MM, настоящее исследование сосредоточено на изучении конкретных измерений MA и MM. В-третьих, два исследования критически различаются по способам измерения мотивации. Настоящее исследование сфокусировано на аспектах мотивации, которые широко изучались в литературе, включая воспринимаемую важность математики, самооценку математических способностей и интерес к математике.В предыдущем исследовании мотивация измерялась более широко, включая такие параметры, как сосредоточенное внимание. Наконец, для оценки успеваемости по математике использовались различные меры. Предыдущее исследование основывалось на лабораторных задачах, тогда как в настоящем исследовании использовался экзамен с высокими ставками. Возможно, что связь между умеренными уровнями MA и успеваемостью по математике в дальнейшем зависит от характера математической задачи (т.е. от того, является ли задача высокой или нет) [27]. В будущих исследованиях следует выяснить, какие из вышеперечисленных различий способствовали расхождению результатов между этими двумя исследованиями.
Когда классы были далее разбиты на разные уровни, возникли определенные модели взаимодействия. В частности, при сравнении классов в каждой из групп с высоким и средним ММ (т. Е. Класс 1 против 2 и класс 3 против 4), классы с более высоким MA на экзамене имели более низкие математические достижения. Кроме того, различия между классами 1 и 2 оказались больше, тогда как различия между классами 3 и 4 оказались меньше на более высоких уровнях обучения. Это указывает на то, что высокий уровень MA на экзамене отрицательно связан с успеваемостью по математике у людей с более высоким ММ, и такие эффекты, по-видимому, сильнее в старших классах.Этот результат перекликается с недавним исследованием изучения математики, которое показало, что более высокий уровень стресса во время обучения предсказывает большее забвение содержания курса и отказ от размышлений о курсе только у студентов с сильной математической самооценкой (т. Е. Студентов, которые считают, что они хорошо разбираются в математике). и что для них важно хорошо разбираться в математике), но не тем, у кого слабая математическая самооценка [31]. Оба набора результатов подтверждают версию об угрозе идентичности, в которой утверждается, что стресс и тревога, связанные с конкретной областью, сильнее влияют на людей, которые мотивированы и идентифицируют себя с этой конкретной областью.
В группе с низким уровнем MM, похоже, нет четкой связи между экзаменом MA и успеваемостью по математике. Вполне возможно, что низкий уровень MA на экзамене не влияет на отрицательную связь между низким уровнем MM и плохой успеваемостью по математике. Также возможно, что мы не смогли наблюдать какой-либо систематической закономерности из-за небольшого размера выборки в группе с низким ММ. Наконец, казалось, что есть небольшие различия в успеваемости по математике, связанные с различиями в обучении магистратуре.
Как размеры ММ и МА связаны с отказом от математики?
Вопреки существующему мнению, что очень тревожные ученики избегают математики [6, 27], наши результаты показали, что в каждой группе ММ более тревожные ученики, как правило, были более вовлечены на всех уровнях обучения.В сочетании с высокой мотивацией беспокойство по поводу математики приводит к увеличению усилий и инвестиций в изучение математики, а не к большему избеганию. Расхождение между настоящим открытием и предыдущей литературой может быть связано с различием в практическом применении математического избегания. Большинство исследований на сегодняшний день сосредоточено на избегающем поведении в отдаленных ситуациях, когда студенты имеют больше свободы выбора между альтернативами [27], например, выбирать или нет факультативный курс математики или делать в будущем карьеру, связанную с математикой.В настоящем исследовании мы изучили, сколько времени старшеклассники тратили на изучение математики после школы, принимая внеклассные уроки математики и самостоятельно изучая математику как часть своего домашнего задания. Эти упражнения представляют собой поведение избегания математики в неизбежных учебных ситуациях в старшей школе, когда непосредственные негативные последствия возникают из-за плохой успеваемости на обязательных курсах математики (например, низкий средний балл отрицательно влияет на поступление в колледж).
Предыдущая литература по реагированию на угрозу предполагает, что угроза может вызывать как ориентированные на приближение, так и ориентированные на отход, ответы в зависимости от характеристик угрожающей ситуации.Ускользающая угроза на большом расстоянии с большей вероятностью вызывает поведение отстранения / избегания, тогда как неизбежная угроза на близком расстоянии с большей вероятностью вызывает реакции, ориентированные на приближение [32]. Таким образом, возможно, что студенты с высоким уровнем магистратуры полагаются на разные стратегии, чтобы справиться со своими негативными эмоциями в разных учебных ситуациях: они вкладывают больше усилий в изучение математики, чтобы избежать немедленных негативных последствий, связанных с плохой успеваемостью по математике, но они предпочитают отказаться от математики. обучение, когда оно не дает немедленного отрицательного результата.
Стоит отметить, что в каждой группе MM, хотя классы с более высоким MA сообщали о большем количестве учебных усилий, они, как правило, имели более низкие достижения по сравнению с классами с более низким MA. Другими словами, в рамках каждого уровня ММ студенты старших курсов магистратуры работали дольше, но хуже успевали по математике. Два возможных механизма могут объяснить это нелогичное открытие. Предыдущие исследования показали, что МА снижает успеваемость по математике из-за снижения эффективности рабочей памяти [16], когнитивной способности, которая играет важную роль как в успеваемости по математике, так и в обучении математике [33–34].Для студентов, которые на экзамене отметили степень магистра, но не учились (например, 2-й класс), степень магистра может повлиять только на успеваемость на экзаменах по математике с высокими ставками [27], но не на получение знаний на уроках математики. Следовательно, высокие ставки на экзамене могут не отражать истинные математические способности учащихся с высокими экзаменами MA [27]. Поскольку студенты с высокими экзаменами MA постоянно тратят дополнительные усилия на изучение математики, возможно, что они усвоят больше знаний, чем то, что отражается в их результатах экзамена, но такие знания могут быть получены только с помощью альтернативных оценок с низким уровнем стресса, таких как бессрочное тестирование.Однако механизм может быть другим для студентов, которые страдают от обучения в магистратуре. Для этих студентов нарушения в познании математики могут быть более серьезными, поскольку степень магистра может также препятствовать процессу приобретения знаний на ежедневных уроках математики. Таким образом, этим учащимся, возможно, придется учиться дольше, чем их сверстникам, чтобы выполнить такой же объем работы, из-за их более слабых математических способностей.
Настоящее исследование имеет некоторые ограничения. Во-первых, все основные конструкции были самоотчетами. В результате отношения между переменными могли быть завышены из-за артефакта метода.Для проверки воспроизводимости и обобщаемости текущих результатов необходим дизайн с множеством информаторов и множеством методов. Во-вторых, две шкалы (важность и время по математике) содержали слишком мало элементов, чтобы оценить их внутреннюю надежность. Однако их корреляции с другими переменными соответствовали существующей литературе, предоставляя доказательства, подтверждающие их прогностическую ценность. Наконец, из-за дизайна поперечного сечения мы не смогли статистически изучить, как различия между восемью классами менялись с течением времени.Будущие продольные данные проекта MILES позволят нам лучше понять траектории развития этих разнообразных профилей.
Таким образом, в настоящем исследовании изучались профили математических эмоций и мотиваций в подростковом возрасте. Наши результаты показали, что взаимосвязь между MA и MM и их совместными ролями в математических достижениях и избегании математики сложна. Эти разнообразные профили требуют индивидуального вмешательства для устранения разнородных механизмов, лежащих в основе низкой успеваемости по математике.Некоторым учащимся может быть достаточно выяснить, как тревога влияет на обработку когнитивных функций в Интернете во время сложных экзаменов по математике, чтобы убедиться, что учебная оценка отражает их истинные способности. Для других учеников более актуальным является вопрос о том, как тревога влияет на процессы внимания и памяти, которые необходимы для оптимального обучения на ежедневных уроках математики. Наконец, для наименее мотивированных студентов приоритетной задачей может быть формирование внутреннего стремления к математике.
Благодарности
Мы благодарим всех студентов и преподавателей Istituto Tecnico S.Канниццаро, Технологический институт Э. Маттери, Лисео К. Ребора и Лисео Сайентико Э. Майорана в городе Ро (Милан). Мы особенно благодарны Елене Бардуччи, Рите Лоффредо, Нади Болдрин и Козимо Морроне за их постоянную поддержку проекта MILES. Мы также хотели бы поблагодарить офис вице-президента по исследованиям Техасского технологического университета за предоставление финансирования публикаций в открытом доступе для поддержки этой работы.
Список литературы
- 1. Суинн Р.М., Уинстон Э.Шкала оценки тревожности по математике, краткая версия: Психометрические данные. Psychol Rep. 2003; 92: 167–173. pmid: 12674278
- 2. Wigfield A, Eccles JS. Ожидательно-ценностная теория мотивации достижения. Contemp Educ Psychol. 2000; 25 (1): 68–81. pmid: 10620382
- 3. Чиу Л.Х., Генри Л.Л. Разработка и проверка математической шкалы тревожности для детей. Meas Eval Couns Dev. 1990; 23 (3): 121–127.
- 4. Мис Дж. Л., Вигфилд А., Экклс Дж. С..Предикторы математической тревожности и ее влияние на намерения подростков поступить на курсы и их успеваемость по математике. J Educ Psychol. 1990; 82 (1): 60–70.
- 5. Ван З., Луковски С.Л., Харт С.А., Лайонс И.М., Томпсон Л.А., Ковас Й. и др. Всегда ли беспокойство по поводу математики плохо сказывается на изучении математики? Роль математической мотивации. Psychol Sci. 2015; 26 (12): 1863–1876. pmid: 26518438
- 6. Хембри Р. Природа, эффекты и облегчение математической тревоги. J Res Math Educ.1990; 21 (1): 33–46.
- 7. Лайонс I, Бейлок С. Математическая тревога: отделить математику от тревоги. Cereb Cortex. 2012; 22: 2102–2110. pmid: 22016480
- 8. Вигфилд А., Мис Дж. Л. Тревога по математике у учеников начальной и средней школы. J Educ Psychol. 1988; 80: 210–216.
- 9. Бай Х, Ван Л., Пан В., Фрей М. Измерение тревожности математики: Психометрический анализ двумерной аффективной шкалы. J Instruct Psychol. 2009; 36: 185–193.
- 10. Krinzinger H, Kaufmann L, Willmes K. Математическая тревожность и математические способности в первые годы начальной школы. J Psychoeduc Assess. 2009; 27: 206–225. pmid: 20401159
- 11. Гопко ДР. Подтверждающий факторный анализ математической рейтинговой шкалы тревожности – переработка. Educ Psychol Meas. 2003; 63: 336–351.
- 12. Луковски С.Л., Дитрапани Дж.Б., Чон М., Ван З., Шенкер В.Дж., Доран М.М. и др. Многомерность измерения математической тревожности и ее связи с математическими навыками.Изучите индивидуальные различия. 2016; Скоро.
- 13. Суинн Р.М., Тейлор С., Эдвардс Р.В. Шкала оценки тревожности математиков Суинна для учащихся начальной школы (MARS-E): психометрические и нормативные данные. Educ Psychol Meas. 1988; 48 (4): 979–986.
- 14. Gierl MJ, Bisanz J. Беспокойство и отношение к математике в 3 и 6 классах. J Exp Educ. 1995; 63 (2): 139–158.
- 15. Bessant KC. Факторы, связанные с типами математической тревожности у студентов колледжей.J Res Math Educ. 1995; 26 (4): 327–345.
- 16. Ashcraft MH, Krause JA. Рабочая память, успеваемость по математике и беспокойство по поводу математики. Psychon Bull Rev.2007; 14 (2): 243–248. pmid: 17694908
- 17. Луо Ю.Л., Ковас И., Хаворт К.М., Пломин Р. Этиология математической самооценки и математических достижений: понимание отношений с помощью перекрестного исследования близнецов в возрасте от 9 до 12 лет. Изучите индивидуальные различия. 2011; 21 (6): 710–718. pmid: 22102781
- 18.Миддлтон Дж. А, Испания, Пенсильвания. Мотивация к достижениям в математике: выводы, обобщения и критика исследования. J Res Math Educ. 1999; 30 (1): 65–68.
- 19. Рамирес Г., Гундерсон Е.А., Левин СК, Бейлок С.Л. Тревога по математике, рабочая память и математические достижения в начальной школе. J Cogn Dev. 2013; 14 (2): 187–202.
- 20. Симпкинс С.Д., Дэвис-Кин ЧП, Экклс Дж. С.. Мотивация к математике и естествознанию: продольное изучение связей между выбором и убеждениями.Dev Psychol. 2006; 42 (1): 70–83. pmid: 16420119
- 21. Спинат Б, Спинат FM, Харлаар Н., Пломин Р. Прогнозирование успеваемости в школе на основе общих когнитивных способностей, самооценки и внутренней ценности. Интеллект. 2006; 34 (4): 363–374.
- 22. Хопко Д.Р., Махадеван Р., Голый Р.Л., Охота МК. Сокращенная математическая шкала тревожности (AMAS): построение, валидность и надежность. Оценка. 2003; 10 (2): 178–182. pmid: 12801189
- 23. IBM Corp.IBM SPSS Statistics для Windows, версия 24.0. Нью-Йорк: IBM Corp. Выпущено в 2016 году.
- 24. Muthén LK, Muthén BO. Руководство пользователя Mplus (7 -е издание ). Лос-Анджелес: Muthén & Muthén; 1998–2015 гг.
- 25. Шварц Г. Оценка размерности модели. Ann Stat. 1978; 6 (2): 461–464.
- 26. Lo Y, Mendell N, Rubin D. Проверка количества компонентов в нормальной смеси. Биометрика. 2001; 88: 767–778.
- 27. Эшкрафт MH, Мур AM.Тревога по математике и аффективное падение успеваемости. J Psychoeduc Assess. 2009; 27 (3): 197–205.
- 28. Мэлони Э.А., Шеффер М.В., Бейлок С.Л. Математическая тревога и угроза стереотипов: общие механизмы, негативные последствия и многообещающие вмешательства. Res Math Educ. 2013; 15 (2): 115–128.
- 29. Дивайн А., Фосетт К., Сзукс Д., Даукер А. Гендерные различия в математической тревожности и связь с успеваемостью по математике при контроле тестовой тревожности.Behav Brain Funct. 2012; 8 (1): 33.
- 30. Прекель Ф., Гетц Т., Пекрун Р., Кляйн М. Гендерные различия у одаренных учеников и учащихся со средними способностями: сравнение достижений, самооценки, интереса и мотивации девочек и мальчиков в математике. Подарок ребенку Q. 2008; 52 (2): 146–159.
- 31. Рамирес Дж., Макдонау И.М., Джин Л. Стресс в классе способствует мотивированному забыванию математических знаний. J Educ Psychol. 2017; 109 (6): 812–825.
- 32. Бланшар, округ Колумбия, Хайнд А.Л., Минке К.А., Минемото Т., Бланшар Р.Дж.Защитное поведение человека по отношению к сценариям угроз показывает параллели с защитными паттернами, связанными со страхом и тревогой, у млекопитающих, кроме человека. Neurosci Biobehav Rev.2001; 25: 761–770. pmid: 11801300
- 33. Алловай ТП. Как рабочая память работает в классе? Educ Res Rev.2006; 1 (4): 134–139.
- 34. Рагхубар К.П., Барнс М.А., Хехт С.А. Рабочая память и математика: обзор развития, индивидуальных различий и когнитивных подходов. Изучите индивидуальные различия.2010; 20 (2): 110–122.
Тест ACT Практические вопросы по математике
Тест ACT по математике Вопросы для практических тестов | ДЕЙСТВОВАТЬ перейти к содержаниюact.org, actprofile.org, act.org, actstudent.org, act.alertline.com, services.actstudent.org, Care4.successfactors.com, Engagement.act.org, discoveractaspire.org, qc.vantage.com , myworkkeys.act.org, twitter.com, facebook.com, youtube.com, plus.google.com, linkedin.com, preview.act.org, workreadycommunities.org, pearson.com, instagram.com, actaspire.org, run2.careerready101.com, run2.keytrain.com, лидерствоblog.act.org
Тестовые подсказки
Настоящий тест по математике ACT содержит 60 вопросов, на которые нужно ответить за 60 минут.
- Внимательно прочтите каждый вопрос, чтобы убедиться, что вы понимаете тип требуемого ответа.
- Если вы решите использовать калькулятор, убедитесь, что он разрешен, работает в день проверки и имеет надежные батареи.
- Используйте свой калькулятор с умом.
- Решите проблему.
- Найдите ваше решение среди вариантов ответа.
- Убедитесь, что вы ответили на заданный вопрос.
- Убедитесь, что ваш ответ разумный.
- Проверьте свою работу.
Наконечники калькулятора
- Просмотрите последнюю информацию о разрешенных и запрещенных калькуляторах.
- Вы не обязаны использовать калькулятор. Все проблемы решаются без калькулятора.
- Если вы регулярно используете калькулятор в своей математической работе, воспользуйтесь уже знакомым вам калькулятором при прохождении теста по математике. Использование более мощного, но незнакомого калькулятора вряд ли даст вам преимущество перед обычным калькулятором.
Щелкните по выбранным буквам ниже, чтобы просмотреть правильный ответ и пояснения.
Для полного взаимодействия с Практикой просмотрите эту страницу на планшете или настольном устройстве.
НАПРАВЛЕНИЯ: Решите каждую задачу, выберите правильный ответ, а затем закрасьте соответствующий овал в своем ответе.
Не зацикливайтесь на проблемах, которые отнимают слишком много времени. Решите как можно больше; затем вернитесь к остальным за то время, которое у вас осталось для этого теста.
Вам разрешается использовать калькулятор в этом тесте. Вы можете использовать свой калькулятор для решения любых задач по вашему выбору, но некоторые из них лучше всего решать без использования калькулятора.
Примечание. Если не указано иное, следует исходить из следующего.
- Иллюстративные фигуры НЕ обязательно выполнены в масштабе.
- Геометрические фигуры лежат на плоскости.
- Слово в строке обозначает прямую линию.
- Слово среднее обозначает среднее арифметическое.
Это действие откроет новое окно.Вы хотите продолжить?
Если вы заходите на этот сайт из-за пределов США, Пуэрто-Рико или территорий США, перейдите на неамериканскую версию нашего веб-сайта.
Верх
Причины выбора студентами STEM и связь выбора математики с поступлением в университет | Международный журнал STEM-образования
Аллен, К. Д., & Эйзенхарт, М.(2017). Борьба за желаемые версии будущего «я»: как молодые женщины договаривались о идентичностях, связанных с STEM, в дискурсивном ландшафте образовательных возможностей. Journal of the Learning Sciences, 26 (3), 407–436 Получено с https://doi.org/10.1080/10508406.2017.1294985.
Артикул Google ученый
Бандура, А. (1986). Социальные основы мысли и действия: социальная когнитивная теория . Энглвуд Клиффс, Нью-Джерси: Прентис-Холл.
Google ученый
Бильбао-Осорио, Б., Датта, С., и Ланвин, Б. (ред.). (2014). Глобальный отчет по информационным технологиям , 2014 Получено с https://core.ac.uk/download/pdf/30673033.pdf.
Blotnicky, K. A., Franz-Odendaal, T., French, F., & Joy, P. (2018). Исследование корреляции между знаниями в области STEM, самоэффективностью математики, карьерными интересами и карьерной деятельностью с вероятностью продолжения карьеры в STEM среди учащихся средней школы. Международный журнал STEM-образования, 5 (1), 22 https://doi.org/10.1186/s40594-018-0118-3.
Артикул Google ученый
Боттиа, М., Стернс, Э., Микельсон, Р., Моллер, С., и Валентино, Л. (2015). Выращивание корней специальностей STEM: женский факультет математики и естественных наук и участие студентов в STEM. Обзор экономики образования, 45 , 14–27. https://doi.org/10.1016/j.econedurev.2015.01.002.
Артикул Google ученый
Бричги В. (2014). Финский аттестат зрелости . Правление финского ME: Ylioppilastutkintolautakunta Получено с https://www.ylioppilastutkinto.fi/images/sivuston_tiedostot/Kehittaminen/YTL_presentation_English.pdf.
Google ученый
Каннади, М., Мур, Д., Вотруба-Дрзал, Э., Гринвальд, Э., Стайтс, Р., и Шунн, К. Д. (2017). Как личные, поведенческие и экологические факторы предсказывают работу в STEMM по сравнению с карьерой среднего уровня, не связанной с STEMM. International Journal of STEM Education, 4 (22) https://doi.org/10.1186/s40594-017-0079-y.
Кастаньо, К., и Вебстер, Дж. (2011). Понимание присутствия женщин в ИКТ: перспектива жизненного пути. International Journal of Gender, Science and Technology, 3 (2), 364–386 Получено с http: // genderandset.open.ac.uk/index.php/genderandset/article/view/168/333.
Google ученый
Сеси, С. Дж., И Уильямс, У. М. (ред.). (2007). Почему в науке мало женщин? Ведущие исследователи обсуждают доказательства . Вашингтон, округ Колумбия: Американская психологическая ассоциация Получено с http://scripts.cac.psu.edu/dept/cls/pubs/affiliated/valian/2006WomenAtTheTopInScience.pdf.
Google ученый
Чоу, А., Экклс, Дж., & Салмела-Аро, К. (2012). Профили ценности задач по предметам и стремлениям к физическим и ИТ-наукам в США и Финляндии. Психология развития, 48 (6), 1612–1628 Получено с https://psycnet.apa.org/doi/10.1037/a0030194.
Артикул Google ученый
Дэбни, К. П., Тай, Р. Х., Альмарод, Дж. Т., Миллер-Фридман, Дж. Л., Соннерт, Г., Сэдлер, П. М., и Хазари, З.(2012). Научная деятельность вне школы и ее связь с карьерным интересом в STEM. Международный журнал естественнонаучного образования, часть B , 2 (1), 63-79. DOI: https://doi.org/10.1080/21548455.2011.629455
Артикул Google ученый
Дасгупта, Н., и Стаут, Дж. Г. (2014). Девочки и женщины в науке, технологиях, инженерии и математике: развитие STEM и расширение участия в STEM-карьере. Policy Insights from the Behavioral and Brain Sciences, 1 (1), 21–29 Получено с https://journals.sagepub.com/doi/pdf/10.1177/2372732214549471.
Артикул Google ученый
Европейская комиссия (2019). Индекс цифровой экономики и общества (DESI ), получено с https://ec.europa.eu/digital-single-market/en/desi
Финляндия, С. (2017). Финляндия в цифрах , 2017 Получено с http: // tilastokeskus.fi / tup / suoluk / index_en.html.
Правительство Финляндии (2019) Соглашение о новой правительственной программе Финляндии . Получено с https://valtioneuvosto.fi/hallitusneuvottelut.
Министерство образования и культуры Финляндии (2017). Коротко о финском образовании . Получено из файла: /// C: /Users/skaattar/Downloads/finnish-education-in-nutshell.pdf
Holland, J. L. (1997). Выбор профессии: теория профессиональных личностей и рабочей среды (3-е изд.). Одесса, Флорида: Ресурсы психологической оценки.
Google ученый
Hübner, N., Wille, E., Cambria, J., Oschatz, K., Nagengast, B., & Trautwein, U. (2017). Максимизация гендерного равенства за счет минимизации вариантов выбора курса? Влияние обязательной курсовой работы по математике на гендерные различия в STEM. Journal of Educational Psychology, 109 (7), 993 Получено с https://doi.org/10.1037/edu0000183.
Артикул Google ученый
Янг, Х.(2016). Выявление STEM-компетенций 21 века с использованием данных о рабочих местах . Journal of Science Education and Technology, 25 (2), 284-301.pp 284-30. Получено с https://doi.org/10.1007/s10956-015-9593-1.
Артикул Google ученый
Lent, R. W., Brown, S. D., & Hackett, G. (1994). На пути к объединению социальной когнитивной теории карьеры и академического интереса, выбора и производительности. Журнал профессионального поведения, 45 (1), 79–122 Получено с https: // doi.org / 10.1006 / jvbe.1994.1027.
Артикул Google ученый
Линнансаари Дж., Вильяранта Дж., Лавонен Дж., Шнайдер Б. и Салмела-Аро К. (2015). Участие финских студентов в уроках естествознания. NorDiNa: Nordic Studies in Science Education, 11 (2), 192–206 Получено с https://www.journals.uio.no/index.php/nordina/article/view/2047.
Артикул Google ученый
Lin-Siegler, X., Ан, Дж. Н., Чен, Дж., Фанг, Ф. Ф. А., и Луна-Лусеро, М. (2016). Даже Эйнштейн боролся: влияние знаний о борьбе великих ученых на мотивацию старшеклассников изучать науку. Journal of Educational Psychology, 108 (3), 314 Получено с https://doi.org/10.1037/edu0000092.
Артикул Google ученый
Марго, К. К., и Кеттлер, Т. (2019). Восприятие учителями интеграции STEM и образования: систематический обзор литературы. International Journal of STEM Education, 6 (1), 2 Получено с https://doi.org/10.1186/s40594-018-0151-2.
Артикул Google ученый
Министерство образования и культуры (2016). PISA 2015: Финская молодежь все еще на вершине, несмотря на падение [Пресс-релиз]. Получено с https://ktl.jyu.fi/en/pressreleases/press-releases-2004/t061216.
Министерство образования и культуры (2017). Финская система образования. Получено с http://minedu.fi/en/education-system
Осборн, Дж., Саймон, С., и Коллинз, С. (2003). Отношение к науке: обзор литературы и ее значение. International Journal of Science Education, 25 (9), 1049–1079 Получено с https://www.tandfonline.com/doi/abs/10.1080/095006
00032199.
Артикул Google ученый
Пахарес, Ф., И Миллер, М. Д. (1994). Роль самоэффективности и убеждений в самооценке в решении математических задач: анализ пути. Journal of Educational Psychology, 86 (2), 193–203 Получено с https://doi.org/10.1037/0022-0663.86.2.193.
Артикул Google ученый
Pajares, F., & Urdan, T. C. (2006). Убеждения подростков в самоэффективности . Гринвич, Коннектикут: Издательство информационного века.
Google ученый
Палмер Т.А., Берк, П. Ф., и Обюссон, П. (2017). Почему школьники выбирают и отвергают науку: исследование факторов, которые учащиеся учитывают при выборе предметов. International Journal of Science Education, 39 (6), 645–662 Получено с https://www.tandfonline.com/doi/abs/10.1080/09500693.2017.1299949.
Артикул Google ученый
Паркер П., Марш Х., Чиаррочи Дж., Маршалл С. и Абдулджаббар А. (2014).Сопоставление математической самоэффективности и самооценки как предикторов долгосрочных результатов достижений. Педагогическая психология, 34 (1), 29–48 Получено с https://doi.org/10.1080/01443410.2013.797339.
Артикул Google ученый
Перес, Т., Кромли, Дж., И Каплан, А. (2014). Роль развития идентичности, ценностей и затрат в удержании STEM в колледже. Journal of Educational Psychology, 106 (1), 315–329 Получено с https: // psycnet.apa.org/doiLanding?doi=10.1037/a0034027.
Артикул Google ученый
Сейранян В., Мадва А., Дуонг Н., Абрамзон Н., Тиббетс Ю. и Харацкевич Дж. М. (2018). Продольные эффекты идентичности STEM и пола на процветание и достижения в физике в колледже. International Journal of STEM Education, 5 (1), 40 Получено с https://doi.org/10.1186/s40594-018-0137-0.
Артикул Google ученый
Славит, Д., Нельсон, Т. Х., и Лессей, К. (2016). Роль учителей в развитии, открытии и воспитании инклюзивной школы, ориентированной на STEM. International Journal of STEM Education, 3 (1), 7 Получено с https://doi.org/10.1186/s40594-016-0040-5.
Артикул Google ученый
Стадия, Ф. и Мэйпл, С. (1996). Несовместимые цели: рассказы о женщинах-выпускницах в математике. Американский журнал исследований в области образования, 33 (1), 23–51 Получено с http: // www.jstor.org/stable/1163379.
Артикул Google ученый
Су, Р., Раунды, Дж., И Армстронг, П. И. (2009). Мужчины и вещи, женщины и люди: метаанализ половых различий в интересах. Психологический бюллетень, 135 (6), 859 Получено с https://doi.org/10.1037/a0017364.
Артикул Google ученый
Välijärvi J., & Sulkunen S.(2016). Финская школа в международном сравнении. В Х. Ниеми, А., Тоом и А. Каллиониеми (ред.) Чудо образования (стр. 3-21). Роттердам, Нидерланды: Sense Publishers. https://doi.org/10.1007/978-94-6300-776-4_1
Глава Google ученый
Винсент-Руз, П., и Шунн, К. Д. (2018). Природа научной идентичности и ее роль как движущая сила выбора студентов. International Journal of STEM Education, 5 (1), 48 Получено с https: // doi.org / 10.1186 / s40594-018-0140-5.
Артикул Google ученый
Ван, М., и Дегол, Дж. (2016). Гендерный разрыв в науке, технологиях, инженерии и математике (STEM): текущие знания, значение для практики, политики и будущих направлений. Educational Psychology Review, 29 (1), 119–140 Получено с https://link.springer.com/content/pdf/10.1007/s10648-015-9355-x.pdf.
Артикул Google ученый
Ван, М.Т., и Дегол Дж. (2013). Мотивационные пути к выбору карьеры в STEM: использование перспективы и ценности для понимания индивидуальных и гендерных различий в областях STEM. Developmental Review, 33 (4), 304–340 Получено с https://doi.org/10.1016/j.dr.2013.08.001.
Артикул Google ученый
Ван М. Т., Экклс Дж. С. и Кенни С. (2013). Не отсутствие способностей, а больший выбор: индивидуальные и гендерные различия в выборе карьеры в области науки, технологий, инженерии и математики. Psychological Science, 24 (5), 770–775 Получено с https://doi.org/10.1177%2F0956797612458937.
Артикул Google ученый
Уильямс, К., Станисстрект, М., Сполл, К., Бойс, Э. и Диксон, Д. (2003). Почему школьники не интересуются физикой? Физическое образование, 38 (4), 324–329.
Артикул Google ученый
Wu, X., Дешлер, Дж. М., & Фуллер, Э. (2018). Влияние различных версий основного курса STEM на отношение и убеждения студентов. Международный журнал STEM-образования., 5 (44). https://doi.org/10.1186/s40594-018-0141-4.
Зельдин, А., и Пахарес, Ф. (2000). Несмотря ни на что: убеждения женщин в самоэффективности в математической, научной и технологической карьере. Американский журнал исследований в области образования, 37 (1), 215–246. https://doi.org/10.3102/00028312037001215.
Артикул Google ученый
Математические задачи в технике | Хиндави
Исследовательская статья
22 ноября 2021 г.
Оценка эффективности компьютерного обучения языкам с помощью анализа больших данных
Honglei Wang | Яньцзяо Ду | Sang-Bing Tsai
В этой статье представлено углубленное исследование и оценочный анализ влияния метода компьютерного обучения языку на изучение иностранного языка через его применение.Используя эмпирический исследовательский подход, было проведено практическое исследование компьютерного обучения английскому языку, чтобы проверить влияние CALL на устное изучение языка. Изучая влияние CALL на устное обучение студентов, включая влияние на беглость, точность и сложность устных выражений, а также влияние на отношение к обучению, CALL способствует повышению беглости устного выражения, сокращая количество паузы и повторения в устных выражениях, а также дать учащимся возможность осознанно использовать артикуляционные слова для облегчения плавного выражения.CALL хорош для повышения точности речи учащихся, но он не играет значительной роли в грамматической точности, а грамматические ошибки в основном проявляются в третьем лице единственного числа глаголов, единственном и множественном числе существительных и пассивном залоге. Использование CALL при обучении устной речи не улучшает разнообразие предложений. Однако применение CALL в устном обучении стимулирует энтузиазм студентов к обучению, повышает их интерес к изучению разговорного английского языка и повышает их уверенность в устном выражении.
Исследовательская статья
22 ноября 2021 г.
Моделирование гигромеханического поведения волокон Raffia vinifera во время явления диффузии воды
Harrond Nimjieu Takoudjou | Никодем Р. Сикаме Тагне | … | Ebenezer Njeugna
В промышленных условиях, где поощряется использование экологически чистых материалов, натуральные волокна растительного происхождения становятся все более востребованными для армирования композитных материалов. Эта работа посвящена моделированию гигромеханического поведения волокна из рафии и винифера во время явления диффузии.Моделирование диффузии воды через волокно рафии vinifera описывается вторым законом Фика с учетом явления набухания волокна. Полученное уравнение решается численно методом конечных разностей и получается зависимость радиуса волокна от времени. Применяя правило интегрирования Лейбница, предлагается математическое выражение для предсказания эволюции этого радиуса как функции времени. Численно и аналитически наблюдается увеличение безразмерного радиуса волокна со временем до критического значения, после чего наблюдается насыщение.Эта модель позволила нам предложить математическую модель, описывающую кинетику поглощения волокна рафии vinifera через его коэффициент поглощения. Сравнивая результаты этой модели с экспериментальными результатами из литературы, можно наблюдать хорошее согласие. Более того, индуцированные напряжения в волокне во время диффузии воды также могут быть оценены с помощью предложенного выражения математической модели волокна. Эти напряжения увеличиваются со временем и могут достигать 5-7 ГПа.Результаты этой работы могут быть использованы для прогнозирования поведения волокна рафии и винифера внутри композитного материала во время его разработки.
Исследовательская статья
22 ноября 2021 г.
Новый эффективный пересчитывающийся M-оценщик для надежной подгонки моделей линейной регрессии при наличии выбросов
Дост Мухаммад Хан | Мухаммед Али | … | Sundus Hussain
Устойчивая регрессия – это важная итерационная процедура, которая направлена на анализ наборов данных, загрязненных выбросами и необычными наблюдениями, и уменьшение их влияния на коэффициенты регрессии.Для решения проблемы выбросов и обеспечения эффективных и стабильных оценок в их присутствии были введены надежные методы оценки. В литературе были разработаны различные робастные оценки, чтобы ограничить неограниченное влияние выбросов или точек рычага на оценки модели. Здесь предлагается новая восходящая M-оценка с использованием новой целевой функции с основным упором на получение высоконадежных и эффективных оценок, дающих многообещающие результаты. Из результатов очевидно, что для нормальных и чистых данных предлагаемая оценка почти так же эффективна, как и обычный метод наименьших квадратов, и, тем не менее, становится очень устойчивой к выбросам, когда она используется для загрязненных наборов данных.Имитационное исследование проводится для оценки эффективности предлагаемой нисходящей M-оценки по различным сценариям генерации данных, включая нормальное, t -распределение и двойное экспоненциальное распределение с различными уровнями загрязнения выбросов, и результаты сравниваются с существующие нисходящие М-оценки, например, функции Хубера, Тьюки Бивеса, Хэмпеля и Эндрю-Знака. Эффективность предлагаемых оценщиков была также проверена с использованием реальных данных оценщиков, и было обнаружено, что предложенные оценщики дают многообещающие результаты по сравнению с существующими оценщиками.
Исследовательская статья
22 ноября 2021 г.
Об отказоустойчивом разделении однородных графов Caterpillar
Камран Ажар | Сохаил Зафар | Ага Кашиф
Параметры, связанные с метрикой в теории графов, имеют несколько приложений в робототехнике, навигации и химических слоях. Важным таким параметром является размер раздела графов, который играет важную роль в инженерии, информатике и химии. В контексте химической и фармацевтической инженерии эти параметры используются для уникального представления химических соединений и их структурного анализа.Структура молекул бензоидных углеводородов представлена в виде гусеничных деревьев и изучается по различным характеристикам, включая спектр поглощения УФ, молекулярная восприимчивость, анизотропия и теплота атомизации. Несколько классов деревьев были изучены на предмет размерности разбиения; однако в этом отношении еще предстоит изучить расширенный вариант – измерение отказоустойчивого раздела. В этой статье мы вычислили размерность отказоустойчивого разбиения для однородных гусениц,, и для,, и, соответственно, и оказалось, что она постоянна.Дополнительные числовые примеры и приложение предоставлены для уточнения точности и значимости работы.
Исследовательская статья
20 ноября 2021 г.
Применение интеллектуального анализа данных в сочетании с нечетким многокритериальным принятием решений при оценке кредитного риска юридическими компаниями
Jianmiao Hu | Чонг Чен | Kongze Zhu
Цель состоит в том, чтобы предотвратить систематические финансовые риски из-за финансового пузыря Интернета и повысить эффективность оценки кредитных рисков юридических компаний.Во-первых, это исследование анализирует обычно используемую модель классификации, машину опорных векторов (SVM) и модель линейной регрессии, логистическую модель, а затем предлагает интегрированную SVM-логистику + нечеткое многокритериальное принятие решений (FMCDM) для оценки и анализа кредита. уровень риска листинговых компаний. В предлагаемой интегрированной модели модель SVM классифицирует выборку данных из листинговых компаний, а логистическая модель используется для регрессионного анализа оценки кредитного риска. На основе индексов кредитного риска и факторов неопределенности весов отобранных компаний, FMCDM на основе нечеткого набора применяется для получения индексов оценки.Затем для получения веса ключевых индексов используется процесс аналитической иерархии (AHP). Наконец, анализ соответствия выполняется в соответствии с существующим статусом риска выбранной компании и результатами статуса риска предложенной интегрированной модели. Результаты показывают, что интегрированная модель SVM-Logistic является дополнительной и имеет высокую интенсивную оценку. Согласно значению пригодности, полученному FMCDM, можно точно оценить статус кредитного риска компании, а промежуточный порог измерения риска корпоративного кредитного дефолта равен 0.56152; если Fit ниже порогового значения, рейтинг компании низкий, а если Fit выше порогового значения, рейтинг компании высокий. Таким образом, технология интеллектуального анализа данных, основанная на интегрированной модели SVM-Logistic + FMCDM, имеет высокую точность и возможность применения при оценке кредитного риска юридическими компаниями. Это исследование создает новую методическую модель для компаний, оказывающих юридические услуги в области оценки корпоративного кредитного риска, и может предоставить ссылки и идеи для оценки корпоративного кредитного риска.
Исследовательская статья
20 ноября 2021 г.
Исследование потока жидкости магнитных / немагнитных наночастиц под действием нелинейного теплового излучения
Айеша Шаукат | Мухаммад Муштак | … | Рана Мухаммад Акрам Мунтазир
Настоящая исследовательская работа исследует численный перенос тепла в конвективном пограничном потоке, имеющем характеристики магнитных () и немагнитных () наночастиц, синтезированных в два разных типа ньютоновских (вода) и неньютоновских (альгинат натрия) конвективных оснований. жидкости кассона наножидкости, которые объединяют захватывающие эффекты нелинейного теплового излучения и магнитного поля, встроенного в пористую среду.Характеристики вязкой несжимаемой жидкости, передаваемой электрическим током, учитываются в рамках модели жидкости Кэссона. Математическая формулировка управляющих дифференциальных уравнений в частных производных (PDE) с высокой степенью нелинейности преобразуется в обыкновенные дифференциальные уравнения (ODE) с использованием подходящего преобразования подобия, которое составляет безразмерные соответствующие параметры. Преобразованные ОДУ решаются численно путем реализации в MATLAB. Графическая иллюстрация с целью улучшения численных расчетов режима потока предусмотрена для заданных параметров, соответствующих различным профилям (скорость и температура).Чтобы уточнить поведение Нуссельта и коэффициента поверхностного трения, анализируется табличная демонстрация различных конкретных параметров. Считается, что градиент скорости ньютоновских жидкостей намного выше по сравнению с неньютоновскими жидкостями.
