Урок математики по теме “Как мы будем сравнивать”
Урок математики в 1 классе (УМК «Планета знаний») по теме
«Как мы будем сравнивать»
Цели: Ознакомление с признаками, по которым сравнивают предметы: форма, размер, цвет, количество, расположение.
Универсальные учебные действия:
Познавательные: сравнивать изображенные предметы, находить сходства и отличия; умение пересчитывать предметы на рисунке, формирование представлений об отношениях «перед», «между», «за», «под», «над».
Регулятивные: следовать указаниям учителя при организации работы, организовывать свое рабочее место.
Коммуникативные: умение слушать учителя, отвечать на поставленный вопрос, высказывать предположение.
Ход урока
1. Организация начала урока.
– Сегодня мы продолжаем путешествие по Планете знаний.
На уроке вы узнаете много нового и интересного. Давайте проверим вашу готовность к уроку. У вас должны быть приготовлены учебник, тетрадь, ручка, цветные карандаши.
2. Мотивация.
– Урок сегодня очень серьёзный и насыщенный. Сегодня у нас в гостях Мудрая Сова. Кого называют мудрым? Мудрый – очень опытный, умный, готовый дать полезный совет. Что она держит? Она держит книгу, на которой написано какое-то напутствие!
(читающий ученик читает «Вперёд за знаниями!»)
– Итак, отправляемся за знаниями!
3. Открытие новых знаний.
1) – Сова приглашает нас в свой мир – мир животных. Рассмотрите изображения на слайде (Приложение 1). Кого вы видите? Сколько всего животных? Сосчитаем хором!
– Ответьте на вопросы:
– Сколько бабочек? Какая бабочка красивее? На этот вопрос однозначно ответить нельзя. Кому-то нравится первая бабочка, кому-то вторая.
Сравнивать по красоте нельзя.
– Чем они похожи? (формой, размером)
– Чем отличаются? (цветом)
– Как, по каким признакам мы сравнивали? (по форме, размеру и цвету)
– Назовите самого сильного животного. Можно ли льва, слона, тигра сравнивать по силе? (нельзя).
– Кто больше: слон или тигр? Кто меньше: тигр или мышь? По каким признакам можно ещё сравнивать этих животных? ( по количеству ног, по цвету и пр.)
– Итак, мы будем их сравнивать по размеру, форме, цвету.
– Рассмотрите слайд 2. Что это? Как называются эти цветы? Сколько их?
– Чем они похожи? (формой, размером)
– Чем отличаются? ( одна -красная, вторая – желтая, отличаются цветом).
– Рассмотрите следующий рисунок. Чем похожи эти розы? (цветом и размером)
– Чем же они отличаются? ( они отличаются формой)
– Сравним следующую пару цветов.
Чем похожи они? (цветом, формой)
– Чем отличаются? (размером: первая роза гораздо больше, чем вторая).
– Итак, подведём итог. По каким признакам мы сравнивали объекты? (Сравнивали по цвету, форме, размеру).
– Мудрая Сова довольна нашими результатами и приготовила для нас весёлую музыкальную физминутку.
Музыкальная физминутка
2) – Ребята, у каждого на парте появился конверт. Давайте посмотрим, что там находится. Выложите содержимое конвертов. ( В конверте 3 полоски разного цвета и разной длины и ширины).
– Чем похожи все эти полоски? (формой)
– Чем отличаются полоски? (цветом и размером).
– Покажите полоски одинакового цвета. Сравните их. Покажите полоску, которая шире. – – Покажите полоску, которая уже.
– Покажите самую длинную полоску. Покажите полоску, которая короче её. Самую короткую.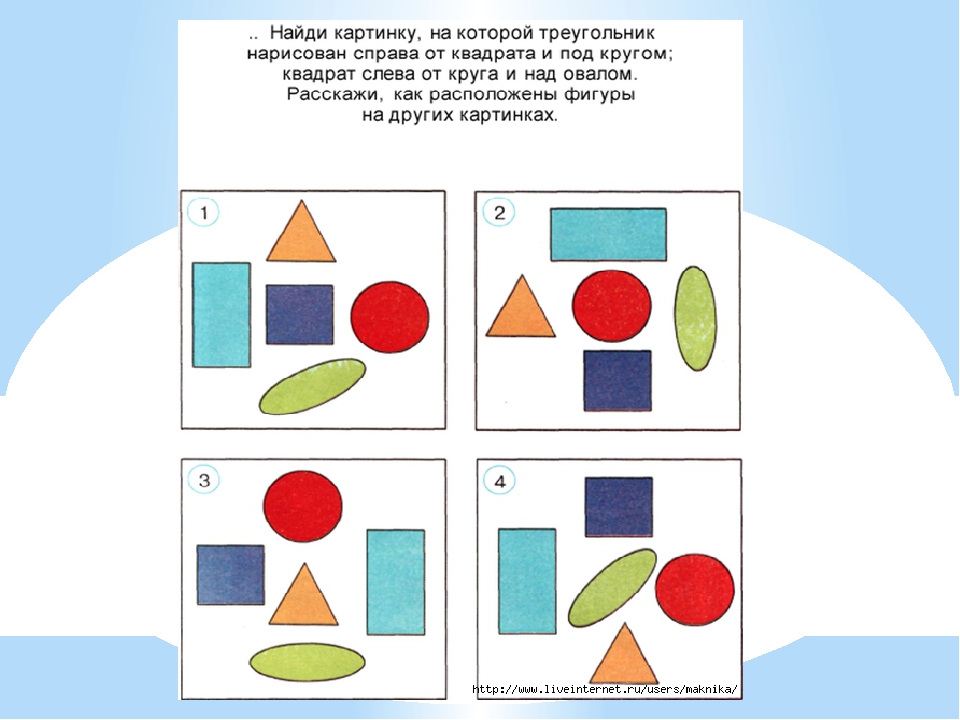
– По каким признакам мы сравнивали полоски? (по цвету, форме, ширине и длине)
– Мы хорошо поработали, уберите полоски в конверты).
3) –Поработаем с учебником. Откройте страницу 5. Вспомним, как правильно листать страницы, как обращаться с учебником.
– Найдите задание 4. Что вы видите? Это игрушки.
– Сколько игрушек изображено на рисунке? Ребята, это-множество игрушек.
– На какие группы можно разделить это множество игрушек? (машинки, куклы, мяч).
– Каких игрушек много? Сколько их?
– Каких игрушек мало? Сколько мячей?
– Каких игрушек больше всего? Меньше всего?
– По какому признаку мы сейчас сравнивали предметы? (по количеству)
– Рассмотрите рисунок 5. Что вы видите за домом? Перед домом? Кто стоит между мамой и папой? Кто ближе всех к дедушке? Дальше всех от дедушки? Молодцы, очень хорошо отвечали на вопросы.
Закройте учебники.
– Мы проделали очень большую работу, и Сова предлагает нам отдохнуть.
Физминутка
4) – А теперь самое время поработать в тетрадях. Откроем страницу 4. Рассмотрите внимательно рисунок. Что вы видите?
– Что стоит на столе? Сколько чашек стоит на столе? (3) Раскрасьте чашки красным карандашом.
– Что вы увидели под столом? Раскрасьте эти предметы синим цветом.
– Что висит над столом? Раскрасьте зелёным цветом.
– Покажите свою работу соседу по парте. Если вам понравилась работа товарища-похвалите его.
4. Рефлексия.
– Давайте подведём итог. По каким же признакам можно сравнивать предметы?
– Интересен ли был для вас урок? Чем? Что особенно понравилось? Кого вы бы отметили сегодня на уроке?
Список литературы:
1.
Башмаков М.И. Нефедова М.Г. Математика. Учебник 1-4 класс. В 2-х частях Москва. АСТ, Астрель 2011.
2.Башмаков М.И. Нефедова М.Г. Математика. Рабочая тетрадь .№ 1, №2 1-4 класс Москва. АСТ, Астрель 2011.
3..Башмаков М.И. Нефедова М.Г.Обучение в 1-4 классе по учебнику “Математика” Москва. АСТ, Астрель 2011.
4.Как проектировать универсальные учебные действия в начальной школе. От действия к мысли. Серия: Стандарты второго поколения. Изд. Просвещение, 2011.
5.Примерные программы по учебным предметам. Начальная школа. В 2-х частях Серия: Стандарты второго поколения. Изд. Просвещение, 2013.
6.Федеральный государственный образовательный стандарт начального общего образования. Серия: Стандарты второго поколения. Изд. Просвещение, 2012.
Сравнение чисел – методика, примеры (6 класс, математика)
4.4
Средняя оценка: 4.4
Всего получено оценок: 873.
4.4
Средняя оценка: 4.4
Всего получено оценок: 873.
В реальной жизни часто нужно производить сравнение чисел.
Сравнивать положительные числа все умеют с детства. В данной статье подробно рассказывается, как сравнить любые два числа, в том числе имеющие разные знаки.
Какое число больше
Проведем координатную ось: отметим на прямой точку начала координат (число 0), выберем масштабную единицу и направление.
Рассмотрим два числа a и b. Изобразим на координатной оси точки, соответствующие в выбранном масштабе данным числам.
Из двух чисел большим будет то, которое расположено правее на координатной оси.
Рис. 1. Сравнение двух чисел.Пример
Рассмотрим числа -1 и 2 и соответствующие им точки на координатной оси.
Рис. 2. Сравнение чисел -1 и 2.Поскольку число 2 на координатной оси лежит правее числа -1, оно является большим из этих двух чисел.
Обозначение: 2 > -1.
Положительные и отрицательные числа
Все числа, которые на координатной оси лежат правее нуля, называются положительными.
Все числа, которые на координатной оси лежат левее нуля, называются отрицательными.
Число нуль не является ни положительным, ни отрицательным, а его название в переводе с латинского означает «никакой». Впервые нуль как число начали использовать в Индии. А древние римляне, китайцы и греки обходились без него. А в древнем Египте, хотя и не использовали нуль, но обозначали его иероглифом, который означал «прекрасный».
Понятие отрицательного числа ввели китайские математики. Положительные числа они обозначали палочками красного цвета, а отрицательные – палочками черного цвета. Необходимость ввести отрицательные числа возникла при проведении финансовых расчетов. Они использовались при подсчете долгов.
Методика сравнения двух чисел
Рассмотрим возможные случаи сравнения двух чисел. Обозначим их, как a и b.
1) Пусть одно из чисел (a) является положительным, а другое (b) – отрицательным. Тогда бОльшим будет положительное число: a > b.
Таким образом, любое положительное число больше любого отрицательного.
Пример
Сравним числа 5 и -7.
Имеем: 5 > -7.
2) Из двух отрицательных чисел меньшим будет то число, модуль которого больше.
Пример
Сравним числа -5 и -7.
Модуль числа -5 равен 5, а модуль числа -7 равен 7. Поскольку 7 > 5, -7 < -5.
Имеем: -5 > -7.
3) Любое положительное число больше 0, а любое отрицательное число меньше 0.
Пример
Рассмотрим числа 3 и -2. Имеем: 3 > 0, -2 < 0.
Неотрицательные и неположительные числа
Все положительные числа и нуль называются неотрицательными.
Все отрицательные числа и нуль называются неположительными.
Пример
Изобразим на координатной оси отрезок, начало которого лежит в точке -2, а конец – в точке 3.
Рис. 3. Отрезок на числовой прямой.Будем рассматривать целые числа внутри данного отрезка. Из них:
- положительные числа 1, 2, 3;
- неотрицательные числа 0, 1, 2, 3;
- отрицательные числа -2, -1;
- неположительные числа -2, -1, 0.
Сравнение дробей
Чтобы сравнить две дроби одного знака, нужно привести их к общему знаменателю.
Пример
Сравним числа ${2 \over 3} и {5 \over 9}$.
Приведем эти числа к общему знаменателю (9): ${2 \over 3} = {6 \over 9}$.
Поскольку ${6 \over 9} > {5 \over 9},$ имеем: ${2 \over 3} > {5 \over 9}$.
Двойные неравенства
Пусть для числа a одновременно выполняется два неравенства: a > 6 и a < 10. Тогда можно написать двойное неравенство
6 < a < 10 .
Что мы узнали?
Мы ввели правило сравнения двух чисел с помощью точек на координатной оси. Также мы рассмотрели определения отрицательного, положительного, неотрицательного и неположительного числа. Затем мы рассмотрели все возможные случаи сравнения чисел с учетом их знака.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Александр Митченко
5/5
Николай Андреев
5/5
Виктор Оськин
5/5
Мария Котова
5/5
Никита Поцелуев
5/5
Паша Бойцов
4/5
Ольга Румянцева
4/5
Максим Быков
5/5
Галина Садыкова
5/5
Валентина Белоусова
5/5
Оценка статьи
4Средняя оценка: 4.4
Всего получено оценок: 873.
А какая ваша оценка?
Точки и квадратики – Математика для учителей начальных классов
Числа и операции
Предположим, вас попросили вычислить 3906 ÷ 3. Один из способов интерпретации этого вопроса (есть и другие):
«Сколько групп по 3 вписывается в число 3906?»
Определение
В квотной модели деления вам дается дивиденд (здесь это 3906), и вас просят разделить его на группы равного размера, где размер группы определяется делитель (здесь это 3).
В нашей модели точек и прямоугольников делимое 3906 выглядит следующим образом:
и три точки выглядит так:
Итак, мы действительно просим:
«Сколько групп вписывается в картинку 3906?»
Пример: 3906 ÷ 3
Существует одна группа из 3 на уровне тысяч и три на уровне сотен, ни одной на уровне десятков и две на уровне единиц.
Обратите внимание, что у нас на картинке:
• Одна группа из 3 в поле тысяч.
• Три группы по 3 в поле сотен.
• Нулевые группы по 3 в поле десятков.
• Две группы по 3 штуки в коробке для единиц.
Это показывает, что 3 входит в число 3906 одну тысячу, три сотни и две единицы раз. То есть
Попробуем посложнее! Рассмотрим 402 ÷ 3. Вот картинка:
Мы все еще ищем группы из трех точек:
Определенно есть одна группа на уровне 100.
, и теперь, кажется, мы застряли, групп по три больше нет!
Подумай / Соедини / Поделись
Что мы можем сделать сейчас? Мы действительно застряли? Сможете решить задачу на деление?
Пример: 402 ÷ 3
Вот детали, разработанные для 402 ÷ 3. Но не читайте это, пока не подумаете об этом сами!
Так как каждая точка соответствует десяти точкам в поле справа, мы можем написать:
Теперь мы можем найти больше групп из трех:
До сих пор есть лишняя точка.
Давайте разобьем его тоже
Это даст нам больше групп из трех:
На картинке у нас есть:
• Одна группа из 3 в поле сотен.• Три группы по 3 в поле десятков.
• Четыре группы по 3 штуки в коробке для единиц.
Наконец-то у нас есть ответ!
Подумай / Соедини / Поделись
Решите каждое из этих упражнений, используя метод точек и прямоугольников:
62124 ÷ 3 61230 ÷ 5
Пример: 156 ÷ 12
Давайте увеличим сложность на ступеньку выше. Рассмотрим 156 ÷ 12. Здесь мы ищем группы по 12 на этой картинке:
Как выглядит 12? В одной ячейке может быть двенадцать точек:
Но чаще всего мы записываем 12 так, как десятку и 2 единицы:
Некоторые из них мы, безусловно, видим на картинке. На уровне десятков наверняка есть один:
Примечание: При отсутствии взрыва это будет двенадцать точек в поле десятков, поэтому мы отмечаем одну группу из 12 над полем десятков.
Мы также видим три группы из двенадцати единиц:
Итак, на картинке мы имеем:
• Одна группа из 12 точек в поле десятков.
• Три группы по 12 точек в блоке единиц.
Значит
156 ÷ 12 = 13.
Задача 6
Используйте модель точек и прямоугольников для вычисления каждого из следующего:
13453 ÷ 11
4853 ÷ 23
214506 ÷ 102
Задача 7
Помните, что числа с основанием пять находятся в системе 1 ← 5 точек и квадратов. Каковы значения места в системе 1 ← 5? Заполните пробелы:
- Нарисуйте число в точках и квадратиках .
- Нарисуйте число в виде точек и прямоугольников .
- Используйте метод точек и прямоугольников, чтобы найти .
- Перепишите предложение о делении в десятичной системе счисления и проверьте правильность.
- Используйте точки и прямоугольники, чтобы найти .
Не преобразовывать в 10-ю систему!
Не преобразовывать в 10-ю систему!
Подумай / Соедини / Поделись
- Используйте точки и прямоугольники для их вычисления.
2130 ÷ 10
41300 ÷ 100
- Какие картинки вы использовали для 10 и 100? Можете ли вы описать словами, что происходит при делении на 10 и на 100 и почему?
Мы использовали точки и прямоугольники, чтобы показать, что 402 ÷ 3 = 134.
В начальной школе вы, возможно, научились решать эту задачу на деление, используя схему, подобную следующей:
На первый взгляд это кажется очень загадочным, но на самом деле это ничем не отличается от метода точек и прямоугольников. Вот что означает таблица.
Чтобы вычислить 402 : 3, мы сначала делаем большую оценку того, сколько групп по 3 есть в 402. Давайте предположим, что есть 100 групп по три.
Сколько осталось после удаления 100 групп по 3 человека? Мы вычитаем, чтобы найти, что осталось 102.
Сколько групп по 3 в числе 102? Попробуем 30:
Сколько осталось? Осталось 12 и есть четыре группы по 3 в 12.
На это приходится все число 402. И где нам найти окончательный ответ? Просто добавьте общее количество групп из трех, которые мы подсчитали:
.402 ÷ 3 = 100 + 30 + 4 = 134.
Подумай / Соедини / Поделись
- Сравните две приведенные ниже диаграммы делений. В чем они одинаковы? Чем они отличаются?
- Также обратите внимание на метод точек и прямоугольников. В чем она совпадает или отличается от двух диаграмм?
- Почему нам нравится стандартный алгоритм? Потому что это быстро, не так много нужно записать, и это работает каждый раз.
- Почему нам нравится метод точек и прямоугольников? Потому что это легко понять. (А рисовать точки и прямоугольники — одно удовольствие!)
Мы видели, что 402 делится на 3 без остатка: 402 ÷ 3 = 134.
Это означает, что 403, еще одно, не должно делиться на три. Это должно быть на одну точку больше.
Пример: 403 ÷ 3
Увидим ли мы лишнюю точку, если вычислим 402 ÷ 3 с точками и прямоугольниками?
Да, есть! У нас осталась одна точка в конце, которую нельзя разделить. Вот как это выглядит в стандартном алгоритме.
В школе мы говорим, что у нас есть остаток от единицы, а иногда пишем:
Но что это на самом деле означает? Это означает, что у нас есть 134 группы по три с одной точкой. Так
Пример: 263 ÷ 12
Попробуем другой: 263 ÷ 12. Вот что у нас есть:
И мы ищем такие группы:
Вот так!
Unexploding больше не поможет, и у нас действительно останется одна оставшаяся точка в позиции десятков и точка в позиции единиц. У нас есть 21 группа из двенадцати человек и остальные из одиннадцати.
Подумай / Пара / Поделись
- Используйте метод точек и прямоугольников для вычисления каждого частного и остатка:
5210 ÷ 4
4857 ÷ 23
31533 ÷ 101
- Теперь используйте стандартный алгоритм (пример показан ниже) для вычисления каждого из приведенных выше частных и остатков.
- Какой метод вам больше нравится: точки и прямоугольники или метод стандартного алгоритма? Или это зависит от проблемы, которую вы решаете?
Стадия 1 Ресурс математического мышления – 6 против 6
Итак, математики, с возвращением! Пришло время подготовить ваши глазные яблоки к тщательному исследованию двух коллекций 6 против 6.
Итак, вам понадобится бумага и карандаш. Итак, прежде всего, что вы заметили в этих двух коллекциях из 6, что отличается?
Вы видите что-то другое? Отлично, можешь записать? Запишите это или нарисуйте то, что, как вы заметили, отличается между двумя коллекциями.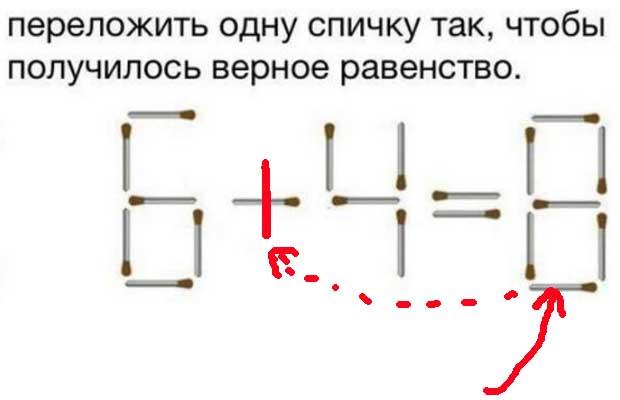
Да, и если вы подумали об одной вещи, которая отличается, можете ли вы теперь придумать другую вещь, которая отличается между этими двумя коллекциями из шести?
И это тоже можно записать или нарисовать. Да, ты прав. потому что математики представляют идеи множеством разных способов. Хорошо, теперь у меня к вам другой вопрос. Что-то, что вы заметили, это одно и то же?
Да. Итак, если у вас есть одна такая же вещь, можете ли вы придумать вторую такую же вещь?
Да, и это тоже запиши или нарисуй. Хорошо, поговорим вместе, поэтому мы также поговорили с некоторыми молодыми математиками, и вот некоторые идеи, которые они придумали. Таким образом, одна из особенностей, которую они заметили, заключается в том, что одна из коллекций показывает, что 6 является двойным фактом. Вы знаете 2 тройки.
Но другая коллекция показывает, что 6 в этом представлении показывает шаблон сокращения, где 6 равно 3, а 2 и еще 1.
Да, я бы хотел посчитать в обратном порядке 3, 2, 1.
Угу. И на самом деле, что нам, математикам, вероятно, следует сделать, прежде чем мы двинемся дальше, так это то, что мы могли бы использовать таблицу для организации идей, чтобы она не выглядела довольно беспорядочно. Итак, нарисуем таблицу. И да, вы правы, математики часто используют таблицы, чтобы систематизировать информацию и идеи. Так легче читать, а также делиться с другими людьми, хорошо!
А что насчет одинаковых вещей? Вот некоторые идеи, которые у нас были. Во-первых, в обеих коллекциях было 6 точек, а во-вторых, обе они показали, что внутри 6 есть один столбец из 3. Вы видите это? Да, синий столбец на, например, лестнице, сжимающемся шаблоне или сжимающемся представлении 6, а затем синий столбец, а также зеленый столбец на другом представлении 6, который показывает 6, является двойным 3.
Хорошо! Да, мы также заметили, что обе коллекции одинаковы: 6 — это 2 тройки. Да, и в одном представлении лестницы мы видим 3 как один столбец 3 в синем и треугольнике.
Треугольник в зелени.
И да, у вас мог бы быть треугольник вверху, а затем вместо столбца у вас мог бы быть ряд из 3 внизу, а в другом мы можем видеть 2 тройки. Это также легче объяснить. Да, вы правы, но 2 тройки разные. Да, так что один из трех.
Одна из коллекций, похожая на 6 на кубике, имеет 2 тройки в виде двух столбцов по три, а другая состоит из трех в виде треугольника и трех в виде строки или столбца. в зависимости от того, как вы на это смотрите. Да, да, и еще одна вещь, о которой мы подумали, это то, что 6, если вы посмотрите на эту версию 6, также может показать, что это 3 двойки, 2 вверху, 2 в середине и 2 внизу.
Хорошо, тогда у меня есть еще кое-что, о чем вы можете подумать. Когда мы смотрим на эту коллекцию, эти две коллекции, которая лучше всего показывает 6, могут быть сделаны путем удвоения 3, по вашему мнению. Вы можете указать на это?
Да, мы тоже так подумали, потому что у него 2 мм, 2 столбца, и у них одинаковое число в каждом столбце в 3 рядах по 2.