Куда можно поступить с физикой и профильной математикой? ПрофГид
Автор: ПрофГид
Обновлено
Профильная математика и физика – классические инженерные предметы для ЕГЭ, с которыми открываются широкие возможности для поступления. Но как выбрать ту специальность, которая подходит именно тебе? Мы предлагаем 3 наиболее востребованных и перспективных варианта, а ты постарайся понять, нравится ли тебе какой-то из них. Кстати, недавно центр профориентации ПрофГид разработал точный тест на профориентацию, который сам расскажет, какие профессии вам подходят, даст заключение о вашем типе личности и интеллекте.
Читайте также :
Наноинженерия
Код: 28.03.02
Профессии: инженер в области нанотехнологий, инженер-технолог в области нанотехнологий, нанотехнолог, наноспециалист, наноинженер, инженер-электроник.
Нанотехнологии – это то, что когда-то казалось невероятным и далеким, а сегодня превратилось в одну из наиболее востребованных отраслей науки и техники.
- подготавливать и проводить исследования в области наноинженерии;
- проектировать нанообъекты и проводить расчетные работы для этого;
- проводить исследования, направленные на усовершенствование уже имеющихся разработок в области нанотехнологий;
- создавать техническую документацию для изделий, созданных на основе нанообъектов;
- управлять технологическими системами, которые используются при производстве нанообъектов.
Если говорить более конкретно о том, куда поступить с физикой и математикой по такому профилю, то ты можешь выбрать Московский государственный технический университет им. Н.Э. Баумана. Здесь предусмотрено 60 бюджетных мест по специальности «Наноинженерия», а проходной балл составляет от 73.
Машиностроение
Код: 15.03.01
Профессии: инженер нефтеперерабатывающих заводов, дефектоскопист, инженер-материаловед, инженер по технике безопасности, инженер-сварщик.
Читайте также :
Этот вариант того, куда можно поступить с математикой и физикой, подходит любителям инженерного дела и машиностроительных предприятий. Специалисты в подобной области занимаются разработкой, ремонтом, усовершенствованием и настройкой работы различных машин и механизмов, следят за производственным процессом, проводят экспертизы и управляют сотрудниками предприятий. Чтобы изучить этот профиль, тебе придется освоить:
- обслуживание технического оборудования, его настройку, испытание, установку, ремонт;
- составление проектной и технической документации для разрабатываемого, устанавливаемого и обслуживаемого оборудования;
- проведение расчетов и создание проектов машиностроительных узлов, их деталей и конструкций;
- проверку соответствия оборудования и технологических процессов установленным нормам;
- управление небольшими коллективами.
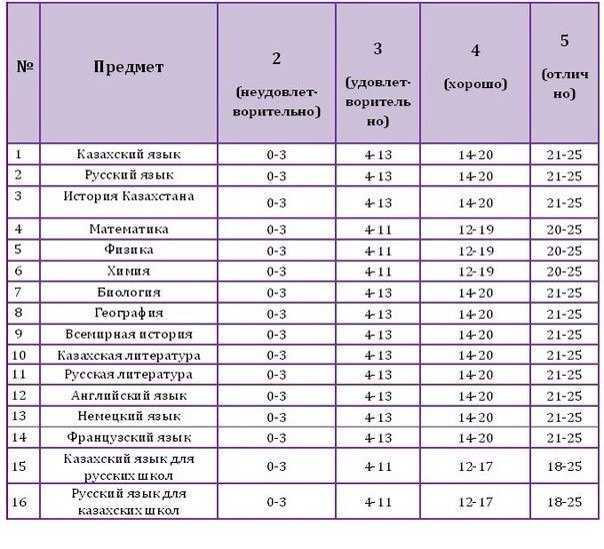
В Москве пройти обучение по такому профилю можно, например, в Российском государственном университете нефти и газа им. И.М. Губкина. Здесь предусмотрены 22 бюджетных места, форма обучения – очная, а проходной балл составляет 76.7. Один из других вариантов – Санкт-Петербургский горный университет, также с очной формой получения образования, с 25 бюджетными местами и с проходным баллом, составляющим 68.3.
Строительство
Код: 08.03.01
Профессии: архитектор, градостроитель, ландшафтный архитектор, инженер-строитель, инженер транспортного строительства, инженер-проектировщик, строитель, эколог градостроительства.
Это направление, в котором можно выделить внушительное число узких специализаций. Например, ты можешь сконцентрироваться на архитектуре и реставрации, на транспорте, на проектировке ландшафта, на облицовочных или отделочных работах, и так далее. Если же у тебя пока нет четкого представления о том, чем из внушительной области строительства ты хотел бы заниматься, можно выбрать более общий профиль. В любом случае, в вузе тебе придется изучить:
В любом случае, в вузе тебе придется изучить:
- разработку проектов будущих зданий и сооружений;
- контроль за соответствием строительного процесса проектной документации;
- возведение зданий и сооружений, установку, налаживание и обслуживание строительных объектов и инженерных коммуникаций;
- проведение строительной экспертизы;
- реконструкцию и реставрацию зданий и сооружений.
Чем особенно хорош этот вариант того, куда можно поступить с физикой и профильной математикой – так это большим выбором вузов и внушительным количеством бюджетных мест. Так, в столице подготовкой кадров по этой специальности занимается, в том числе, Национальный исследовательский Московский государственный строительный университет. Он предлагает 800 бюджетных мест, очную форму обучения, а проходной балл здесь составляет 67.3. В северной столице ты можешь обратить внимание, например, на Санкт-Петербургский политехнический университет Петра Великого.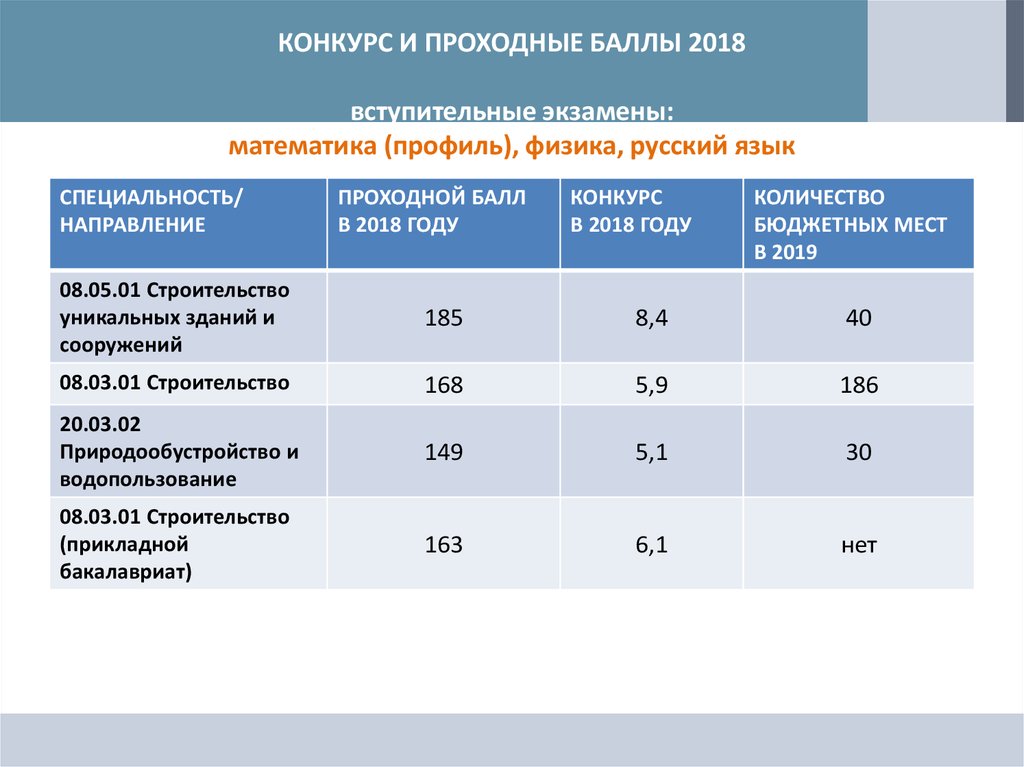
Мы очень надеемся, что ты сумеешь сделать правильный выбор и обучиться профессии, которая будет доставлять тебе удовольствие!
Читайте также :
выбрать профессию в вузах России
Войдите или зарегистрируйтесь, чтобы открыть доступ к новым функциям
- Регистрация
- Вход
Восстановить пароль
Напомнить логин
*В логине разрешены латинские буквы/цифры/точка/@
Выберите город, в который хотите поступатьАбаканАлександровАлексеевкаАльметьевскАнапаАнгарскАнжеро-СудженскАпатитыАргунАрзамасАрмавирАрмянскАрхангельскАстанаАстраханьБакуБалаковоБалашихаБалашовБарнаулБатайскБелгородБелогорскБелорецкБелоярскийБердскБерезникиБийскБиробиджанБлаговещенскБокситогорскБратскБрянскБугульмаБугурусланБуденновскВалдайВеликий НовгородВельскВладивостокВладикавказВладимирВолгоградВолгодонскВолжскийВологдаВолосовоВоркутаВоронежВыборгВышний ВолочекВязникиГеленджикГлазовГорно-АлтайскГрозныйГусь-ХрустальныйДальнегорскДербентДзержинскДмитровДомодедовоДонскойДубнаДушанбеЕкатеринбургЕлабугаЕлецЕлизовоЕреванЕссентукиЖелезногорскЗаречныйЗлатоустИвановоИжевскИрбитИркутскИшимЙошкар-ОлаКазаньКалининградКалугаКаменск-УральскКанскКарачаевскКаспийскКемеровоКерчьКиржачКировКирово-ЧепецкКисловодскКовровКольчугиноКомсомольск-на-АмуреКонаковоКопейскКоркиноКоряжмаКостромаКотласКрасноборскКраснодарКраснокаменскКрасноярскКудымкарКуйбышевКулебакиКумертауКунгурКурганКурскКызылЛениногорскЛесозаводскЛесосибирскЛикино-ДулёвоЛипецкЛугаЛысьваЛюберцыМагаданМагнитогорскМайкопМахачкалаМегионМиассМинскМихайловскМичуринскМончегорскМоршанскМоскваМурманскМуромМценскНабережные ЧелныНальчикНаро-фоминскНаходкаНевинномысскНерчинскНефтекамскНефтекумскНефтеюганскНижневартовскНижнекамскНижний НовгородНижний ТагилНиколаевск-на-АмуреНикологорыНовозыбковНовокузнецкНовомосковскНовороссийскНовосибирскНовочебоксарскНовый УренгойНорильскНоябрьскОбнинскОдинцовоОзерскОмскОрелОренбургОрскПензаПермьПетрозаводскПетропавловск-КамчатскийПетушкиПодольскПриозерскПрокопьевскПсковПущиноПятигорскРаменскоеРжевРостовРостов-на-ДонуРубцовскРыбинскРязаньс.
Пожалуйста, выберите, кем вы являетесьЯ абитуриентШкольник до 10 классаЯ родитель абитуриентаЯ учитель в школеЯ сотрудник вузаСтудент колледжаСпециалистБакалаврМагистр
Регистрируясь через данную форму, я соглашаюсь с политикой конфиденциальности и согласен на обработку персональных данных.
Хочу, что вы отправляли мне индивидуальные подборки и лучшие предложения от вузов по нужным мне критериям.
В.И. Арнольд, Об обучении математике
В.И. Арнольд, Об обучении математикеМатематика является частью физики. Физика — экспериментальная наука, часть естествознания. Математика — это та часть физики, где эксперименты обходятся дешево.
Тождество Якоби (которое заставляет высоты треугольника пересекаться на одной точка) является экспериментальным фактом, таким же, как то, что Земля круглая. (то есть гомеоморфны шару). Но его можно обнаружить с меньшими затратами. расход.
В середине ХХ века была предпринята попытка разделить физику
и математика. Последствия оказались катастрофическими.
Целые поколения математиков выросли, не зная и половины
своей науки и, конечно же,
при полном незнании каких-либо других наук.
Поскольку схоластическая математика, оторванная от физики, не годится ни ни для обучения, ни для применения в какой-либо другой науке, в результате всеобщая ненависть к математикам – как со стороны бедняков школьники (некоторые из которых тем временем стали министрами) и пользователей.
Уродливое здание, построенное малообразованными математиками
которые были измучены их
комплекса неполноценности и не сумевших свыкнуться с
физике, напоминает строгую аксиоматическую теорию нечетных чисел.
Очевидно, что создать такую теорию и заставить школьников восхищаться можно.
совершенство и внутреннюю согласованность получаемой структуры (в которой,
например, сумма нечетного числа слагаемых и произведение любого числа
факторов определены). С этой сектантской точки зрения даже
цифры могли быть либо объявлены ересью, либо со временем
введено в теорию
дополнены несколькими «идеальными» объектами (чтобы соблюсти
потребности физики и реального мира).
К сожалению, это была уродливая извращенная конструкция математики, подобная тот, который преобладал в преподавании математики на протяжении десятилетий. Возникнув во Франции, это извращение быстро распространилось на преподавание основ математика, сначала студентам университетов, затем школьникам всех линий (сначала во Франции, затем в других странах, в том числе и в России).
На вопрос “что такое 2+3″ француз ученик начальных классов ответил: «3+2, так как сложение коммутативно”. Он не знал, что сумма была равна и даже не мог понять о чем его спрашивают!
Другой французский ученик (вполне рациональный, на мой взгляд) определял математику как следует: «есть квадрат, но это еще нужно доказать».
Судя по моему преподавательскому опыту во Франции, представление студентов университета о
математике (даже из тех, кто преподавал математику в École Normale
Supérieure – мне больше всего жалко этих явно интеллигентных
но уродливые дети) так же беден, как и у этого ученика.
Например, эти студенты никогда не видели параболоид и вопрос о форма поверхности задается уравнением xy = z 2 ставит математиков, обучающихся в ENS, в ступор. Рисование кривой, заданной параметрические уравнения (типа x = t 3 – 3t, y = t 4 – 2т 2 ) на самолете есть совершенно неразрешимая задача для студентов (а, может быть, и для большинство французских профессоров математики).
Начиная с первого учебника л’Опиталя по математическому анализу («Исчисление для понимание кривых линий») и примерно до учебника Гурса, способность решать такие задачи считалась (наряду с знание таблицы умножения) необходимая часть ремесла каждого математик.
Умственно отсталые ревнители «абстрактной математики» бросили все
геометрия (через которую связь с физикой и реальностью чаще всего
имеет место в математике) вне преподавания.
Учебники по математическому анализу Гурса, Эрмита, Пикара недавно были выброшены на свалку.
студенческая библиотека университетов Париж 6 и 7 (Жюссье) как устаревшая
и, следовательно, вредные (их спасло только мое вмешательство).
Студенты ENS, прошедшие курсы по дифференциальным и алгебраическим геометрия (читается уважаемыми математиками) оказалась незнакомой ни с римановой поверхностью эллиптической кривой y 2 = х 3 + ax + b ни, собственно, с топологической классификацией поверхностей (не говоря уже об эллиптических интегралах первого рода и группе свойство эллиптической кривой, состоящее в том, что есть теорема сложения Эйлера-Абеля). Их учили только Ходжа структуры и многообразия Якоби!
Как такое могло случиться во Франции, подарившей миру Лагранжа и Лапласа,
Коши и Пуанкаре, Лерэ и Том? Мне кажется разумным
объяснение дал И.Г. Петровский,
который научил меня в 1966: настоящие математики делают
не группируются, но слабым нужны банды, чтобы выжить. Они могут объединиться на
различных мотивах (это может быть сверхабстрактность, антисемитизм или
“прикладные и производственные” проблемы), но суть всегда в решении
социальной проблемы – выживание в условиях более грамотного
окрестности.
Кстати, напомню предупреждение Л. Пастера: никогда не никаких “прикладных наук” не было и не будет, есть только приложений наук (весьма полезные!).
Я тогда с некоторым сомнением относился к словам Петровского, а теперь Я все больше и больше убеждаюсь в том, насколько он был прав. Значительная часть сверхабстрактная деятельность сводится просто к индустриализации бессовестных захват открытий у первооткрывателей, а затем систематическое присвоение их эпигонам-генерализаторам. Аналогично тому, что Америка не носят имя Колумба, математические результаты почти никогда не называются имена их первооткрывателей.
Во избежание неправильного цитирования, я должен отметить, что мои собственные достижения по какой-то неизвестной причине никогда не были экспроприированы таким образом, хотя это всегда случилось с обоими моими учителями (Колмогоровым, Петровским, Понтрягиным, Рохлиным) и мои ученики. Профессор М. Берри однажды сформулировал следующие два принципа:
Принцип Арнольда. Если понятие носит личное имя,
тогда это имя не имя первооткрывателя.
Если понятие носит личное имя,
тогда это имя не имя первооткрывателя.
Принцип Берри. Принцип Арнольда применим сам к себе.
Вернемся, однако, к преподаванию математики во Франции.
Когда я был студентом первого курса механико-математического факультета МГУ лекции по математическому анализу читал теоретико-множественный тополог Л.А. Тумаркин, добросовестно пересказавший старые курс классического исчисления французского типа в версии Гурса. Он сказал нам, что интегралы рациональных функций по алгебраической кривой можно взять, если соответствующее риманово поверхность есть сфера и, вообще говоря, не может быть взята, если ее род выше, а для сферичности достаточно иметь достаточно большое количество двойных точек на кривой заданной степени (что заставляет кривую быть уникурсальным: его реальные точки можно нарисовать на проективной плоскости одним росчерком пера).
Эти факты настолько захватывают воображение, что (даже приведенные без всякого
доказательства) они дают лучшее и более правильное представление о современной математике, чем
целые тома трактата Бурбаки. Действительно, здесь мы узнаем о
существование чудесной связи между вещами, которые кажутся полностью
отличается: с одной стороны, существованием явного выражения для
интегралы и топология
соответствующей римановой поверхности и, с другой стороны, между
число двойных точек и род соответствующей римановой поверхности, которые
также проявляет себя в реальной области как универсальность.
Действительно, здесь мы узнаем о
существование чудесной связи между вещами, которые кажутся полностью
отличается: с одной стороны, существованием явного выражения для
интегралы и топология
соответствующей римановой поверхности и, с другой стороны, между
число двойных точек и род соответствующей римановой поверхности, которые
также проявляет себя в реальной области как универсальность.
Якоби отметил, как наиболее увлекательное свойство математики, что в ней и одна и та же функция контролирует оба представления целого число как сумму четырех квадратов и реальное движение маятника.
Эти открытия связей между разнородными математических объектов можно сравнить с открытием связи между электричество и магнетизм в физике или с открытием сходства между восточным побережьем Америки и западным побережьем Африки в геологии.
Эмоциональное значение таких открытий для обучения трудно оценить.
переоценивать. Именно они учат нас искать и находить такие чудесные
явления гармонии Вселенной.
Дегеометризация математического образования и отрыв от физики разорвать эти связи. Например, не только студенты, но и современные алгебро-геометры в целом не знают о факте Якоби упоминается здесь: эллиптический интеграл первого рода выражает время движения по эллиптическая фазовая кривая в соответствующей гамильтоновой системе.
Перефразируя известные слова об электроне и атоме, можно сказать, что гипоциклоида неисчерпаема, как идеал в кольце многочленов. Но преподавать идеалы студентам, которые никогда не видели гипоциклоиды, нелепый как обучение сложению дробей детей, которые никогда не сокращали (по крайней мере, мысленно) торт или яблоко на равные части. Неудивительно, что дети предпочтут чтобы добавить числитель к числителю и знаменатель к знаменателю.
От моих французских друзей я слышал, что тенденция к сверхабстрактному
обобщения — их традиционная национальная черта. я не совсем
не согласен, что это
может быть, речь идет о наследственном заболевании, но я хотел бы подчеркнуть
тот факт, что я позаимствовал пример с пирогом и яблоком у Пуанкаре.
Схема построения математической теории и есть то же самое в любой другой естественной науке. Сначала мы рассматриваем некоторые объекты и делаем некоторые наблюдения в особых случаях. Затем мы пытаемся найти пределы заявление наших наблюдений, искать контрпримеры, которые помешали бы неоправданный расширение наших наблюдений на слишком широкий круг событий (пример: количество разделов последовательных нечетных чисел 1, 3, 5, 7, 9 на нечетное число натуральных слагаемых дает последовательность 1, 2, 4, 8, 16, но затем идет 29).
В результате мы формулируем сделанное нами эмпирическое открытие (например, гипотезу Ферма или гипотезу Пуанкаре) как можно яснее. После этого наступает трудный период проверки надежности являются выводы.
К этому моменту в математике была разработана специальная техника.
Этот прием в применении к реальному миру иногда бывает полезен, но может
иногда также приводят к самообману. Эта техника называется моделированием.
При построении модели делается следующая идеализация: определенные
факты, которые известны только с определенной долей вероятности или с
определенной степени точности, считаются «абсолютно»
правильны и принимаются как «аксиомы».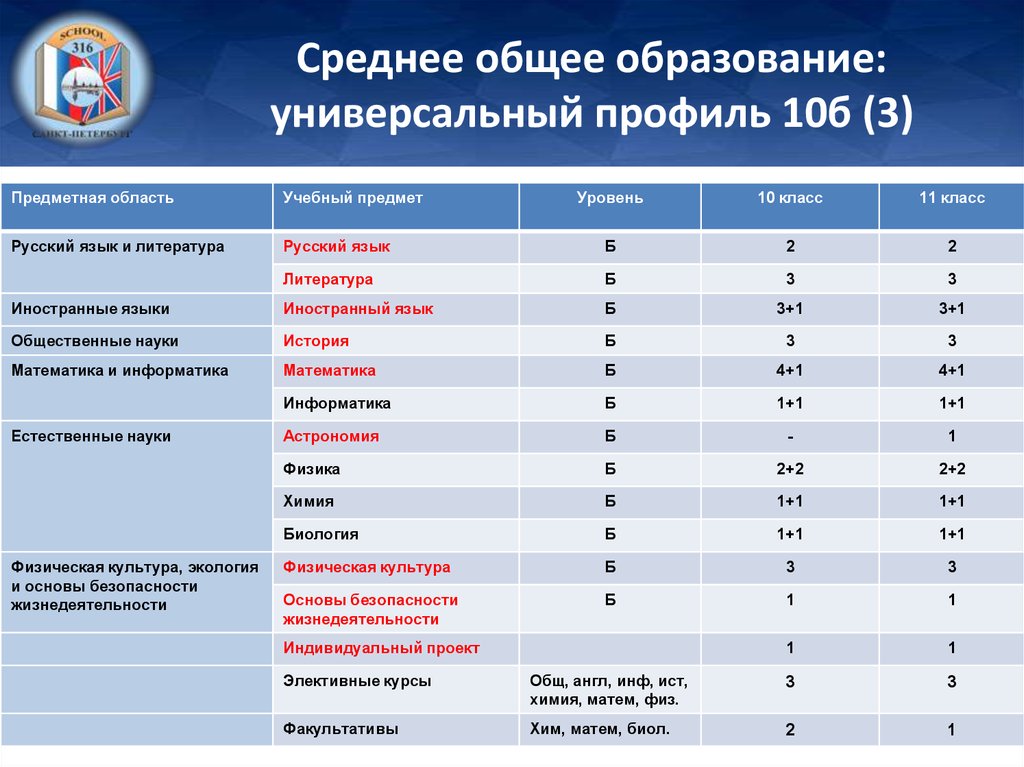 Смысл этой «абсолютности» именно в том, что
мы позволяем себе пользоваться этими «фактами» по правилам
формальной логики, при этом объявляя «теоремами» все, что
мы можем вывести из них.
Смысл этой «абсолютности» именно в том, что
мы позволяем себе пользоваться этими «фактами» по правилам
формальной логики, при этом объявляя «теоремами» все, что
мы можем вывести из них.
Очевидно, что ни в какой реальной деятельности невозможно полностью полагаться на такие выводы. Причина хотя бы в том, что параметры изученных явления никогда не известны абсолютно точно и небольшое изменение параметров (например, начальные условия процесса) могут полностью изменить результат. Скажем, по этой причине надежный долгосрочный прогноз погоды невозможно и останется невозможным, сколько бы мы ни развивали компьютеры и устройства, регистрирующие начальные условия.
Точно так же небольшое изменение в аксиомах (о которых мы не можем совершенно уверен) способен, вообще говоря, привести к совершенно выводы, отличные от тех, которые получаются из теорем, выводится из принятых аксиом. Чем длиннее и изящнее цепочка выводов («доказательств»), тем менее надежен конечный результат.
Сложные модели редко бывают полезны (если только те, кто пишет свои
диссертации).
Математическая техника моделирования состоит в игнорировании этой проблемы и говоря о своей дедуктивной модели так, как будто она совпала с реальностью. Тот факт, что этот путь, заведомо неверный с точки зрения естествознания, часто приводит к полезным результатам в физике. назвал «невообразимой эффективностью математики в естественных науках». (или «принцип Вигнера»).
Здесь можно добавить замечание И.М. Гельфанда: существует еще другое явление, сравнимое по своей немыслимости с невероятная эффективность математики в физике, отмеченной Вигнером, – это в равной степени немыслимая неэффективность математики в биологии.
«Тонкий яд математического образования» (по выражению Ф. Клейна) для
физики состоит именно в том, что
абсолютизированная модель отделяется от
реальность и уже не сравнивается с ней. Вот простой пример:
математика
учит нас, что решение уравнения Мальтуса dx/dt = x однозначно
определяется начальными условиями (т. е. соответствующим интегралом
кривые в (t,x)-плоскости не пересекаются). Этот вывод
математическая модель имеет мало отношения к реальности. Компьютер
Эксперимент показывает, что все эти интегральные кривые имеют общие точки на
отрицательная полуось t. Действительно, скажем, кривые с начальным
условия x(0) = 0 и x(0) = 1 практически пересекаются при t = -10 и
при t = -100 вы не можете вместить атом между ними. Свойства пространства при таких малых
расстояния вообще не описываются евклидовой геометрией. Применение
теорема единственности в этой ситуации явно превосходит точность
модель. Это необходимо учитывать при практическом применении модели.
иначе можно столкнуться с серьезными неприятностями.
Этот вывод
математическая модель имеет мало отношения к реальности. Компьютер
Эксперимент показывает, что все эти интегральные кривые имеют общие точки на
отрицательная полуось t. Действительно, скажем, кривые с начальным
условия x(0) = 0 и x(0) = 1 практически пересекаются при t = -10 и
при t = -100 вы не можете вместить атом между ними. Свойства пространства при таких малых
расстояния вообще не описываются евклидовой геометрией. Применение
теорема единственности в этой ситуации явно превосходит точность
модель. Это необходимо учитывать при практическом применении модели.
иначе можно столкнуться с серьезными неприятностями.
Замечу, однако, что та же теорема единственности объясняет, почему
завершающий этап швартовки судна к причалу осуществляется вручную:
на рулевом управлении, если бы скорость подхода была определена
как гладкая (линейная) функция расстояния, процесс швартовки будет
потребовалось бесконечно много времени. Альтернатива – воздействие
с причалом (демпфируемым подходящими неидеально упругими телами).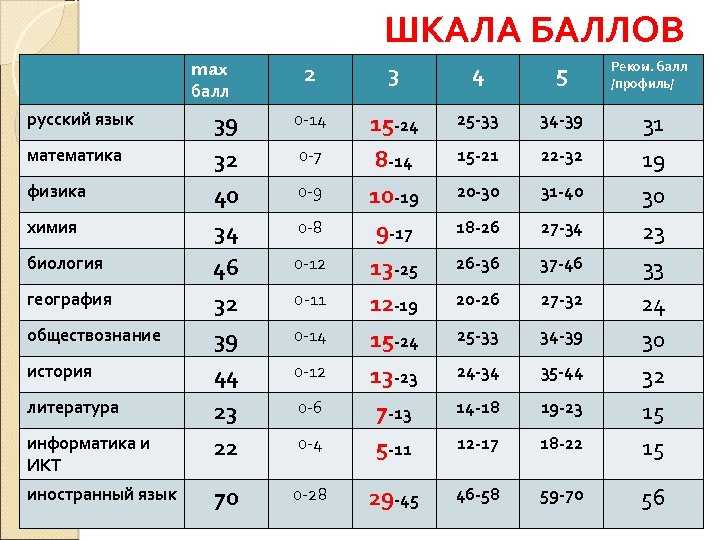 Посредством
Кстати, с этой проблемой пришлось серьезно столкнуться при посадке первого
спускаемых аппаратов на Луну и Марс, а также на стыковку с космосом
станции – тут против нас работает теорема единственности.
Посредством
Кстати, с этой проблемой пришлось серьезно столкнуться при посадке первого
спускаемых аппаратов на Луну и Марс, а также на стыковку с космосом
станции – тут против нас работает теорема единственности.
К сожалению, ни такие примеры, ни обсуждение опасности Теоремы фетишизации можно встретить в современных математических учебниках, даже в лучшие. У меня даже сложилось впечатление, что схоластические математики (кто мало знаком с физикой) верят в принципиальную разницу принадлежащий аксиоматическая математика из моделирования, которое распространено в естествознании и что всегда требует последующего контроля выводов экспериментом.
Не говоря уже об относительности исходных аксиом, нельзя
забыть о неизбежности логических ошибок в длинных рассуждениях (скажем, в
форма поломки компьютера, вызванная космическими лучами или квантовыми
колебания). Каждый работающий математик знает, что если не контролировать
себя (лучше всего на примерах), то через каких-нибудь десять страниц половина всего
знаки в формулах будут неверными и двойки найдут дорогу
из знаменателей в числители.
Технология борьбы с такими ошибками – это тот же внешний контроль путем эксперименты или наблюдения, как и в любой экспериментальной науке, и это должно быть учат с самого начала всех младших школьников.
Попытки создания «чистой» дедуктивно-аксиоматической математики привели к
отказ от схемы, используемой в физике
(наблюдение – модель – исследование модели –
выводы – проверка наблюдениями) и его подстановка по схеме:
определение – теорема – доказательство. Немотивированного понять невозможно.
определения, но это не останавливает преступных алгебраистов-аксиоматизаторов.
Например, они без труда определили бы произведение натуральных чисел
с помощью правила длинного умножения.
При этом коммутативность умножения становится трудно проверить.
доказать, но все еще возможно вывести его как теорему из аксиом.
Тогда можно заставить бедных студентов выучить эту теорему и ее доказательство.
(с целью повышения авторитета как науки, так и
лица, обучающие этому). Очевидно, что такие определения и
такие доказательства могут только навредить обучению и практической работе.
Понять коммутативность умножения можно только на подсчет и пересчет солдат по чинам и шеренгам или путем подсчета площадь прямоугольника двумя способами. Любая попытка обойтись без этого вмешательства физикой и действительностью в математику есть сектантство и изоляционизм, которые разрушить образ математики как полезной человеческой деятельности в глазах все здравомыслящие люди.
Открою еще несколько таких секретов (в интересах бедных студентов).
Определитель матрицы представляет собой (ориентированный) объем матрицы. параллелепипед, ребра которого являются его столбцами. Если учащимся сказать об этом секрет (который тщательно спрятан в очищенном алгебраическом образовании), тогда вся теория детерминантов становится ясной главой теория полилинейных форм. Если определители определены иначе, то любой здравомыслящий человек будет вечно ненавидеть все детерминанты, якобианцев и теорема о неявной функции.
Что такое группа ? Алгебраисты учат, что это якобы множество с
две операции, которые удовлетворяют множеству легко забываемых аксиом.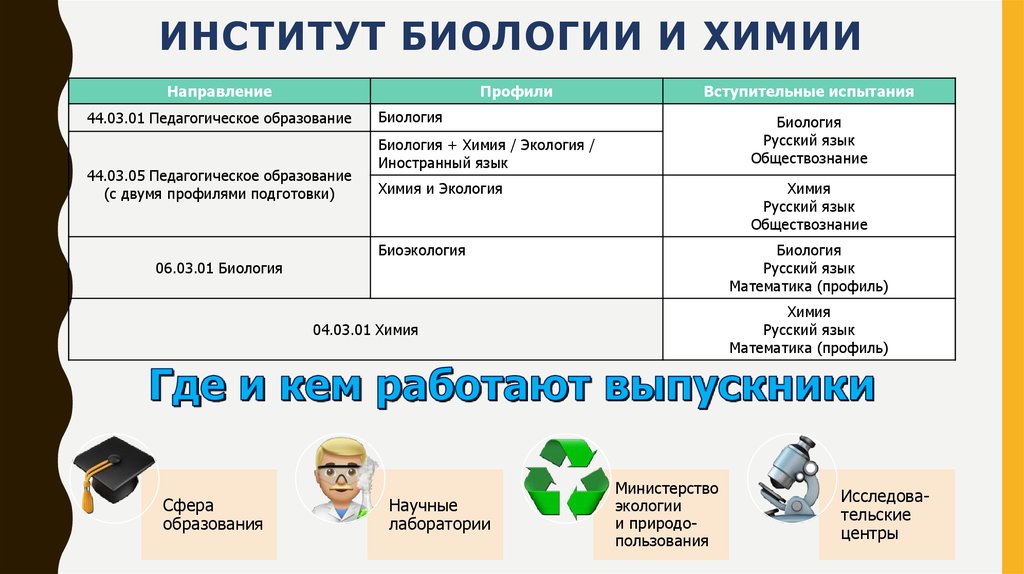 Этот
определение вызывает закономерный протест: зачем здравомыслящему человеку такие
пары операций? “О, будь проклята эта математика”
– заключает студент (который, возможно, станет министром науки в
будущее).
Этот
определение вызывает закономерный протест: зачем здравомыслящему человеку такие
пары операций? “О, будь проклята эта математика”
– заключает студент (который, возможно, станет министром науки в
будущее).
Мы получим совершенно другую ситуацию, если начнем не с группы. но с понятием преобразования (однозначное отображение множества на себя) как это было исторически. Совокупность преобразований множества называется группой, если наряду с любыми двумя преобразованиями она содержит результат их последовательного применения и обратного преобразования вместе с каждым преобразованием.
Вот и все определения. Так называемые «аксиомы» на самом деле
всего (очевидных) свойств групп преобразований.
Какие аксиоматизаторы
называть «абстрактными группами» — это всего лишь группы преобразований различных множеств
рассматриваются с точностью до изоморфизмов (которые являются взаимно однозначными отображениями
сохранение операций). Как доказал Кейли, нет «более абстрактных»
группы в мире.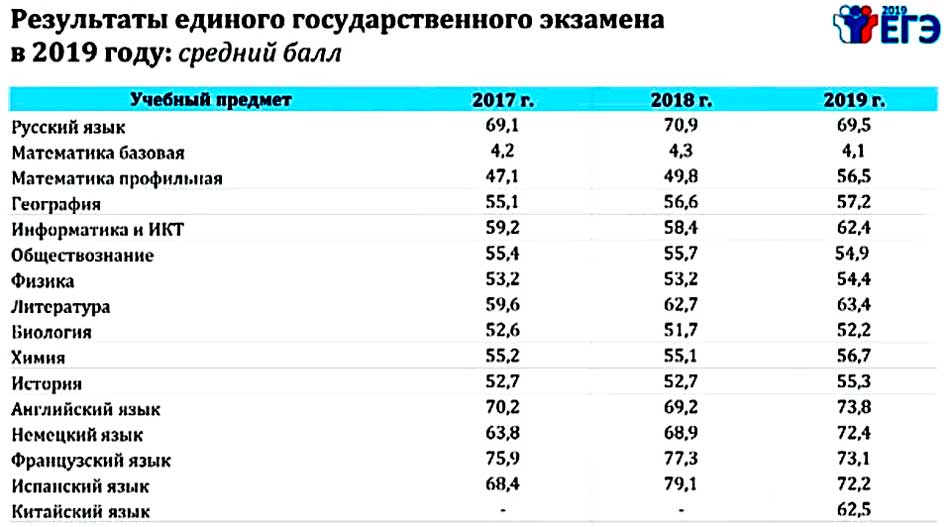 Так почему же алгебраисты продолжают мучить студентов
с абстрактным определением?
Так почему же алгебраисты продолжают мучить студентов
с абстрактным определением?
Кстати, в 1960-е годы я преподавал в Москве теорию групп. школьников . Избегая всей аксиоматики и оставаясь как можно ближе возможной физике, за полгода я добрался до теоремы Абеля о неразрешимость общего уравнения пятой степени в радикалах (имеющего попутно учили школьников комплексным числам, римановым поверхностям, фундаментальным группы и группы монодромии алгебраических функций). Этот курс был позже издано одним из слушателей, В. Алексеевым, как книга Теорема Абеля в задачах .
Что такое гладкий коллектор ? В недавней американской книге я прочитал, что Пуанкаре не был знаком с этим (представлено им самим) понятие и что «современное» определение было дано Вебленом только в конце 1920-х годов: многообразие — это топологическое пространство, удовлетворяющее длинному ряду аксиом.
За какие грехи студенты должны пытаться найти выход из всех этих поворотов
и повороты? На самом деле, в анализе Пуанкаре Location есть
абсолютно
четкое определение гладкого многообразия, которое гораздо полезнее, чем
«абстрактный».
Гладкое k-мерное подмногообразие евклидова пространства R N это его подмножество, которое в окрестности каждой своей точки является графом гладкой преобразование R k в R (N – k) (где R k и R (N – k) координаты подпространства). Это прямое обобщение большинства обыкновенный гладкий кривых на плоскости (скажем, круга x 2 + y 2 = 1) или кривые и поверхности в трехмерном пространстве.
Между гладкими многообразиями естественным образом определяются гладкие отображения. Диффеоморфизмы — это отображения, которые являются гладкими вместе со своими обратными.
«Абстрактное» гладкое многообразие — это гладкое подмногообразие евклидова пространства. рассматривается с точностью до диффеоморфизма. Нет “более абстрактных” конечномерные гладкие многообразия в мире (теорема Уитни). Почему мы продолжаем мучать студентов абстрактным определением? Не лучше ли было бы доказать их теорема о явной классификации замкнутых двумерных многообразия (поверхности)?
Именно эта замечательная теорема (утверждающая, например, что любое компактное
связная ориентированная поверхность представляет собой сферу с множеством ручек), что дает
правильное представление о том, что такое современная математика, а не
сверхабстрактный
обобщения наивных подмногообразий евклидова пространства, которые на самом деле
не дают ничего нового и преподносятся как достижения
аксиоматизаторы.
Теорема классификации поверхностей — первоклассная математическая достижение, сравнимое с открытием Америки или рентгеновских лучей. Это подлинное открытие математического естествознания и является даже сложно сказать относится ли сам факт больше к физике или к математике. В его значение как для приложений, так и для разработки правильных Weltanschauung намного превосходит такие «достижения» математика как доказательство последней теоремы Ферма или доказательство факта что любое достаточно большое целое число можно представить в виде суммы трех простые числа.
Ради рекламы современные математики иногда представлять такие спортивные достижения как последнее слово в своей науке. Понятно, что это не только не способствует пониманию обществом математики но на напротив, вызывает здоровое недоверие к необходимости тратить энергию на (скалолазные) упражнения с этими экзотическими вопросами никому не нужен и не нужен.
Теорема о классификации поверхностей должна была быть включена в высокий
школьные курсы математики (наверное, без пруфов), но почему-то
не входит даже в университетские курсы математики (из которых во Франции,
кстати, вся геометрия была изгнана за последние несколько десятилетий).
Возвращение преподавания математики на всех уровнях от схоластической болтовни к представлению важной области естествознание – особенно горячая проблема для Франции. Я был поражен тем, что все лучшее и самое важное в методический подход математические книги здесь почти неизвестны студентам (и, как мне кажется, не переведены на французский язык). Среди них Числа и цифры Радемахера и Тёпица, Геометрия и воображение Гильберта и Кон-Фоссена, Что такое математика? Курант и Роббинс, Как решить и Математика и правдоподобные рассуждения Поля, Развитие математика в 19 веке Ф. Кляйн.
Я хорошо помню, какое сильное впечатление произвел курс исчисления Эрмита. (который есть в русском переводе!) сделанный на меня в школьные годы.
В ней появились римановы поверхности, кажется, в одной из первых лекций (все
анализ был, конечно, комплексный, как и должно быть). Асимптотика
интегралы исследовались с помощью траекторных деформаций на римановых
поверхности при движении точек ветвления (сегодня мы назвали бы
это теория Пикара-Лефшеца; Пикард, между прочим, принадлежал Эрмиту. зять – математические способности часто передаются
зятья: династия Адамара – П. Леви – Л. Шварц – У. Фриш – это
еще один известный пример в Парижской академии наук).
зять – математические способности часто передаются
зятья: династия Адамара – П. Леви – Л. Шварц – У. Фриш – это
еще один известный пример в Парижской академии наук).
«Устаревший» курс Эрмита столетней давности (вероятно, сейчас выброшены из студенческих библиотек французских университетов) был намного современнее тех самых занудных исчислений учебники, с которыми нынче мучают школьников.
Если математики не одумаются, затем потребители, которые сохранили потребность в современном, в лучшем смысле этого слова, математическая теория, а также как иммунитет (свойственный любому здравомыслящий человек) к бесполезной аксиоматической болтовне в конце концов откажется от услуг малообразованных схоластов как в школах, так и в университетах.
Учитель математики, не разобравшийся хотя бы с некоторыми томов курса Ландау и Лифшица, станет тогда реликт, как тот, что в наши дни, кто не знает разницы между открытым и закрытым множеством.
В.И. Арнольд
Перевод А. В. ГОРЮНОВ
В. ГОРЮНОВ
Опубликовано в: Успехи мат. наук 53 (1998), вып. 1, 229-234;
Английский перевод: русский мат. Опросы 53 (1998), нет. 1, 229-236.
Источник этого текста:
http://www.ceremade.dauphine.fr/~msfr/articles/arnold/PRE_anglais.ps
Ресурсы по математике и мероприятия для учащихся с ограниченными возможностями
Вовлечение и интерес учащихся к математике имеет решающее значение для того, чтобы помочь им сосредоточиться на задании и добиться успешных результатов. Для этого требуется не только изменить образ мышления, но и бросить вызов существующим стереотипам о том, как учатся учащиеся с ограниченными возможностями (SWD) и что они могут делать на уроках математики. Это также требует достойного отношения к учащимся-инвалидам в связи с присущими им способностями мыслить и заниматься математикой. Ниже приведен набор ресурсов, которые педагоги, семьи и лица, осуществляющие уход, могут использовать при обучении и поддержке всех учащихся.
Найдите задания, материалы и ресурсы, связанные с математикой, с которыми будут работать ваши ученики, изучив коллекцию ресурсов ниже.
Обратите внимание, что приведенные ссылки являются рекомендациями по ресурсам и не означают поддержку или одобрение Департаментом образования штата Нью-Джерси каких-либо продуктов, услуг или мнений корпорации, организации или отдельных лиц.
- Ранняя математика. Что нужно знать и делать, чтобы помочь дошкольнику изучить математику?
- Помогите своему ребенку развить навыки математики в раннем возрасте. Узнайте, какие неформальные занятия дают детям преимущество, когда они начинают изучать математику в школе.
- НАЭЙЦ | Математика – увлекательные статьи по изучению математики.
- «Улица Сезам» в сообществах — Главная — Сотни двуязычных мультимедийных инструментов, помогающих детям и семьям обогатить и расширить свои знания в период от рождения до шести лет, что является критическим периодом для развития мозга. Наши ресурсы вовлекают детей и взрослых в повседневные моменты и повседневные дела — от обучения детей математике и грамотности до обучения семей правильному питанию и до серьезных тем, таких как развод и отсутствие продовольственной безопасности.

- Краткий обзор практического руководства по обучению математике детей младшего возраста: Краткое изложение практического руководства для педагогов – опирайтесь на естественный интерес детей к математике, чтобы сделать дошкольные учреждения более увлекательными и полезными.
- 99Математика – простой и увлекательный способ попрактиковаться в математических фактах в классе! Привлекательный и идеально подходит для всех видов деятельности. Учетные записи студентов не требуются.
- AAA Math – содержит полный набор интерактивных уроков по арифметике. Практика доступна по каждой теме, что позволяет полностью овладеть концепциями. Вы можете сортировать по уровню обучения. К-8.
- Брейн-поп | Математика – группа образовательных веб-сайтов с более чем 1000 короткометражными анимационными фильмами для учащихся классов K–12, а также викторинами и соответствующими материалами по естественным наукам, общественным наукам, английскому языку, математике, технике и технологиям, здравоохранению и искусству.
 музыка
музыка - Cabin Fever Math — Математика перед сном — Математика перед сном помогает семьям превратить математику в забавную часть своей повседневной жизни, например любимую сказку на ночь.
- Геогебра | Elementary – изучите более 300 ресурсов, с помощью которых учащиеся начальной школы могут изучать математические понятия в увлекательной и интерактивной форме!
- I Know It – сайт для занятий математикой для детей – комплексный интерактивный сайт для занятий по математике для учащихся от детского сада до пятого класса.
- Investigations Math Games – двуязычные математические игры, основанные на исследованиях.
- Игра «Монстры против фракций» от SMART | Monsters vs Fractions – забавный сайт, который использует игровое обучение, чтобы «разгадать» загадку и изучить дроби.
- NRICH — Математический проект NRICH (на базе Кембриджского университета) предлагает математические ресурсы для детей, родителей и учителей, чтобы обогатить обучение.
 Он предоставляет ресурсы для студентов всех возрастов.
Он предоставляет ресурсы для студентов всех возрастов. - PhET: бесплатные онлайн-симуляции по физике, химии, биологии, наукам о Земле и математике – бесплатные симуляции K-12 по естествознанию и математике для обучения темам STEM, включая физику, химию, биологию и математику, от Университета Колорадо в Боулдере.
- SplashLearn – программа обучения, ориентированная на учебную программу, которая охватывает математические навыки K-5 с помощью увлекательных игр.
- Виртуальные манипуляции для математики | Didax – виртуальные манипуляторы – отличный способ улучшить домашнее обучение. Просто перетащите манипуляторы в нужное положение, чтобы увидеть, как математические концепции оживают!
- Zearn Math – учебная программа K-5 направлена на формирование у всех учащихся глубокого понимания и любви к изучению математики.
- Несмотря ни на что: внутренняя статистика — показывает учащимся актуальность статистики в реальных условиях. Серия видеороликов для школьников и студентов.

- Covid-19: закрытие школ – бесплатная поддержка, ресурсы и идеи по математике – готовые к использованию ресурсы для MS/HS по математике.
- Геогебра | Старшая школа. Изучите более 1700 ресурсов, с помощью которых учащиеся старших классов могут изучать математические понятия в увлекательной и интерактивной форме!
- Геогебра | Средняя школа. Изучите более 500 интерактивных ресурсов, с помощью которых учащиеся средней школы могут изучать математические понятия в увлекательной игровой форме!
- Математика в основе: средняя школа от PBS Learning — найдите увлекательные, основанные на стандартах средства массовой информации и комплексные занятия.
- Головоломки SolveMe. Используйте логику для решения визуальных интерактивных математических головоломок.
- PhET: бесплатные онлайн-симуляции по физике, химии, биологии, наукам о Земле и математике – бесплатные симуляции K-12 по естествознанию и математике для обучения темам STEM, включая физику, химию, биологию и математику, от Университета Колорадо в Боулдере.

- Виртуальный ботаник – более 1500 видеоуроков от математики для средних классов до алгебры 2
- Yummy Math – математика в реальном мире – увлекательные математические задания в реальном мире.
- Перепись | Статистика в школе. Используйте реальную статистику Бюро переписи населения для создания материалов, которые можно использовать год за годом во всех классах.
- Desmos – коллекция бесплатных цифровых заданий по математике для учителей и учащихся.
- Expii. Исследуйте ежедневные задачи, уроки и интерактивные математические головоломки для предварительной алгебры, алгебры 1 и биологии.
- Курс финансовой алгебры | NGPF – бесплатная учебная программа для учителей математики в старших классах, которые хотят создавать приложения для личных финансов в реальном мире с согласованием математических стандартов и глубокой алгебраической строгостью.
- Бесплатные ресурсы для онлайн-обучения математике | NCTM – Поскольку в настоящее время так много учителей переходят на онлайн-обучение, NCTM предлагает эти бесплатные ресурсы для поддержки учителей и их учеников.

- Графические органайзеры для помощи детям в математике | Понял.org
- Исследовательская математика. Исследовательская математика — это модель обучения, которая побуждает учащихся регулировать свою деятельность при изучении математического утверждения.
- Изучение COVID-19 с помощью математики
- Обучающие видеоролики по математике – тысячи бесплатных обучающих видеоклипов по всем предметам для учителей, учащихся и родителей.
- Центр обучения математике | Бесплатные уроки и публикации – инновационная и основанная на стандартах учебная программа, ресурсы и профессиональное развитие.
- Планы уроков математики | Teacher.org – Уроки от начальной до средней школы, организованные по классам, создаются учителями из школ США.
- Национальная библиотека виртуальных манипуляций – Концептуальные задания по числам и операциям, алгебре, геометрии, измерениям, анализу данных и уровням вероятности PreK-12.
- Open Middle® — Сложные математические задачи, которые стоит решить — Поставьте перед учащимися задачу решить математические задачи с «открытой серединой» и несколькими способами решения задачи.

- Реальный мир | NASA eClips Real World – ресурсы, связывающие школьную математику с карьерой и инновациями 21 века.
- Summer Math Challenge — это бесплатная шестинедельная программа, которая помогает учащимся практиковать математические навыки, полученные в течение учебного года. Когда вы присоединитесь к соревнованию, вы получите доступ к ежедневным увлекательным занятиям и ресурсам, разработанным для вашего класса и уровня способностей вашего ученика.
- UDL Tech Toolkit — математические инструменты — онлайн-математические инструменты и визуальные манипуляторы делают обучение доступным для всех учащихся.
- Какой из них не принадлежит? – Предоставляет наводящие на размышления головоломки для учителей математики и студентов.
- XtraMath — некоммерческая организация 501(c)(3), занимающаяся математическими достижениями для всех. Наша цель — разработать эффективные, действенные, адаптивные и внутренне полезные дополнительные математические занятия.

- Youcubed – некоммерческая организация, предлагающая бесплатные ресурсы по математике для школьников и семей для школьников и родителей.
Поддержка сетей распознавания
- Определение математической лексики, символов и обозначений с помощью математических словарей
- Проиллюстрируйте ключевые понятия с помощью различных представлений, включая слова, символы, графики, диаграммы, таблицы, формулы и манипуляции (физические или онлайн).
- Предоставить или активировать базовые знания; Соедините новые знания с ранее изученными понятиями посредством обсуждений; написание подсказок и рассуждений.
- См. практическое руководство USDOE и дополнительные примеры
Поддержка стратегических сетей
- Разнообразные способы взаимодействия и реагирования
- Содействовать управлению информацией и ресурсами; примеры
- Предоставление строительных лесов для тренировок и выступлений; примеры
- Расширение возможностей для мониторинга прогресса
- Предоставить соответствующие инструменты, такие как Microsoft math и Wolfram alpha
Поддержка аффективных сетей
- Предлагайте варианты, из которых учащиеся могут выбирать.
 Примеры и инструкции
Примеры и инструкции - Различные уровни вызовов и поддержки
- Повышение обратной связи, ориентированной на мастерство
- Повышение актуальности, ценности и подлинности; Уменьшите угрозы, отвлекающие факторы.
- Предоставление возможностей для саморегулирования. Полезные советы и способы борьбы со стрессом
Нажмите здесь, чтобы узнать больше об универсальном дизайне для обучения (NJDOE)
- Помощь учащимся, испытывающим затруднения с математикой: Response to Intervention (RtI) для начальных и средних школ. Это руководство предназначено для учителей, директоров и администраторов, чтобы помочь учителям, директорам и администраторам использовать Response to Intervention для раннего выявления, предотвращения и поддержки учащихся, испытывающих трудности с математикой. .
- Энциклопедия Best Evidence — Математика для средних и старших классов — в этом обзоре обобщаются данные о трех типах программ, разработанных для улучшения успеваемости учащихся 6–12 классов по математике.

- Учебный центр – коллекция научно-исследовательских ресурсов по обучению. Хотя эти ресурсы полезны для улучшения успеваемости всех учащихся, они в первую очередь предназначены для учащихся школ с самой низкой успеваемостью, учащихся с трудностями в изучении математики, учащихся, нуждающихся в интенсивном обучении, или учащихся с особыми потребностями/разнообразных учащихся, включая изучающих английский язык.
- Инструкция по построению эффективных дробей для детей от детского сада до 8-го класса | WWC – В этом практическом руководстве представлены пять рекомендаций, призванных помочь преподавателям улучшить понимание учащимися дробей.
- Inside Mathematics – профессиональный ресурс для учителей, тренеров и администраторов, увлеченных улучшением обучения и успеваемости учащихся по математике.
- Illuminations (NCTM) – планы уроков, задания, игры и головоломки от NCTM. Фильтруйте по типу ресурса, уровню обучения (PreK-12) или стандартам.
- Ресурсы для обучения математике K-5 — ресурсы для обучения математике K-5 и возможности профессионального обучения для поддержки совершенства и преобразования преподавания и изучения математики, улучшения результатов для всех учащихся в начальной школе и за ее пределами.

- Центр математики Кентукки Серия вебинаров – бесплатные онлайн-мини-классы для преподавателей.
- Инструкция по математике для учащихся с ограниченными возможностями обучения или с трудностями в обучении. Этот документ служит руководством для учителей K–12 учащихся с ограниченными возможностями и учащихся из групп риска при выборе и использовании эффективных методов обучения математике.
- Математические интервенции | Education Northwest – Математические вмешательства: какие стратегии помогают учащимся, испытывающим затруднения, или учащимся с ограниченными возможностями обучения? Исследования и ресурсы, которые могут помочь учителям математики использовать надежные методы обучения.
- Национальный центр интенсивного вмешательства – Математика – NCII разработал серию уроков по математике и руководств для поддержки преподавателей специального образования, специалистов по математике и других лиц, работающих с учащимися, испытывающими трудности с математикой.

- Национальный совет учителей математики. Математический форум имеет богатую историю как онлайн-центр для сообщества математического образования. NCTM делает многие из самых популярных частей контента Math Forum доступными для сообщества математического образования.
- Национальная библиотека виртуальных манипуляций – Концептуальные задания по числам и операциям, алгебре, геометрии, измерениям, анализу данных и уровням вероятности PreK-12.
- 100 дней профессионального развития NCTM – 60-минутные вебинары, представленные избранными докладчиками из программы ежегодных встреч и выставок NCTM Centennial Meeting & Exposition.
- Skew The Script – предлагает бесплатные социально значимые уроки математики по алгебре 1, алгебре 2 и AP. изменение климата, вопросы справедливости, контроль над оружием и прививки.
- Стратегии обучения для улучшения знаний по алгебре учащихся средних и старших классов | WWC – это практическое руководство содержит три рекомендации по обучению алгебре учащихся средних и старших классов.

