| Направление подготовки / Специальность / Образовательная программа | Бюджетных мест / вкл. квоту |
Платных мест |
Проходной балл (бюджет) в 2020 г. 1 волна / 2 волна |
Вступительные испытания в 2021 г. |
|
|---|---|---|---|---|---|
| 05.03.02 |
География Программа: География Форма обучения: Очная Уровень: Бакалавр |
74 / 8 |
28 |
325 / 311 |
|
05. 03.04 03.04 |
Гидрометеорология Программа: Гидрометеорология Форма обучения: Очная Уровень: Бакалавр |
24 / 3 |
10 |
307 / 299 |
|
| 05.03.03 |
Картография и геоинформатика Программа: Картография и геоинформатика Форма обучения: Очная Уровень: Бакалавр |
14 / 2 |
5 |
339 / 340 |
|
43. 03.02 03.02 |
Туризм Программа: Туризм Форма обучения: Очная Уровень: Бакалавр |
10 |
|
||
| 43.03.02 |
Туризм Программа: Туризм и рекреация Форма обучения: Очная Уровень: Бакалавр |
10 |
|
||
05. 03.06 03.06 |
Программа: Экология и природопользование Форма обучения: Очная Уровень: Бакалавр |
34 / 4 |
12 |
313 / 303 |
|
Минпросвещения опубликовало проект расписания ЕГЭ на 2021 год :: Общество :: РБК
ЕГЭ планируется начать 31 мая, а ОГЭ — 24 мая. В этот же день начнется упрощенный экзамен, которым можно заменить сдачу единого госэкзамена, — ГВЭ
В этот же день начнется упрощенный экзамен, которым можно заменить сдачу единого госэкзамена, — ГВЭ
Фото: Михаил Терещенко / ТАСС
Минпросвещения предложило утвердить расписание ЕГЭ на 2021 год, проект приказа опубликован на портале нормативных актов.
Если документ будет одобрен, ЕГЭ в этом году начнется 31 мая и завершится 2 июля, дополнительные экзамены пройдут с 12 по 17 июля.
Согласно расписанию, первыми экзаменами будут география, литература и химия. За ними школьники будут сдавать русский язык, его предлагается разбить на два дня (3 и 4 июня). В течение трех дней будут проходить экзамены по иностранному языку: 18 июня учащиеся будут сдавать основной массив экзамена, а 21 и 22 июня зарезервировали для устной части, раздела «Говорение». Также на два дня предлагается разбить сдачу информатики.
Полное расписание:
31 мая — география, литература и химия;
3 июня — русский язык;
4 июня — русский язык;
7 июня — профильная математика;
11 июня — история, физика;
15 июня — обществознание;
18 июня — биология, иностранный письменно;
21 июня — иностранный язык, устная часть;
22 июня — иностранный язык, устная часть;
24 июня — информатика, ИКТ;
25 июня — информатика, ИКТ;
28, 29 июня, 2 июля — резервные дни.
Министерство также опубликовало проекты расписаний основного государственного экзамена (ОГЭ), который сдают девятиклассники, и государственного выпускного экзамена (ГВЭ-9), упрощенного экзамена, который заменяет ЕГЭ для тех выпускников, которые не планируют поступать в вузы.
Три причины сдавать ЕГЭ по профильной математике — Российская газета
1 февраля заканчивается срок подачи заявлений на ЕГЭ. Никаких изменений по датам на этот счет пока не объявлено, так что просчитываем варианты поступления в вузы и обращаем самое пристальное внимание на… ЕГЭ по профильной математике.
Три причины выбрать ЕГЭ по математике
Первая. ЕГЭ по профильной математике на очень большом количестве вузовских специальностей и направлений – в числе однозначно обязательных для всех вузов, как и ЕГЭ по русскому языку (а вот с третьим экзаменом ситуация другая. О ней расскажем ниже). Каких больших групп направлений подготовки это касается? “Математика, информационные науки и технологии”, “машиностроение, автоматизация и робототехника”, “энергетика и электротехника”, а также касается специальностей, связанных с транспортом, строительством, экономикой. К слову, именно на эти направления выделено самое большое количество бюджетных мест.
Вторая. Представьте себе, на таких вроде бы нематематических направлениях, как “промышленное рыболовство”, “ландшафтная архитектура”, “управление персоналом”, “реконструкция и реставрация архитектурного наследия” и даже “сервис” (!) от абитуриента в вузах потребуют ЕГЭ по математике.
Представьте себе, на таких вроде бы нематематических направлениях, как “промышленное рыболовство”, “ландшафтная архитектура”, “управление персоналом”, “реконструкция и реставрация архитектурного наследия” и даже “сервис” (!) от абитуриента в вузах потребуют ЕГЭ по математике.
Третья. Есть специальности, где ЕГЭ по математике не является обязательным абсолютно для всех вузов, НО (!) учебное заведение теперь имеет право добавить математику в качестве третьего экзамена из списка предложенных. Например, вы собираетесь поступать на “психологию” – популярное, перспективное направление, которое есть во многих вузах. Два ЕГЭ обязательны на “психологии” абсолютно для всех вузов. Это ЕГЭ по русскому языку и биологии, а вот третьим экзаменом может быть обществознание, иностранный язык или… математика. В Санкт-Петербургском госуниверситете, например, на “психологии” от вас попросят именно ЕГЭ по математике (плюс русский и биология). А вот в Южно-Уральском государственном гуманитарно-педагогическом университете абитуриентам вместо математики нужно будет принести ЕГЭ по обществознанию.
Хотите быть режиссером или продюсером? Готовьтесь, что будут вузы, которые потребуют не только ЕГЭ по русскому и литературе, но, возможно, и по профильной математике. Неожиданно? Но дела обстоят именно так. Как узнать, какие ЕГЭ нужны вузам на ваших специальностях? Самый надежный способ – зайти самому на сайт выбранного вуза и изучить список экзаменов. Советуем поторопиться, до 1 февраля не так уж далеко.
PS. Если уж совсем дела с математикой обстоят туго, сдавайте ЕГЭ по информатике. Информатику в качестве третьего предмета тоже наверняка будут спрашивать на многих специальностях.
| ДАТА | ЕГЭ | ГВЭ | РЕЗУЛЬТАТЫ (не позднее) |
||
|---|---|---|---|---|---|
|
25.05.2021
|
Русский язык | Продолжительность: 3 часа 55 минут (новая категория участников (для аттестата) — 2 часа 30 минут) |
04. 06.2021 06.2021 |
||
|
28.05.2021
|
Математика | Продолжительность: 3 часа 55 минут (новая категория участников (для аттестата) — 2 часа) |
04.06.2021 | ||
|
31.05.2021
|
Литература | Продолжительность: 3 часа 55 минут Минимальные баллы: 32 |
15.06.2021 | ||
| Химия | Продолжительность: 3 часа 30 минут Минимальные баллы: 36 |
||||
| География | Продолжительность: 3 часа Минимальные баллы: 37 |
||||
03. 06.2021 06.2021
|
Русский язык | Продолжительность: 3 часа 30 минут Минимальные баллы: 36 |
18.06.2021 | ||
|
04.06.2021
|
Русский язык | Продолжительность: 3 часа 30 минут |
18.06.2021 | ||
|
07.06.2021
|
Математика (профильный уровень) | Продолжительность: 3 часа 55 минут Минимальные баллы: 27 |
21.06.2021 | ||
|
08.06.2021
Резерв |
Русский язык | Продолжительность: 3 часа 55 минут (новая категория участников (для аттестата) — 2 часа 30 минут) |
21. |
||
|
11.06.2021
|
Физика | Продолжительность: 3 часа 55 минут Минимальные баллы: 36 |
24.06.2021 | ||
| История | Продолжительность: 3 часа 55 минут Минимальные баллы: 32 |
||||
|
15.06.2021
|
Обществознание | Продолжительность: 3 часа 55 минут Минимальные баллы: 42 |
28.06.2021 | ||
|
16.06.2021
Резерв |
Математика | Продолжительность: 3 часа 55 минут (новая категория участников (для аттестата) — 2 часа) |
23. 06.2021 06.2021 |
||
|
18.06.2021
|
Биология | Продолжительность: 3 часа 55 минут Минимальные баллы: 36 |
01.07.2021 | ||
| Иностранные языки (за исключением раздела «Говорение») | Продолжительность: 3 часа Минимальные баллы: 22 |
||||
|
21.06.2021
|
Иностранные языки (раздел «Говорение») | Продолжительность: 15 минут (по китайскому языку — 12 минут) Минимальные баллы: 22 |
05.07.2021 | ||
|
22.06.2021
|
Иностранные языки (раздел «Говорение») | Продолжительность: 15 минут (по китайскому языку — 12 минут) Минимальные баллы: 22 |
05. 07.2021 07.2021 |
||
|
24.06.2021
|
Информатика и ИКТ | Продолжительность: 3 часа 55 минут Минимальные баллы: 40 |
06.07.2021 | ||
|
25.06.2021
|
Информатика и ИКТ | Продолжительность: 3 часа 55 минут Минимальные баллы: 40 |
06.07.2021 | ||
|
28.06.2021
Резерв |
Литература | Продолжительность: 3 часа 55 минут Минимальные баллы: 32 |
12.07.2021 | ||
| История | Продолжительность: 3 часа 55 минут Минимальные баллы: 32 |
||||
| Русский язык | Продолжительность: 3 часа 30 минут Минимальные баллы: 36 |
||||
| Биология | Продолжительность: 3 часа 55 минут Минимальные баллы: 36 |
||||
| География | Продолжительность: 3 часа Минимальные баллы: 37 |
||||
| Иностранные языки (раздел «Говорение») | Продолжительность: 15 минут (по китайскому языку — 12 минут) Минимальные баллы: 22 |
||||
29. 06.2021 06.2021
Резерв |
Математика (профильный уровень) | Продолжительность: 3 часа 55 минут Минимальные баллы: 27 |
12.07.2021 | ||
| Физика | Продолжительность: 3 часа 55 минут Минимальные баллы: 36 |
||||
| Информатика и ИКТ | Продолжительность: 3 часа 55 минут Минимальные баллы: 40 |
||||
| Обществознание | Продолжительность: 3 часа 55 минут Минимальные баллы: 42 |
||||
| Химия | Продолжительность: 3 часа 30 минут Минимальные баллы: 36 |
||||
| Иностранные языки (за исключением раздела «Говорение») | Продолжительность: 3 часа Минимальные баллы: 22 |
||||
|
02. Резерв |
Математика (профильный уровень) | Продолжительность: 3 часа 55 минут Минимальные баллы: 27 |
12.07.2021 | ||
| Физика | Продолжительность: 3 часа 55 минут Минимальные баллы: 36 |
||||
| Литература | Продолжительность: 3 часа 55 минут Минимальные баллы: 32 |
||||
| Информатика и ИКТ | Продолжительность: 3 часа 55 минут Минимальные баллы: 40 |
||||
| Обществознание | Продолжительность: 3 часа 55 минут Минимальные баллы: 42 |
||||
| История | Продолжительность: 3 часа 55 минут Минимальные баллы: 32 |
||||
| Русский язык | Продолжительность: 3 часа 30 минут Минимальные баллы: 36 |
||||
| Химия | Продолжительность: 3 часа 30 минут Минимальные баллы: 36 |
||||
| Биология | Продолжительность: 3 часа 55 минут Минимальные баллы: 36 |
||||
| География | Продолжительность: 3 часа Минимальные баллы: 37 |
||||
| Иностранные языки (за исключением раздела «Говорение») | Продолжительность: 3 часа Минимальные баллы: 22 |
||||
| Иностранные языки (раздел «Говорение») | Продолжительность: 15 минут (по китайскому языку — 12 минут) Минимальные баллы: 22 |
||||
12. 07.2021 07.2021
|
Литература | Продолжительность: 3 часа 55 минут Минимальные баллы: 32 |
26.07.2021 | ||
| История | Продолжительность: 3 часа 55 минут Минимальные баллы: 32 |
||||
| Биология | Продолжительность: 3 часа 55 минут Минимальные баллы: 36 |
||||
| География | Продолжительность: 3 часа Минимальные баллы: 37 |
||||
| Иностранные языки (раздел «Говорение») | Продолжительность: 15 минут (по китайскому языку — 12 минут) Минимальные баллы: 22 |
||||
13. 07.2021 07.2021
|
Русский язык | Продолжительность: 3 часа 30 минут Минимальные баллы: 36 |
Русский язык | Продолжительность: 3 часа 55 минут (новая категория участников (для аттестата) — 2 часа 30 минут) |
26.07.2021 |
|
14.07.2021
|
Математика (профильный уровень) | Продолжительность: 3 часа 55 минут Минимальные баллы: 27 |
26.07.2021 | ||
| Физика | Продолжительность: 3 часа 55 минут Минимальные баллы: 36 |
||||
| Информатика и ИКТ | Продолжительность: 3 часа 55 минут Минимальные баллы: 40 |
||||
| Обществознание | Продолжительность: 3 часа 55 минут Минимальные баллы: 42 |
||||
| Химия | Продолжительность: 3 часа 30 минут Минимальные баллы: 36 |
||||
| Иностранные языки (за исключением раздела «Говорение») | Продолжительность: 3 часа Минимальные баллы: 22 |
||||
17. 07.2021 07.2021
Резерв |
Математика (профильный уровень) | Продолжительность: 3 часа 55 минут Минимальные баллы: 27 |
26.07.2021 | ||
| Физика | Продолжительность: 3 часа 55 минут Минимальные баллы: 36 |
||||
| Литература | Продолжительность: 3 часа 55 минут Минимальные баллы: 32 |
||||
| Информатика и ИКТ | Продолжительность: 3 часа 55 минут Минимальные баллы: 40 |
||||
| Обществознание | Продолжительность: 3 часа 55 минут Минимальные баллы: 42 |
||||
| История | Продолжительность: 3 часа 55 минут Минимальные баллы: 32 |
||||
| Русский язык | Продолжительность: 3 часа 30 минут Минимальные баллы: 36 |
||||
| Химия | Продолжительность: 3 часа 30 минут Минимальные баллы: 36 |
||||
| Биология | Продолжительность: 3 часа 55 минут Минимальные баллы: 36 |
||||
| География | Продолжительность: 3 часа Минимальные баллы: 37 |
||||
| Иностранные языки (за исключением раздела «Говорение») | Продолжительность: 3 часа Минимальные баллы: 22 |
||||
| Иностранные языки (раздел «Говорение») | Продолжительность: 15 минут (по китайскому языку — 12 минут) Минимальные баллы: 22 |
||||
17. 07.2021 07.2021
|
Математика | Продолжительность: 3 часа 55 минут (новая категория участников (для аттестата) — 2 часа) |
26.07.2021 | ||
|
03.09.2021
|
Русский язык | Продолжительность: 3 часа 55 минут (новая категория участников (для аттестата) — 2 часа 30 минут) |
|||
|
06.09.2021
|
Математика | Продолжительность: 3 часа 55 минут (новая категория участников (для аттестата) — 2 часа) |
|||
13. 09.2021 09.2021
Резерв |
Русский язык | Продолжительность: 3 часа 55 минут (новая категория участников (для аттестата) — 2 часа 30 минут) |
|||
|
15.09.2021
Резерв |
Математика | Продолжительность: 3 часа 55 минут (новая категория участников (для аттестата) — 2 часа) |
|||
| Код | Наименование направления подготовки | Перечень вступительных испытаний с указанием предмета по выбору поступающего (при наличии) | Форма проведения вступительного испытания | |
|---|---|---|---|---|
| Лица, имеющие среднее общее образование |
Лица, имеющие среднее профессиональное образование/ Лица, имеющие высшее образование |
|||
01. 03.02 03.02 |
Прикладная математика и информатика | Информатика | ЕГЭ | Письменный экзамен/ЕГЭ |
| Математика | ||||
| Русский язык | ||||
| 05.03.06 | Экология и природопользование | Биология | ЕГЭ | Письменный экзамен/ЕГЭ |
|
География/Математика (проф. уровень)/Химия/Информатика |
||||
| Русский язык | ||||
| 09.03.01 | Информатика и вычислительная техника | Информатика/Физика | ЕГЭ | Письменный экзамен/ЕГЭ |
| Математика | ||||
| Русский язык | ||||
09. 03.02 03.02 |
Информационные системы и технологии | Физика/Информатика | ЕГЭ | Письменный экзамен/ЕГЭ |
| Математика | ||||
| Русский язык | ||||
| 13.03.01 | Теплоэнергетика и теплотехника | Физика/Информатика | ЕГЭ | Письменный экзамен/ЕГЭ |
| Математика | ||||
| Русский язык | ||||
| 15.03.02 | Технологические машины и оборудование | Информатика/Физика | ЕГЭ | Письменный экзамен/ЕГЭ |
| Математика | ||||
| Русский язык | ||||
15. 03.04 03.04 |
Автоматизация технологических процессов и производств | Информатика/Физика | ЕГЭ | Письменный экзамен/ЕГЭ |
| Математика | ||||
| Русский язык | ||||
| 15.03.06 | Мехатроника и робототехника | Информатика/Физика | ЕГЭ | Письменный экзамен/ЕГЭ |
| Математика | ||||
| Русский язык | ||||
| 18.03.01 | Химическая технология | Химия | ЕГЭ | Письменный экзамен/ЕГЭ |
| Математика | ||||
| Русский язык | ||||
20. 03.01 03.01 |
Техносферная безопасность | Химия | ЕГЭ | Письменный экзамен/ЕГЭ |
| Математика | ||||
| Русский язык | ||||
| 27.03.01 | Стандартизация и метрология | Математика | ЕГЭ | Письменный экзамен/ЕГЭ |
| Физика/Информатика | ||||
| Русский язык | ||||
| 27.03.04 | Управление в технических системах | Математика | ЕГЭ | Письменный экзамен/ЕГЭ |
| Информатика/Физика | ||||
| Русский язык | ||||
29. 03.01 03.01 |
Технология изделий легкой промышленности | Математика | ЕГЭ | Письменный экзамен/ЕГЭ (общеобразовательный предмет) |
|
Физика/Информатика/ Композиция (только для лиц, имеющих среднее профессиональное образование) |
||||
| Русский язык | ||||
| 29.03.02 | Технологии и проектирование текстильных изделий | Математика | ЕГЭ | Письменный экзамен/ЕГЭ |
| Русский язык | ||||
| Композиция | Письменный экзамен | Письменный экзамен | ||
| 29.03.03 | Технология полиграфического и упаковочного производства | Химия | ЕГЭ | Письменный экзамен/ЕГЭ |
| Математика | ||||
| Русский язык | ||||
| 29.03.04 | Технология художественной обработки материалов | Математика | ЕГЭ | Письменный экзамен/ЕГЭ |
| Русский язык | ||||
| Композиция | Письменный экзамен | Письменный экзамен | ||
| 29.03.05 | Конструирование изделий легкой промышленности | Математика | ЕГЭ | Письменный экзамен/ЕГЭ |
| Русский язык | ||||
| Композиция | Письменный экзамен | Письменный экзамен | ||
| 37.03.01 | Психология | Русский язык | ЕГЭ | Письменный экзамен/ЕГЭ |
| Биология | ||||
|
Обществознание/ Математика |
||||
| 38.03.01 | Экономика | Математика | ЕГЭ | Письменный экзамен/ЕГЭ |
|
Обществознание/ Иностранный язык |
||||
| Русский язык | ||||
| 38.03.02 | Менеджмент | Математика | ЕГЭ | Письменный экзамен/ЕГЭ |
|
Обществознание/ Иностранный язык |
||||
| Русский язык | ||||
| 38.03.03 | Управление персоналом | Математика | ЕГЭ | Письменный экзамен/ЕГЭ |
|
Обществознание/ Иностранный язык |
||||
| Русский язык | ||||
| 38.03.04 | Государственное и муниципальное управление | Математика | ЕГЭ | Письменный экзамен/ЕГЭ |
|
Обществознание/ Иностранный язык |
||||
| Русский язык | ||||
| 38.03.06 | Торговое дело | Математика | ЕГЭ | Письменный экзамен/ЕГЭ |
|
Обществознание/История/ Иностранный язык |
||||
| Русский язык | ||||
| 38.03.07 | Товароведение | Математика | ЕГЭ | Письменный экзамен/ЕГЭ |
| Обществознание/История/ Иностранный язык | ||||
| Русский язык | ||||
| 39.03.01 | Социология | Математика/История | ЕГЭ | Письменный экзамен/ЕГЭ |
| Обществознание | ||||
| Русский язык | ||||
| 40.03.01 | Юриспруденция | Обществознание | ЕГЭ | Письменный экзамен/ЕГЭ |
| История/Иностранный язык | ||||
| Русский язык | ||||
| 42.03.01 | Реклама и связи с общественностью | Русский язык | ЕГЭ | Письменный экзамен/ЕГЭ |
| Обществознание | ||||
| История/Иностранный язык | ||||
| 42.03.02 |
Журналистика Профиль: Периодические издания и мультимедийная журналистика |
Русский язык | ЕГЭ | Письменный экзамен/ЕГЭ |
| Литература | ||||
| Обществознание/История | ||||
| 42.03.02 |
Журналистика Профиль: Ведение телевизионных программ |
Русский язык | ЕГЭ | Письменный экзамен/ЕГЭ |
| Обществознание | ||||
| Профессиональное испытание | Устный | Собеседование | ||
| 42.03.04 | Телевидение | Русский язык | ЕГЭ | Письменный экзамен/ЕГЭ |
| Литература | ||||
| Обществознание/История | ||||
| 43.03.01 | Сервис | Математика | ЕГЭ | Письменный экзамен/ЕГЭ |
| Обществознание/История | ||||
| Русский язык | ||||
| 44.03.01 |
Педагогическое образование Профиль: Иностранный язык (английский) |
Иностранный язык (английский язык) |
ЕГЭ | Письменный экзамен/ЕГЭ |
| Обществознание | ||||
| Русский язык | ||||
| 45.03.01 |
Филология Профиль: Отечественная филология (русский язык и литература) Профиль: Зарубежная (славянская) филология |
Литература | ЕГЭ | Письменный экзамен/ЕГЭ |
| Русский язык | ||||
| Обществознание | ||||
| 45.03.01 |
Филология Профиль: Зарубежная филология (гебраистика) |
Литература | ЕГЭ | Письменный экзамен/ЕГЭ |
| Русский язык | ||||
| Иностранный язык | ||||
| 45.03.01 |
Филология Профиль: Русский язык и межкультурная коммуникация |
Обществознание | ЕГЭ | Письменный экзамен/ЕГЭ |
| Русский язык | ||||
| Профессиональное испытание | Устный экзамен | Собеседование | ||
| 45.03.02 | Лингвистика |
Иностранный язык (английский язык) |
ЕГЭ | Письменный экзамен/ЕГЭ |
| Русский язык | ||||
| История/Обществознание | ||||
| 46.03.01 | История | История | ЕГЭ | Письменный экзамен/ЕГЭ |
| Обществознание/Литература | ||||
| Русский язык | ||||
| 50.03.04 | Теория и история искусств | Литература | ЕГЭ | Письменный экзамен/ЕГЭ |
| История/Обществознание | ||||
| Русский язык | ||||
| 51.03.01 | Культурология | Обществознание | ЕГЭ | Письменный экзамен/ЕГЭ |
| История/Иностранный язык | ||||
| Русский язык | ||||
| 51.03.02 |
Народная художественная культура Профиль: Руководство этнокультурным центром |
Русский язык | ЕГЭ | Письменный экзамен/ЕГЭ |
| Литература | ||||
| Мировая художественная культура | Письменный экзамен | Письменный экзамен | ||
| 51.03.02 |
Народная художественная культура Профиль: Руководство любительским хореографическим коллективом |
Русский язык | ЕГЭ | Письменный экзамен/ЕГЭ |
| Литература | ||||
| Исполнительский показ | Классический танец | Исполнение программы | ||
| Народно-сценический танец | ||||
| Постановочный показ | Исполнение хореографического произведения | |||
| Постановка хореографического этюда | ||||
| 52.03.01 | Хореографическое искусство | Исполнительский показ | Классический танец | Исполнение программы |
| Народно-сценический танец | ||||
| Постановочный показ | Исполнение хореографического произведения | |||
| Постановка хореографического этюда | ||||
| Русский язык | ЕГЭ | Письменный экзамен/ЕГЭ | ||
| Литература | ||||
| 53.03.01 | Музыкальное искусство эстрады | Творческое испытание | Исполнение программы | Исполнение программы |
| Профессиональное испытание | Письменно-устный экзамен | Письменно-устный экзамен | ||
| Русский язык | ЕГЭ | Письменный экзамен/ЕГЭ | ||
| Литература | ||||
| 53.03.02 | Музыкально-инструментальное искусство | Творческое испытание | Исполнение программы | Исполнение программы |
| Профессиональное испытание | Письменно-устный экзамен | Письменно-устный экзамен | ||
| Русский язык | ЕГЭ | Письменный экзамен/ЕГЭ | ||
| Литература | ||||
| 53.03.03 | Вокальное искусство | Творческое испытание | Сольное пение | Исполнение программы |
| Профессиональное испытание | Письменно-устный экзамен | Письменно-устный экзамен | ||
| Русский язык | ЕГЭ | Письменный экзамен/ЕГЭ | ||
| Литература | ||||
| 53.03.05 | Дирижирование | Творческое испытание | Дирижиро-вание | Исполнение программы |
| Профессиональное испытание | Сольфеджио, гармония | Письменно-устный экзамен | ||
| Русский язык | ЕГЭ | Письменный экзамен/ЕГЭ | ||
| Литература | ||||
| 50.03.02 | Изящные искусства | Русский язык | ЕГЭ | Письменный экзамен/ЕГЭ |
| Литература | ||||
| Композиция | Письменный экзамен | |||
| 54.03.01 | Дизайн | Русский язык | ЕГЭ | Письменный экзамен/ЕГЭ |
| Литература | ||||
| Рисунок | Письменный экзамен | Письменный экзамен | ||
| Композиция | Письменный экзамен | |||
| 54.03.02 | Декоративно-прикладное искусство и народные промыслы | Русский язык | ЕГЭ | Письменный экзамен/ЕГЭ |
| Литература | ||||
| Композиция | Письменный экзамен | Письменный экзамен | ||
| 54.03.03 | Искусство костюма и текстиля | Русский язык | ЕГЭ | Письменный экзамен/ЕГЭ |
| Литература | ||||
| Рисунок | Письменный экзамен | Письменный экзамен | ||
| Композиция | Письменный экзамен | |||
| 54.03.04 | Реставрация | Русский язык | ЕГЭ | Письменный экзамен/ЕГЭ |
| Литература | ||||
| Композиция | Письменный экзамен | |||
|
Институт медицины и психологии НГУ В. Зельмана |
|||
|---|---|---|---|
|
Лечебное дело 31.05.01 (специалитет) |
Химия | 60 | |
| Биология/Математика | 60/60 | ||
| Русский язык | 60 | ||
|
Лечебное дело 31.05.01 (специалитет, англоязычная программа для иностранных граждан |
Химия | 50 | |
| Биология | 50 | ||
| Английский язык | 50 | ||
|
Психология 37.03.01 |
Биология | 51 | |
| Обществознание | 51 | ||
| Русский язык | 50 | ||
|
Психология 37.03.01 (на базе ВО) |
Биология | 50 | |
| Психология (междисциплинарный экзамен) | 50 | ||
| Русский язык | 50 | ||
|
Гуманитарный институт НГУ |
|||
|
Филология 45.03.01 |
Литература | 61 | |
| Русский язык | 60 | ||
| История/Иностранный язык | 55/55 | ||
|
Фундаментальная и прикладная лингвистика 45.03.03 |
Математика | 62 | |
| Иностранный язык | 55 | ||
| Русский язык | 60 | ||
|
История 46.03.01 |
История | 60 | |
| Обществознание/Иностранный язык | 60/60 | ||
| Русский язык | 50 | ||
|
Востоковедение и африканистика 58.03.01 |
История | 60 | |
| Иностранный язык | 60 | ||
| Русский язык | 50 | ||
|
Лингвистика 45.03.02 |
Иностранный язык | 62 | |
| Русский язык | 60 | ||
| История/Обществознание | 55/55 | ||
|
Журналистика 42.03.02 |
Творческий конкурс | 55 | |
| Литература | 55 | ||
| Русский язык | 55 | ||
|
Институт философии и права НГУ |
|||
|
Юриспруденция 40.03.01 |
Обществознание | 55 | |
|
История/Информатика и ИКТ/ Иностранный язык |
55/55/55 | ||
| Русский язык | 55 | ||
|
Философия 47.03.01 |
Обществознание | 51 | |
|
История/Информатика и ИКТ/ Иностранный язык |
50/55/55 | ||
| Русский язык | 50 | ||
|
Философия (на базе СПО) |
Обществознание | 50 | |
| Философия | 50 | ||
| Русский язык | 50 | ||
|
Механико-математический факультет |
|||
|
Математика и механика 01.03.00 |
Математика | 54 | |
| Информатика и ИКТ/Физика/Химия | 54/54/54 | ||
| Русский язык | 50 | ||
|
Математика и компьютерные науки 02.03.01 |
Математика | 54 | |
| Информатика и ИКТ/Физика/Химия | 54/54/54 | ||
| Русский язык | 50 | ||
|
Факультет естественных наук |
|||
|
Химия 04.03.01 |
Химия | 56 | |
| Физика/Математика | 56/56 | ||
| Русский язык | 56 | ||
|
Фундаментальная и прикладная химия 04.05.01 |
Химия | 56 | |
| Математика/Физика | 56/56 | ||
| Русский язык | 56 | ||
|
Биология 06.03.01 |
Биология | 56 | |
| Математика/Физика | 55/55 | ||
| Русский язык | 55 | ||
|
Физический факультет |
|||
|
Физика 03.03.02 |
Физика | 51 | |
| Математика | 50 | ||
| Русский язык | 50 | ||
|
Физическая информатика 03.03.02 |
Физика | 51 | |
| Математика/Информатика и ИКТ | 50/50 | ||
| Русский язык | 50 | ||
|
Геолого-геофизический факультет |
|||
|
Геология 05.03.01 |
Математика | 50 | |
| Физика/География/Химия | 50/50/50 | ||
| Русский язык | 50 | ||
|
Факультет информационных технологий |
|||
|
Информатика и ВТ 09.03.01. |
Математика | 70 | |
| Информатика и ИКТ/Физика | 70/70 | ||
| Русский язык | 60 | ||
|
Информатика и ВТ 09.03.01. |
Математика | 70 | |
| Информатика и ИКТ/Физика | 70/70 | ||
| Русский язык | 60 | ||
|
Экономический факультет |
|||
|
Экономика 38.03.01 |
Математика | 56 | |
|
Обществознание/История/Информатика и ИКТ/ Иностранный язык |
53/53/53/53 | ||
| Русский язык | 53 | ||
|
Менеджмент 38.03.02 |
Математика | 56 | |
|
Обществознание/История/Информатика и ИКТ/ Иностранный язык |
53/53/53/53 | ||
| Русский язык | 53 | ||
|
Бизнес-информатика 38.03.05 |
Математика | 56 | |
|
Обществознание/История/Информатика и ИКТ/ Иностранный язык |
53/53/53/53 | ||
| Русский язык | 53 | ||
|
Социология 39.03.01 |
Обществознание | 56 | |
|
Математика/История/Информатика и ИКТ/ Иностранный язык |
56/56/56/56 | ||
| Русский язык | 56 | ||
|
Юриспруденция 40.03.01 |
Обществознание | 55 | |
| История/Информатика и ИКТ/Иностранный язык | 55/55/55 | ||
| Русский язык | 53 | ||
|
Высший колледж информатики |
|||
|
Мехатроника и робототехника 15.03.06 |
Физика/Химия/ Информатика и ИКТ | 60/60/60 | |
| Математика | 55 | ||
| Русский язык | 50 | ||
|
Мехатроника и робототехника 15.03.06 (на базе СПО) |
Программные решения | 60 | |
| Цифровые платформы | 55 | ||
| Математика | 55 | ||
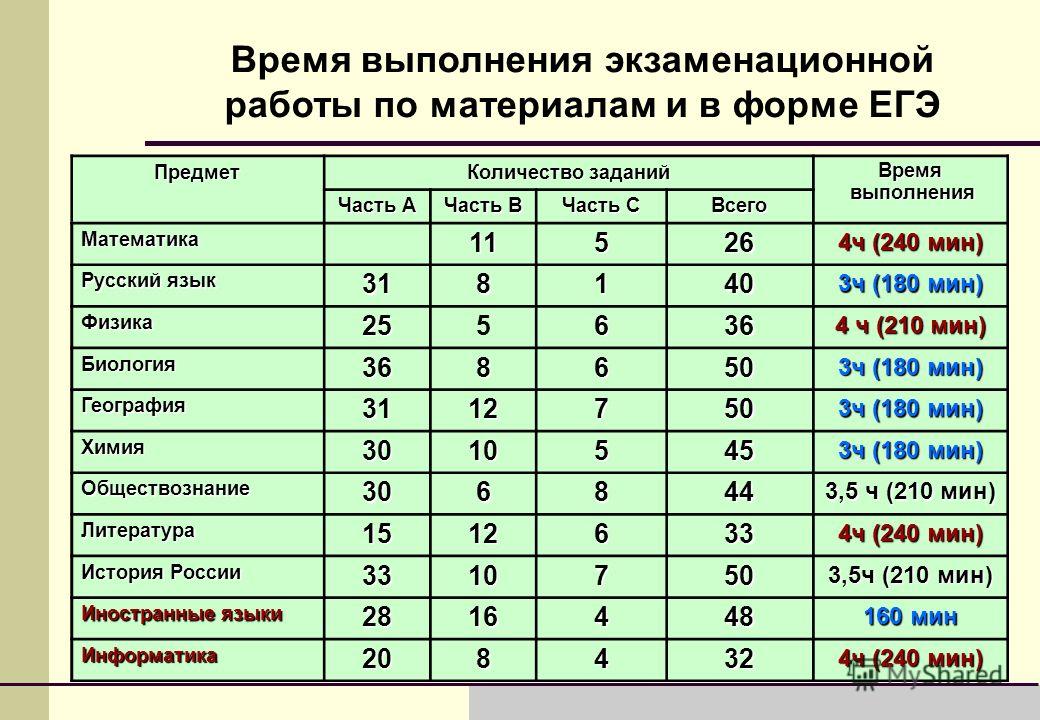
Постигая ЕГЭ: почему обществознание сложнее профильной математики
Стереотип, что ЕГЭ — это угадайка и глупый тест, всё ещё живёт в сознании многих родителей и даже учителей. Однако иногда на экзамене приходится показывать знания на уровне кандидата наук. Наш постоянный блогер, «Учитель года России — 2018» Алихан Динаев, рассказал, какие проблемы он видит в ЕГЭ по обществознанию и почему это один из самых сложных экзаменов.
Полезная рассылка «Мела» два раза в неделю: во вторник и пятницу
В это сложно поверить, но ЕГЭ по обществознанию сейчас сложнее экзамена по профильной математике. Почти неограниченный круг вопросов, тексты из кандидатских диссертаций, неоднозначность подходов и оценки — всё это и многое другое превращает самый популярный предмет по выбору на ЕГЭ в непреодолимое препятствие для тысяч выпускников по всей стране. Вы не согласны? Однако есть множество доводов, подтверждающих это!
Только факты
Самый высокий проходной балл по обществознанию — 42 балла. Больше всего выпускников, не преодолевших минимальный порог, тоже по обществознанию. В некоторых регионах не сдал каждый третий и даже каждый второй. Если по другим предметам средние результаты по стране увеличиваются (по профильной математике, например, за год прирост составил 6 баллов, по информатике — 4, а по истории — 2,5 балла), то по обществознанию результаты даже немного снизились. Среди всех предметов только по биологии и физике средний балл немного ниже, чем по обществознанию. Доля высокобалльников по обществознанию — всего 7,8%. Меньше (7,1%) только по профильной математике. Для сравнения: по русскому тех, кто набрал 80 баллов и выше, — 23,5%.
В чём же причины?
Сам предмет чрезвычайно и даже чрезмерно обширен: экономика и право, политология и социология, философия и культурология, даже немного социальной психологии. При этом круг вопросов, требующих изучения в каждой из этих наук, фактически расширяется с каждым годом, хотя формально кодификатор (список тем на ЕГЭ) не меняется уже много лет.
Содержание КИМов, по моему абсолютному убеждению, крайне и искусственно усложнено. Особенное недовольство учеников вызывают формулировки некоторых заданий, которые даже учителя нередко с трудом понимают.
Взгляните на абзац из текста (задания № 21–24), который попался несчастным выпускникам на досрочном ЕГЭ в этом году:
«Процесс выборов представляет собой средство разрешения спора между субъектами политики, претендующими на доступ к властным ресурсам, в котором коллективным арбитром выступает избирательный корпус (совокупность граждан, обладающих активным избирательным правом). Выборы представляют собой разновидность институционализированного политического конфликта, целенаправленно противопоставляющего политических субъектов, их программы и взгляды».
Вы дочитали? Или бросили на середине? Когда мы начали разбирать этот текст с учениками, то работа превратилась в сплошные мучения и стенания:
— А почему текст такой сложный?
— Здесь столько научных слов!
— Я читаю и ничего не понимаю.
— Вроде каждое слово в отдельности понятно, а вместе вообще неясно.
Это абсурдно сложный наукообразный текст, который не только не интересен ученикам, но и вызывает искреннее возмущение и даже отторжение к предмету.
Почувствовав неладное, я решил поискать источник, и подозрения подтвердились. Оказалось, что это отрывок из диссертации на соискание звания кандидата политических наук. Причём соискатель, защитивший эту диссертацию в МГУ, является специалистом по избирательным вопросам и публикуется почти исключительно в специальных научных журналах, посвященных именно электоральным проблемам.
Теперь задумайтесь: на итоговом экзамене, от результата которого во многом зависит судьба юноши или девушки, дают текст кандидатской диссертации, доверху напичканный научными терминами и непонятный большинству взрослых.
Обществознание — бесполезный предмет?
Из уст учителя обществознания, наверное, это звучит дико. Я так, конечно, не считаю, но таково мнение россиян, опрошенных недавно ВЦИОМ. Социологи спрашивали, какой из школьных предметов пригодится детям в будущем. На вершине рейтинга оказались математика и русский язык. В числе явных аутсайдеров — ИЗО, музыка и (вы уже, наверное, догадываетесь) обществознание — 6%! То есть лишь один из 16–17 опрошенных счёл, что это полезный для жизни предмет. Экономику полезной назвали и вовсе 2%, а правоведение — вообще 1%! Эти цифры удивили и возмутили. Это притом что в России крайне низкий уровень правовой и финансовой грамотности.
Я-то как раз всю жизнь был уверен, что именно обществознание — самый практико-ориентированный и применимый в реальной жизни школьный предмет. Да, всяк кулик своё болото хвалит, но дело в том, что обществознание учит детей, какие у них есть права и как их защищать, учит правильно обращаться с деньгами, кредитами, инвестициями, объясняет, как строить бизнес и как его вести, даёт знания о важнейших законах страны, позволяет понять, как работают банки, биржи, деньги и так далее. Список можно продолжать долго. Почему же тогда взрослые и дети называют обществознание (экономику, право, социологию, политологию, психологию) бесполезным предметом?
Уверен, что одна из причин — это то самое пугающее и вызывающее неприязнь наукообразие. Настоящее засилье наукообразия, едва ли не культ гиперболизированного научного стиля, который абсолютно не соответствует ни возрастным, ни психологическим особенностям старшеклассников.
Непредсказуемость
Есть и ещё одна проблема, делающая ЕГЭ по обществознанию очень тяжёлым. Выпускники должны быть готовы к тому, что им могут встретиться задания, которые они никогда не видели. Вообще. Нигде. Ни в одном сборнике. Даже в сборниках от разработчиков ЕГЭ. Такое, наверное, случается только на экзамене по обществознанию. Например, задания № 27 в этом году стали похожи на монстров, состоящих из 4–5 нагромождённых друг на друга вопросов. Ни в одном сборнике подобных заданий не было.
Самая нелюбимая «песня» выпускников — это задание № 25, где нужно давать определения. Знать их, конечно, хорошо, но разумно ли спрашивать определения сложных, неоднозначных и далёких от реалий школьной и студенческой жизни терминов, таких как «политический процесс» или «метод научного познания?» Сколько копий было сломано, например, с формулировкой термина «политический процесс», который разные политологи понимают совершенно по-разному, даже говорить не хочется.
Отдельная история — это задания № 24. Это почти лотерея: одним повезёт, и там попадётся что-то знакомое и решаемое, другим не повезёт, и там окажется вопрос, содержание которого требует знаний, выходящих за пределы школьного курса. Например, в этом году почти все выпускники завалили задание № 24, где их просили назвать три способа снижения риска инвестиций в ценные бумаги. Мне как человеку, увлекавшемуся этой темой, в голову сразу пришёл такой ответ: технический анализ, фундаментальный анализ, диверсификация активов, хеджирование рисков, покупка ценных бумаг с гарантированной доходностью. Сколько 17-летних юношей и девушек в стране могут ответить так? Интересно, сколько человек из 100 опрошенных на улице ответили бы на этот вопрос. Один? Возможно, хотя и оптимистично.
Субъективность
Обществознание, если можно так выразиться, слишком гуманитарный предмет. Здесь слишком много разных мнений, подходов и концепций. Это явно прослеживается при оценке работ экспертами. Во время апелляций нередки случаи, когда три эксперта, сидящие в метре друг от друга, дают три совершенно разных ответа на один и тот же вопрос, смотря на одну и ту же ситуацию с совершенно противоположных сторон.
У меня нет статистики, но рискну предположить, что больше всего апелляций подают именно по обществознанию.
Ту же субъективность можно увидеть и в критериях. Камнем преткновения для тысяч выпускников в нашем регионе в этом году стал план (задание № 28) на тему «Человек на рынке труда». Некоторые написали план из десяти пунктов, рассказали о видах рынков и безработицы, способах борьбы с ней, участниках рынка труда, указали, что на этом рынке есть спрос и предложение, а в итоге получили ноль. Почему? Потому что в критериях были эти пункты, но составители сочли их «необязательными», а вот неочевидные моменты (от чего зависит зарплата, например) стали «обязательными».
После этого я взял план на эту тему из специального сборника с планами, а также нашёл вариант ответа на «Решу.ЕГЭ» и убедился, что ни тот, ни другой максимального балла не получил бы…
Для одной статьи проблем слишком много.
Вы находитесь в разделе «Блоги». Мнение автора может не совпадать с позицией редакции.
Какое математическое образование может подготовить студентов к жизни в обществе будущего?
Несмотря на то, что навыки 21 века доминируют в (публичных) дискуссиях об образовании будущего, мы считаем, что содержание, которое необходимо преподавать, не менее важно, особенно в случае математики. На наш взгляд, математическое образование должно готовить учащихся к применению математики во всех видах рабочих и повседневных ситуаций. Далее мы в первую очередь рассмотрим использование математики с учетом возможностей трудоустройства, поскольку именно здесь мы видим наибольшее влияние цифровизации нашего общества.Чтобы понять, каковы на самом деле требования математики, мы рассмотрим три разных точки зрения. (1) Поскольку математика на рабочем месте значительно отличается от школьной математики, мы попытаемся отобразить характеристики математики на рабочем месте , чтобы получить представление о том, к какой математической деятельности ученики должны быть готовы. (2) Чтобы предвосхитить требования 21 века, мы возьмем за отправную точку перспективу того, что все будут работать в компьютеризированной среде.Здесь мы будем использовать более аналитический подход при попытке определить математические компетенции , которые дополняют работу компьютеров . (3) Наконец, мы будем размышлять о том, как растущее использование информационных технологий повлияет на математические темы, которые приобретают значение под влиянием использования информационных технологий, чтобы определить, какое математическое содержание необходимо будет реализовать.
Характеристики математики на рабочем месте
Многие исследователи математики на рабочем месте обнаружили, что математика, которой люди занимаются вне школы, значительно отличается от характера школьной математики (Lave, 1988; Nunes, Schliemann & Carraher, 1993; Saxe , 1988).Несмотря на то, что после этих исследований требования к рабочему месту изменились, текущие исследования продолжают выявлять разрыв между математикой на рабочем месте и школьной математикой (FitzSimons, 2013; Wedege, 2002). Поэтому мы считаем целесообразным изучить характер рабочего места, чтобы раздвинуть границы того, как должна выглядеть математика для достижения успеха в будущем.
Неформальный характер математики на рабочем месте.
За последние несколько десятилетий большая часть работ была сосредоточена на математике взрослых и рабочих в самых разных культурах.Примеры этого типа анализа включают математику плотников (Millroy, 1991), строителей бассейнов (Zevenbergen, 1997), каменщиков (Moreira & Pardal, 2012), строителей (Bessot, 1996), медсестер (Hoyles, Noss & Pozzi, 2001). ) и инженеров-строителей (Gainsburg, 2007), и это лишь некоторые из них. Главный вывод из этих исследований заключается в том, что математика, которую преподают в школе, обычно не та математика, которую люди используют для достижения успеха на рабочем месте (Marr & Hagston, 2007; Mills, 2012; Wedege, 2002).Например, медсестры не используют общепринятые стратегии пропорционального мышления, которым обучают в школе (например, перекрестное умножение), для определения подходящих соотношений для введения лекарств пациентам. Скорее они используют более эффективные, неформальные стратегии, типичные для их ситуации. Фактически, одно исследование показало, что, хотя большинство медсестер не проходят тесты пропорций в школе, они на 100% точны при назначении лекарств в правильных пропорциях с использованием лично разработанных стратегий (Hoyles, Noss, Kent & Bakker, 2013; Perlstein, Callison , White, Barnes & Edwards, 1979).
Значение контекста на рабочем месте.
Несмотря на призывы многих научных, исследовательских и математических организаций к контекстуализации математики, многие школы продолжают представлять математику как абстрактные, деконтекстуализированные задачи. Напротив, исследования математики на рабочем месте показывают, что математика обычно не выполняется вне контекста, состоящего из целей и задач. Например, на рабочем месте редко можно встретить отдельные случаи выполнения десятичных операций.Скорее, большинство вычислений выполняется в таких областях математики, как алгебра, числа и геометрия, и являются частью контекстуализированной проблемы (Wake & Williams, 2001). На этом фоне преподаватели STEM рекомендуют изучать математику, представляя задачи в реалистичных контекстах, таких как биология, физика, инженерия и т. Д. (Например, Cox, Reynolds, Schunn & Schuchardt, 2016). Здесь необходимы два слова предостережения. English (2016) отмечает, что в исследованиях STEM математика, как правило, отодвигается на второй план, отодвигая ее до , поддержки для контекстов STEM, а не для самостоятельной важности.Во-вторых, контексты, которые используются в обучении математике, имеют тенденцию отражать надуманные ситуации, а не те, которые действительно реалистичны и являются богатыми площадками для математизации. Одно отмеченное исключение – это работа, проделанная исследователями из Института Фройденталя (Freudenthal, 1991; Gravemeijer, 2008).
Работники не только используют ситуативные неформальные математические стратегии, но они также обычно не считают себя «занимающимися математикой» в своей работе, хотя посторонний может найти математику в изобилии своей деятельности (Mills, 2012; Nicol, 2002) .Уэйк и Уильямс (2001) используют теорию деятельности, чтобы объяснить, что математика на рабочем месте и в школе / колледже – это разные жанры, которые пересекаются и имеют определенные границы. С одной стороны, школьная математика находится под влиянием формальной профессиональной практики математиков и учителей, изучающих математику в этой системе. С другой стороны, в математике на рабочем месте преобладают практические задачи с инструментами, практиками и дискурсом, специфичными для разных культур (Wake & Williams, 2001). Это наблюдение ведет непосредственно к следующей характеристике математики на рабочем месте – значению контекста в обоих жанрах.
Инструменты, методы и беседы на рабочем месте.
Математические инструменты, практики и дискурс можно рассматривать как сформированные в зависимости от целей и проблем, возникающих на рабочем месте (Magajna & Monaghan, 2003). Например, Уильямс, Уэйк и Борехэм (2001) представляют анализ математики рабочих в промышленной химической лаборатории, в которой сотрудники эффективно используют неканонические графики, которые значительно отличаются от обычных графиков, изученных в колледже.Хойлс и Носс (Hoyles, Noss, Kent & Bakker, 2010) придумали термин «техно-математическая грамотность» (TmLs). TmL определяются как идиосинкразические формы математики, которые формируются практиками, задачами и инструментами на рабочем месте. TmL состоят из комбинации математических и контекстных знаний.
Уникальное использование рабочих инструментов определяется целью, для которой они их используют. Школьные математические практики рассматривают артефакты как концептуальные инструменты, а не как практические инструменты на рабочем месте (Jurdak & Shahin, 2001).Уэйк и Уильямс (2001) предполагают, что цель использования инструментов в школьных условиях – сдать экзамен. Рабочие, напротив, мотивированы на использование определенных инструментов для достижения четко определенных целей для клиентов. Например, школьники интерпретируют и рассуждают с помощью декартовых графиков очень формально, в то время как работники химической лаборатории строят их для своей собственной эффективности (например, имея наименьшее значение переменной справа от оси x).
В зависимости от рабочего места и школьного жанра различаются не только типы инструментов и действий с ними, но и методы.Практики решения проблем в обоих жанрах также существенно различаются. Мы уже упоминали, что работники используют инструменты иначе, чем студенты, из-за их общей цели – удовлетворить начальника или клиента. Кроме того, сотрудники часто сталкиваются со сложными и запутанными проблемами, которые могут иметь несколько правильных решений. Для них цель – найти эти решения и работать в рамках ограничений ситуации, чтобы выбрать наиболее жизнеспособный путь (Brady, Eames & Lesh, 2015). Например, наиболее эффективное решение проблемы архитектурного проектирования может оказаться не самым дешевым, и фирма может проиграть заявку, если представит его покупателю.Следовательно, при выборе пути решения необходимо учитывать определенные компромиссы. Это отличается от школьной математики, в которой учителя представляют аккуратных задач с одним правильным решением. Цель студентов – найти это решение, чтобы сдать экзамен. Кроме того, проблемы создает учитель, тогда как на рабочем месте проблемы часто создает работник. Чтобы подчеркнуть этот момент, инженеры в исследовании Тосмур-Баязита и Убуза предложили такие изменения в методах обучения, чтобы инструкция не только касалась правильного решения уравнений, но и фокусировалась на том, как представить ключевые особенности реального явления (Тосмур-Баязит & Убуз, 2013).
Дискурс на рабочем месте также радикально отличается от школьной обстановки. Значения определенных математических символов и слов обсуждаются в контексте деятельности, в которой участвуют работники или студенты (Wake & Williams, 2001). Это означает, что математический язык и символы, которые используют рабочие, могут не иметь формального значения, которое они имеют в школьных условиях (вспомните своеобразное использование декартовой плоскости химиками в лаборатории).
Изменения во времени.
Технологический прогресс быстро меняет роль квалифицированных и неквалифицированных рабочих на рабочем месте. Функции планирования в организации когда-то были прерогативой работников управленческого звена; однако технологии взяли на себя работу многих неквалифицированных рабочих, которым для достижения успеха на рабочем месте требуется другой набор навыков (Wedege, 2002). Развитие технологических устройств в корне уменьшило потребность в вычислениях на рабочем месте, и часто работники не осознают необходимость и присутствие математики в своей работе.Технологии также превратили математику в черный ящик, сделав математику невидимой для рабочего (Williams & Wake, 2007a). Глобализация рабочего места теперь позволяет предприятиям производить продукты для клиентов по всему миру по индивидуальному заказу. Таким образом, глобализация привела к тому, что практика на рабочем месте сместилась от создания прототипов продукта (один размер подходит всем) к использованию математических рассуждений и критического мышления для настройки продуктов. Поскольку сложная математика скрыта в технологических черных ящиках, крайне важно, чтобы работник понимал математические вычисления в достаточной степени, чтобы создавать входные данные и интерпретировать выходные данные технологии (Kent, Noss, Guile, Hoyles & Bakker, 2007; Gainsburg, 2007).Сотрудники также должны уметь передавать математику черного ящика своим коллегам и начальникам (Williams & Wake, 2007b). Учитывая необходимость передачи математики, скрытой в технологических черных ящиках, неудивительно, что работодатели рассматривают общение и критическое мышление как одни из самых важных навыков, которые они ищут от выпускников колледжей (Hoyles, Wolf, Kent & Molyneux-Hodgson, 2002).
Этот очерк характеристик математики на рабочем месте предлагает основу для обсуждения целей математического образования.Однако, чтобы определить цели на будущее, мы должны быть более конкретными из-за возросших требований цифрового общества. Теперь мы переходим к обсуждению математических способностей, на которые влияет компьютерный век.
Математические навыки, дополняющие работу компьютеров
Если признается, что одна из целей математического образования состоит в том, чтобы подготовить учащихся к жизни и работе, вышеупомянутые характеристики рабочего места должны быть приняты во внимание в математическом образовании.Эта идея не нова; это отражается в призывах к моделированию и применению, а также к использованию аутентичных проблемных ситуаций в образовании. В настоящее время последний является одним из основных лидеров STEM-движения. Обратной стороне медали, однако, уделяется меньше внимания, а именно: характер преподаваемой математики также должен быть адаптирован. Математика, изучаемая в школе, должна позволять гибкое использование и адаптацию. В связи с этим мы можем вспомнить Фройденталя (1968), который еще в 1960-х говорил о полезности преподавания математики.Он утверждал, что формальная математика обычно применима в теории, но только для экспертов с высоким уровнем знаний, а не для среднего студента. Мы вернемся к этому вопросу позже.
Во-первых, мы хотим подчеркнуть, что когда мы рассматриваем математическое образование в будущем, это больше, чем ожидание характеристик рабочего места. Мы движемся в будущее, в котором машины будут выполнять все математические вычисления. Таким образом, возникает вопрос: «Какой математике мы учим, когда компьютеры делают всю математику?» (Вольфрам, 2010).Вольфрам (2010) пытается ответить на этот вопрос, анализируя, что задействовано в математике в реальном мире. Он утверждает, что это включает следующие шаги:
-
Понимание того, где применима математика
-
Перевод практических задач в математические задачи
-
Решение математической задачи
-
Интерпретация и оценка результатов
Он отмечает, что обычно в математическом образовании систематически рассматривается только третий шаг, и что это именно тот шаг, который все чаще выполняется компьютерами! В математическом образовании внимание должно быть переключено на три других шага.Более того, как стало ясно в исследованиях на рабочем месте, когда компьютеры выполняют математические вычисления, нужно понимать математику, лежащую в основе этих вычислений.
Мы можем объединить первый, второй и последний этап под заголовком «моделирование и применение», отделив «проверку расчетов» от интерпретации и оценки результатов. Как мы убедимся позже, приоритетность проверочных расчетов над выполнением стандартных процедур имеет значительные последствия для содержания и структуры учебной программы.Это предлагает нам три категории для обсуждения того, какие математические компетенции необходимы для цифрового общества: применение / моделирование , понимание и проверка .
Применение / Моделирование.
Моделирование и приложения уже давно находятся в повестке дня Международного сообщества преподавателей математического моделирования и прикладных программ (ICTMA). Однако моделированию в повседневной школьной практике уделяется мало внимания.Исследования моделирования в математическом образовании имеют тенденцию больше сосредотачиваться на роли моделирования в обучении и реализации определенных математических концепций (Gravemeijer, Lehrer, van Oers & Verschaffel, 2002). Однако мотивация для создания и интерпретации моделей на рабочем месте состоит в том, чтобы математизировать реалистичную ситуацию с целью ответа на практический вопрос, а не для изучения математической идеи. Заметным исключением в сфере образования является работа в группе «Моделирование и моделирование перспективы» (Hamilton, Lesh, Lester & Brilleslyper, 2008), которая разработала один из наиболее разработанных учебных подходов, направленных на развитие у учащихся навыков моделирования, обозначенных как Model Eliciting Activities (МПС).Образцовая деятельность по выявлению задумана как подлинная проблема в реальной ситуации, которая требует от учащихся создания модели для интерпретации, объяснения и прогнозирования этой ситуации для решения проблемы. Эти MEA также рассматриваются как катализатор образования в области STEM; в этом отношении Hamilton et al. (2008) особенно указывают на возможности соединения математики и инженерии.
Мы можем расширить это обсуждение различий между решением реальных задач в цифровом обществе и школьной математикой на основе Brady et al.(2015). Они делают следующие наблюдения, в которых повторяется большая часть выводов, представленных в разделе о рабочем месте. Люди часто работают в группах, чтобы воспользоваться разнообразным опытом, которым они могут поделиться. При решении проблем в реальности потребности реального клиента определяют критерии, которым должно соответствовать решение. В то же время, однако, качества, которые клиент считает важными, могут потребовать дальнейшего уточнения или практического применения. Работа с конкретным клиентом часто также определяет, какие измерения доступны, в то время как источники данных, возможно, придется сначала интерпретировать или создавать.Также типично для реальных проблем, что решения должны учитывать неопределенные или меняющиеся условия и компромиссы.
Чтобы определить компетенции, необходимые для моделирования реальных проблем, мы можем взглянуть на математическую структуру PISA 2015 (OECD, 2016). Эта структура содержит те же шаги, которые Вольфрам (2010) использует для описания процесса моделирования реальных проблем и которые можно найти в большинстве моделей решения реальных проблем (Verschaffel, Greer & De Corte, 2000; Vorhölter, Kaiser & Ferri, 2014).Помимо математических знаний, концепций и навыков, структура ссылается на различные математические возможности, которые особенно важны для моделирования. Эти компетенции отражают два основных вида деятельности, которые мы поместили в категорию применения и моделирования: переход от реальности к математике и переход обратно от математики к реальности. В связи с переходом от реальности к математике в структуре упоминаются такие возможности, как декодирование и интерпретация информации, структурирование и концептуализация проблемной ситуации, выполнение умозаключений и предположений, а также формулирование модели.Что касается обратной деятельности, они упоминают способности, такие как обобщение и представление результатов, а также предоставление объяснений или обоснований, а также интерпретация или оценка математического результата. Кроме того, они также относятся к использованию графиков, таблиц, диаграмм, изображений, уравнений и формул. Отметьте, что, как мы отметили выше, моделирование включает использование математических концепций и процедур, которые разработчики моделей должны связывать с приложениями, что часто является проблемой школьной математики. Таким образом, использование моделирования и применения в качестве целей имеет последствия для характера преподаваемой математики.Мы более подробно остановимся на этом вопросе при обсуждении категории «понимание».
Однако есть еще один момент, который мы хотим поднять: не все рабочие будут активными моделистами. Во многих случаях они будут использовать модели, изобретенные другими. В этом отношении мы утверждаем, что понятие техно-математической грамотности обычно указывает на необходимость понимания скрытой, своеобразной математики, которая формируется инструментами и методами, разработанными другими.Кроме того, может быть более распространенным, что работники должны использовать или адаптировать результаты моделирования других людей. Ольденбург (2011), например, отмечает, что на рабочем месте люди довольно часто сталкиваются с проблемой и выбирают из множества уже созданных моделей, хотя может случиться так, что предварительно структурированную модель необходимо изменить и, таким образом, она может развиваться как он используется в различных ситуациях. С точки зрения Ольденбурга (2011), стрелка от реального мира к моделям также должна указывать назад.Таким образом, необходимо учитывать оба типа моделирования. Мы можем также добавить, что помимо участия в моделировании или использовании моделей, многие люди будут использовать результаты работы по моделированию, выполненной другими. Это также повлияет на необходимые навыки моделирования.
Мы можем закрыть этот раздел кратким обсуждением препятствий, которые могут возникнуть при обучении. Часто учителя рассматривают контексты реального мира только как инструменты мотивации и мало обращают внимание на эти контексты.Многие учителя быстро превращают контекстную проблему в математическую, выдвигая на первый план вычисления, которые необходимо выполнить. В связи с этим Томпсон, Филипп, Томпсон и Бойд (1994) говорят о расчетной ориентации, которую они противопоставляют концептуальной ориентации. Учителя, ориентированные на вычисления, склонны игнорировать как контекст, так и то, как вычисления возникают из понимания контекста. Они в основном говорят в терминах чисел и операций, сосредотачиваются на идентификации и выполнении процедур и стремятся получить численные решения.Учителя с концептуальной ориентацией, напротив, стремятся к концептуальной согласованности и сосредотачиваются на поддержке учащихся в осознании роли и значения числовых значений в ситуации и того, как это переводится в числовые операции. Смысл этой работы состоит в том, что концептуальная ориентация на математику больше способствует пониманию математического моделирования.
Понимание.
Рабочие места не только становятся все более автоматизированными, но компании также пытаются гибко реагировать на потребности клиентов.Следствием этого является то, что сотрудники на многих уровнях должны понимать, что происходит, чтобы иметь возможность общаться как с коллегами, так и с клиентами. Тезис о том, что людям необходимо понимать математику, которая используется в рабочих машинах, подтверждается наблюдениями за высокотехнологичными рабочими местами (Kent et al., 2007; Gainsburg, 2007).
Мы увидели, что знания на рабочем месте обычно индивидуальны и привязаны к конкретным контекстам и инструментам. В связи с этим мы уже упоминали понятие TmLs (Hoyles & Noss, 2003).Эти TmL состоят из комбинации математических и контекстных знаний. Возникает вопрос: какая форма математических знаний может лучше всего подготовить студентов к присвоению TmL? Кажется самоочевидным, что понимание основных концепций будет более полезным, чем овладение жесткими процедурами. Обратите внимание, что это не меняет того факта, что также потребуется некоторый уровень процедурного мастерства, хотя бы только для разработки этих концепций. Однако мы можем утверждать, что с увеличением доступности технологий потребность в овладении рутинными навыками уменьшается.Это создает пространство для работы над концептуальным математическим пониманием, которое необходимо для понимания математики, которая скрыта в цифровых инструментах, которыми изобилует наше технологическое общество. Говоря о концептуальном понимании, мы можем сослаться на хорошо известное различие, которое Скемп (1978) проводит между инструментальным и реляционным пониманием. Мы можем пояснить разницу, взяв в качестве примера среднее арифметическое. Инструментальное понимание среднего относится к пониманию процедуры и рецепта: сложите отдельные меры и разделите их на количество мер.Понимание отношений касается концептуального значения. Среднее значение относится к значению, которое достоверно представляет меры в наборе данных. В качестве метафоры мы можем думать о «среднем человеке». В основе концепции лежит концепция индивидуальных расстояний между средним значением и другими значениями данных, которые в сумме равны нулю. Концептуальное понимание среднего также включает понимание чувствительности среднего к асимметричному распределению или экстремальным значениям.
Наряду с взаимопониманием, к которому мы должны стремиться, нам нужно будет рассмотреть, какой уровень понимания необходим и для кого.Мы можем предположить, что во многих случаях будет достаточно какого-то глобального, общего понимания. В связи с этим мы можем сослаться на работы Капута (1994, 1997), который в 1990-х годах привлек внимание к тому факту, что рост компьютеризации создал потребность в обучении математическому анализу гораздо большей части населения. Он утверждал, что только 10% студентов получили доступ к математическому анализу, хотя гораздо большая часть населения должна была знать идеи и методы вычисления.В связи с этим он призвал «демократизировать доступ к математике изменений и вариаций» (Vahey, Lara-Meloy & Knudsen, 2009, p. 417). Чтобы удовлетворить остальные 90% студентов, нам нужно сосредоточиться на «ключевых базовых идеях скорости изменения, накопления, связи между переменными темпами и накоплением, а также приближения» (Капут, 1997, стр. 733). По его мнению, это может быть достигнуто путем развертывания динамических представлений, которые позволяют компьютеры, из которых работает над SimCalc (Roschelle et.al., 2010) является примером. В заключение мы можем утверждать, что тезис Капута (1997) будет актуален для многих других тем в наши дни; В цифровом обществе люди должны понимать ключевые идеи, лежащие в основе математики, используемой машинами. Это находит отклик в работе Hoyles and Noss cum suis (Hoyles, Noss, Kent & Bakker, 2010), которые также выступают за концептуальное понимание задействованной математики и разрабатывают артефакты, такие как компьютерные инструменты, для поддержки рабочих в развитии этого понимания.
Это подводит нас к роли компьютерных инструментов, специально созданных для поддержки разработки и реализации ключевых идей в конкретных областях. Наряду с компьютерными инструментами, разработанными группой Hoyles cum suis (например, Bakker, Kent, Noss & Hoyles, 2009), и программным обеспечением Simcalc, разработанным Kaput и соавторами, мы можем ссылаться на компьютерные инструменты, разработанные в экспериментах по дизайну, некоторые из нас принимали участие, например, в анализе данных (Cobb, McClain, & Gravemeijer, 2003), исчислении (de Beer, Gravemeijer & van Eijck, 2015; Doorman & Gravemeijer, 2009) и функциях (Doorman, Drijvers, Gravemeijer, Boon И Рид, 2012).На наш взгляд, при рассмотрении того, какой предмет может быть приемлемым для большинства студентов, следует принимать во внимание цель схватки с ключевыми идеями и потенциал специализированных образовательных компьютерных инструментов для достижения этой цели.
Проверка.
Важным аспектом оценки результата компьютерного ответа на некоторую проблему является вопрос о том, насколько результаты соответствуют контексту проблемы и возможно ли решение в этом контексте.Другой аспект касается математической корректности вычисленного результата. Мы можем начать с того, что отметим, что идея состоит не в том, что пользователи компьютеризированной аппаратуры должны повторять вычисления вручную. Вместо этого мы хотим, чтобы они могли проверить, кажется ли результат правдоподобным. На наш взгляд, это имеет серьезные последствия для учебной программы по математике. Мы можем проиллюстрировать это, проверив ответ на арифметический расчет. Здесь можно выполнить некоторую «глобальную арифметику», изменив числа, чтобы упростить вычисление, и используя это модифицированное вычисление, чтобы судить, является ли ответ разумным.Разрабатывая этот пример, мы хотим пояснить, что для этого требуется другой вид арифметики, нежели тот, который преподается в настоящее время.
В основе глобальной арифметики лежат гибкие рассуждения с числовыми отношениями, работа с нулями и арифметическими свойствами (Gravemeijer, 2015). Возьмем для примера 78 × 1261. Это может быть приблизительно 75 × 1200, используя 12 = 4 × 3, таким образом, 1200 = 4 × 300, и 75 × 4 = 300 и 300 × 300 равно
, или 80 × 1250, и используя 8 × 125 = 1000 и 1000 × 100 = 100000.Gravemeijer (2015) утверждает, что использование числовых отношений является ключевым здесь; когда решатель задач использует числовые отношения, которые знакомы и готовы к использованию, он или она может быть уверен в правильности приближения. Следуя этой цепочке рассуждений, мы можем сделать вывод, что мы должны поддерживать учащихся в разработке числовых отношений, которые могут использоваться в различных вычислительных ситуациях (например, кратные 25, 75, 125 и т. Д., И связи этих чисел с десятичные дроби, дроби и проценты). В идеале ученики должны разработать сети числовых отношений, которые они могут гибко соединять, что, в свою очередь, может укрепить их уверенность в числовых отношениях, которые им знакомы.Мы можем добавить, что гибкое использование числовых отношений также подразумевает использование арифметических свойств, таких как коммутативность, ассоциативность и распределенность, для подготовки студентов к алгебре.
Мы можем также отметить, что проверка математической корректности включает в себя больше, чем глобальный пересчет. Математическая корректность может также касаться адекватности математических процедур, приближений или обобщений. В связи с этим мы можем указать на Левитина (2016), который исследовал, как посторонние могут судить о достоверности и достоверности результатов статистических процедур, выполненных другими.
Приведенный выше арифметический пример показывает, что учебная программа, направленная на развитие арифметических навыков, необходимых для проверки результатов работы компьютера, будет значительно отличаться от обычной учебной программы, направленной на быстрое получение точных ответов. То же самое и со статистикой, особенно потому, что усилия, направленные на то, чтобы помочь студентам получить опыт ведения статистики, часто связаны с ограниченными экспериментами, которые просто не соответствуют требованиям, к которым «потребители статистики» должны критически относиться (Левитин, 2016).
Профиль Андрея Окунькова
Для своих коллег удостоенный наград математик Андрей Окуньков – «семьянин», прозвище, которое может относиться как к его воспитанию, так и к его исследованиям, объединяющим многие разделы математики. Будучи аспирантом, Окуньков обдумывал свою диссертационную задачу, катая свою первую дочь в коляске холодными русскими зимними ночами.
Его вторая дочь родилась, когда он работал постдоком в Чикагском университете.«У нас был письменный стол с моим компьютером, и у меня была эта маленькая люлька, поэтому я перемещал ее одной рукой и печатал другой», – вспоминает Окуньков, исследователь Саймонса по математике и старший научный сотрудник Саймонса. Общество стипендиатов. «Теперь я думаю об этом, как это возможно?»
Опять же, Окуньков привык к «невозможному». Его специальность – объединение разрозненных людей и идей; он получил медаль Филдса (часто называемую «Нобелевской премией по математике») за «свой вклад, объединяющий вероятности, теорию представлений и алгебраическую геометрию», согласно заявлению о награде.Его творчество отражает вековой идеал математики, который редко реализовывался со времен Возрождения: все математические области являются частью одного большого генеалогического древа и содержат связи, ожидающие своего открытия.
Диссертация Окунькова и несколько его статей 1990-х годов решали проблемы в подполе, называемой теорией представлений. Некоторые из его технических идей с тех пор использовались в самых разных областях, от дифференциальной геометрии до теории чисел. В 2000-х он доказал известные гипотезы теории вероятностей и математической физики; некоторые из его работ с двумя алгебраическими геометрами и физиком-теоретиком стали частью основ перечислительной геометрии.
«Андрей действительно одарен, так это налаживать эти связи, – говорит его соратник Давеш Маулик, который был аспирантом, когда впервые встретил Окунькова в 2002 году. того, что было обычным делом, как и 100 лет назад, но по мере того, как математика становится более специализированной, выполнять ее становится все труднее ».
Строим корни
Окуньков пошел относительно окольным путем к чистой математике, поступив в колледж по специальности экономика.В то время российская экономика включала в себя политическую философию, и молодой Окуньков думал, что может применить экономические идеи для улучшения общества. Но после службы в мирное время, когда его призвали в армию, он передумал и перешел на математику, получив высшее образование в 1993 году.
«Конечно, решать задачи по математике намного проще, чем решать проблемы общества», – говорит Окуньков, уголки его глаз морщатся от его вездесущей улыбки. «Я дорожу тем фактом, что математика в целом аполитична.Одна и та же теорема остается верной, независимо от того, согласен я или нет с человеком, который доказал их на какой-либо политической основе ».
Во время экономического хаоса, последовавшего за распадом СССР в 1991 году, Окуньков нашел работу в Институте проблем передачи информации в России, работая над докторской степенью. Он работал в теории представлений, которая изучает математические объекты, анализируя их симметрии. Например, можно изучить атом водорода, рассматривая движения его единственного электрона и симметрии этих движений.
После защиты диссертации Окуньков отправился в США. По счастливой случайности его академическая карьера совпала с карьерой его жены в области финансов: когда Окуньков начал свою постдокторскую деятельность в Чикагском университете в 1996 году, его жена Инна Окунькова поступила на программу MBA там. ; его должность в Калифорнийском университете в Беркли в 1999 году совпала с ее работой в Кремниевой долине во время бума доткомов; и переход от штатной должности в Беркли к штатной должности в Принстонском университете в 2003 году означал, что их маленькие дочери могли расти в более тихом городке, в то время как Инна Окункова переезжала в соседний Нью-Йорк.Когда его старшая дочь поступила в колледж в Принстоне, остальные члены семьи переехали в 2010 году в суету большого города, когда Окуньков начал свою нынешнюю должность в Колумбийском университете, где он сейчас профессор математики Самуэля Эйленберга.
В другом счастливом происшествии математик Рахул Пандхарипанде (который позже стал советником Маулика) имел офис по соседству с офисом Окунькова в Чикаго. Когда Пандхарипанде, алгебраический геометр, опубликовал задачу, относящуюся к определенному числовому ряду, называемому числами Гурвица, Окуньков обратился к нему.Он понял, что может решить эту проблему, используя теорию представлений. Окуньков особенно стремился изучить алгебраическую геометрию, изучение кривых, представленных как решения полиномиальных уравнений (например, парабола y = x 2 ), и применить свои знания в области теории представлений. Сегодня Окуньков и Пандхарипанде являются наиболее частыми соавторами друг друга, опубликовав вместе более дюжины статей за последние два десятилетия.
На самом деле Окуньков опубликовал так много работ по алгебраической геометрии, что можно легко предположить, что он защитил диссертацию в этой области, – говорит Маулик, ныне профессор математики Массачусетского технологического института.«Тот факт, что есть несколько предметов, о которых вы могли догадаться, на самом деле это было его прошлое, является отражением его безумной широты».
Выращивание различных ветвей
Несмотря на то, что в его успешной семье, состоящей из двух карьер и плодотворном сотрудничестве, учитывалась интуиция, Окуньков, вероятно, все же добился бы успеха, если бы все разыгралось по-другому. Или, как он выразился, «как человек, занимающийся математической физикой, я понимаю, что наш мир в некотором роде случайен.Глупо пытаться максимизировать вещи “.
Математическая физика, как следует из названия, представляет собой область чистой математики, которая занимается проблемами физики. Эти проблемы происходят из «реального» или физического мира, а не из теоретических областей абстрактных математических исследований.
Мина Аганагич, еще один сотрудник Окунькова, называет математическую физику «очень, очень счастливым взаимодействием двух полей». Аганагик – физик из Беркли, который занимается теорией струн, разделом теоретической физики, который заменяет частицы «струнами» и пытается объяснить отношения между квантовой физикой и обычной механикой.Она говорит, что «теория струн дает математике контекст, своего рода дорожную карту».
«Если у вас есть какая-то абстрактная проблема (а таких в математике много), очень часто у вас либо нет интуиции, либо у вас нет способа оценить важность и взаимосвязь этой проблемы», – объясняет Окуньков. . «Удивительно и замечательно, что математическая физика имеет всевозможные контексты».
Физика – не единственная область, затронутая работами Окунькова. Одна из классических проблем химии касается комбинаторики молекул, которая включает в себя подсчет количества способов, которыми молекулы могут склеиваться вместе.Окуньков признал, что он может применить алгебраическую геометрию к проблеме со своим соавтором Риком Кеньоном.
«Это было большим сюрпризом, поскольку люди, которые занимались классической алгебраической геометрией, привыкли работать с некоторыми большими измерениями и некоторыми загадочными областями», – говорит Кеньон, который работает в области комбинаторики и теории вероятностей. «Они действительно далеки от физики и от реального мира».
Опять же, склонность Окунькова прокладывать свой собственный путь привела к неожиданной связи в математическом генеалогическом древе.Фактически, методы, которые он и Кеньон разработали в своих решениях, привели к захватывающим результатам как в теории вероятностей, так и в алгебраической геометрии, добавив больше цветов в разрозненные области.
Статьи MNOP: развитие новой отрасли
Физик Никита Некрасов вспоминает, как познакомился с Окуньковым в Принстоне, где Некрасов учился в аспирантуре, когда Окуньков проводил весну 1996 года в Институте перспективных исследований. Спустя годы, в 2002 году, Некрасов «совершенно случайно» столкнулся с Окуньковым на железнодорожной платформе под Парижем, и между ними завязался разговор.Некрасов застрял на последнем этапе доказательства одной из своих гипотез, который, по его мнению, был связан с суммированием диаграмм Юнга – техникой, используемой в теории представлений.
«Его глаза стали туманными и мечтательными, и он сказал:« О, как интересно », – вспоминает Некрасов, ныне физик в Центре геометрии и физики Саймонса в Нью-Йорке. На следующее утро он написал мне электронное письмо: «Нам очень повезло, что мы встретились, потому что суммировать диаграммы Янга – это то, что я делаю от заката до рассвета и от рассвета до заката.Так что, возможно, я смогу помочь вам с вашим предположением ».
Эта помощь комбинаторики была ключом к завершению доказательства гипотезы Некрасова, которая связывает несколько разделов физики, как работа Окунькова связывает разделы математики. Доказательство, которое напрямую связано с работой Кеньона и Окунькова, основано на явлении, которое возникает в различных областях математики и физики: мы можем предсказать, как случайные процессы в малом масштабе могут закончиться в большом масштабе. Например, кристаллы растут, когда молекулы склеиваются в определенном формате.
«Это предположение было камнем, закрывающим вход в пещеру, полную сокровищ», – говорит Некрасов. «Как только мы выбили этот камень, мы обнаружили, что это только начало очень красивой истории».
Вдохновленные ростом кристаллов и работой Окунькова с несколькими другими математиками и физиками, Некрасов и Окуньков приступили к исследованию трехмерных диаграмм Юнга. Из этой работы они получили некоторые хорошо известные результаты, опубликованные совместно с Мауликом и Пандхарипанде в 2006 году.Эти основополагающие документы «MNOP» (названные в честь объединенных инициалов авторов) заложили основу для перечислительной геометрии, которая изучает количество кривых, удовлетворяющих различным геометрическим условиям.
Эти статьи представляют собой следующую главу в саге, которая началась в 1970-х и 1980-х годах отдельными публикациями математика Михаила Громова и физика Эдварда Виттена. В теории струн расположение каждой «струны» в пространстве-времени можно рассматривать как сложную кривую и, следовательно, анализировать с помощью инструментов алгебраической геометрии.В 1990-х годах исследователи объединили результаты Громова и Виттена, чтобы сформировать теоретическую основу для подсчета этих кривых в различных геометриях. В статьях MNOP было высказано предположение, что для определенного класса форм счет Громова-Виттена в точности соответствует тому, что они называют теорией Дональдсона-Томаса, которая использует совершенно иное понимание кривых. Эта теория основана на работе математиков Саймона Дональдсона и Ричарда Томаса по алгебраической геометрии 1998 года.
Эта удивительная связь, в соответствии с мотивом Окунькова соединять разрозненные области, проложила путь для целой области, ищущей сходные соответствия.Четыре соавтора выиграли престижную первую премию Compositio Prize в 2009 году за свою работу, описанную в заявлении о награде как «выдающееся математическое исследование».
Учим будущее
В дополнение к отмеченным наградами исследованиям, Окуньков также привносит свои уникальные взгляды в учебную и служебную части своей работы. Генри Лю, один из его нынешних аспирантов в Колумбийском университете, выбрал Окунькова в качестве советника после прохождения вводного курса аспирантуры по группам и представлениям Лжи.
«Сначала я был просто потрясен тем, насколько я смущен», – смеется Лю. «Обычно для групп Ли есть довольно канонический подход к этому с педагогической точки зрения. Андрей не придерживался такого подхода. В конце концов, я пришел к выводу, что его взгляд на все это очень красивый ».
Во время пандемии COVID-19 Окуньков организовал еженедельную летнюю школу Zoom по перечислительной геометрии и теории геометрических представлений. В итоге он продолжил серию из 33 лекций, которые продлились до 29 декабря, с видео и примечаниями к курсу, размещенными в Интернете.Этот подвиг свидетельствует о приверженности Окунькова образованию. Мелисса Лю, его коллега из Колумбийского университета, которая разделяет с ним грант на исследовательский кластер, говорит: «Он проделал огромную работу по обучению молодого поколения, не только своих собственных студентов и постдоков в Колумбии, но и молодых исследователей по всему миру. . »
Одним из самых гордых достижений Окунькова была совместная организация семестровой программы математической физики в 2018 году с Aganagic и другими в Исследовательском институте математических наук в Беркли.Он называет это «самым счастливым временем в моей профессиональной жизни», когда его окружали коллеги со всего мира, все сосредоточенные на задачах перечислительной геометрии.
В последнее время Окуньков продолжал участвовать в организации Международного конгресса математиков, который собирается раз в четыре года и будет проходить в Санкт-Петербурге в июле 2022 года. Его ежегодные поездки в Россию в течение лета привели к тому, что он руководил лабораторией, специализирующейся на математическая физика и теория представлений, совместно используемые двумя крупнейшими исследовательскими университетами России.
Почти все математики мира имеют записи в проекте по математической генеалогии, огромном онлайн-генеалогическом древе с изображением советников и советников за последние несколько столетий. Окуньков, у которого на дереве есть 10 потомков, теперь видит, как его собственные дети присоединяются к мировым ученым. Его младшая дочь готовится к поступлению в аспирантуру по физике, а его старшая дочь работает в Институте Флэтайрон Фонда Саймонса научным сотрудником по вычислительной астрофизике.Много лет назад Окуньков читал математические лекции в их средней школе, отражая его веру в аполитичную универсальность этой области.
«Есть еще много-много недостатков, но в принципе математику можно сделать абсолютно бесплатной и абсолютно универсальной», – говорит Окуньков. «Математика может быть абсолютно демократичной и очень доступной для всех. Это нужно всем ».
Профиль: Три общества ученых математиков | The Independent
Это знамение времен, когда общества ученых математиков, которые когда-то были заблокированы соперничеством, теперь делают все возможное, чтобы сотрудничать в интересах своего осажденного предмета.
Лондонское математическое общество (LMS) было основано еще в 1865 году, в период расцвета обществ ученых-ученых, примерно в то время, когда возникли Институт физики и Институт химии. LMS привлекала своих членов в основном из академических кругов и сосредоточила свои усилия на продвижении и публикации исследований в области чистой математики.
«Во многих отношениях мы были группой самопомощи, занимавшейся математикой, а не математиками», – говорит Питер Купер, исполнительный секретарь.«Мы сохранили свои корни: наша главная цель по-прежнему – продвигать эту тему, а не устанавливать стандарты или контролировать ее».
Но некоторые представители математического сообщества считали, что LMS не отражает их интересы, лежащие вне области чистой математики. Спустя почти 100 лет после основания LMS родился Институт математики и ее приложений (IMA) с более широким заданием, направленным на развитие математики в промышленности, бизнесе, государственном секторе, образовании и исследованиях.
В то время как LMS состоит из 2 500 членов, все из которых должны иметь докторскую степень по математике, IMA требует только степень математика и насчитывает более 5 300 членов (десять процентов из которых – иностранцы).В этом году IMA отмечает свое 40-летие, 30 процентов его членов – академические круги, 15 процентов – школы, 15 процентов – финансы, а остальные – промышленность и торговля.
«Мы стараемся быть всеобъемлющими, чтобы везде, где идет математика, у Института была своя роль», – объясняет Дэвид Юдан, исполнительный секретарь IMA.
Соперничество с LMS теперь в прошлом, говорит он. Настолько, что оба общества начали 18-месячный процесс обсуждения, чтобы «пересмотреть структуру» и даже рассмотреть возможность слияния.«IMA полностью поддержит слияние», – говорит Юдан.
Произойдет ли такое слияние, LMS и IMA уже участвуют в совместной инициативе по продвижению своего предмета вместе с третьим и старейшим математическим обществом, Королевским статистическим обществом (RSS). Эти трое сформировали Совет по математическим наукам в 1999 году. «Работая вместе, мы можем добиться гораздо большего эффекта в представлении правительству», – признает Питер Купер из LMS.
При финансовой поддержке Департамента образования и профессиональных навыков Совет разрабатывает ряд материалов по вопросам карьеры в виде брошюр и веб-сайтов для использования в школах.Все три общества разделяют широко распространенные опасения по поводу того, что математикой мало занимаются на уровне A-level и в университетах, и надеются, что они смогут внести свой вклад в стимулирование интереса молодых людей к этому предмету.
Варианты карьеры для математиков гораздо более разнообразны, чем многие думают, говорит Купер: «Часто задают вопрос, чем занимаются математики? Быстрый ответ: чем они не занимаются?»
Совет нацелен на учеников 10-го класса, чтобы убедить их продолжать заниматься математикой.Как утверждает Юдан: «Если вы свободно владеете математикой, неважно, какую работу вы выполняете, эти математические навыки будут жизненными навыками».
RSS сейчас усиленно работает над «расширением своей привлекательности», по словам генерального директора Айвора Годдарда. Основанный в 1834 году политиками и социологами, которые хотели сопоставить и свести в таблицу факты об обществе, RSS начал рассматривать методологическую сторону статистики в начале 20 века.
Эта тема получила большой импульс с появлением компьютеров в шестидесятые годы.Около трети из 6000 членов RSS вовлечены в государственную статистику, а многие другие – в промышленность (особенно фармацевтическую), а также в финансовые и актуарные процессы.
«Статистика – это очень современная дисциплина, несмотря на то, что мы очень старое общество», – говорит Годдард.
В Университете Ноттингем Трент RSS реализует проект переписи, в рамках которого дети собирают свои собственные данные и учатся их анализировать. RSS также опубликовал брошюру о том, как измерять риск, направленную на просвещение широкой общественности.
«Одна из наших трудностей заключается в том, чтобы избавиться от представления о том, что статистика скучна и имеет дело только с обработкой чисел», – говорит Годдард. «Мы хотим показать людям, что это живая тема».
Лондонское математическое общество: www.lms.ac.uk
Институт математики и ее приложений: www.ima.org.uk
Королевское статистическое общество: www.rss.org.uk
Дом
Maíra Aguiar | Центр прикладной математики Басков, Бильбао – Страна Басков, Испания
Марк Альбер (председатель) | Калифорнийский университет, Риверсайд, США
Пол Атцбергер | Калифорнийский университет, Санта-Барбара, США
Daniele Avitabile | Vrije Universiteit Amsterdam, Нидерланды
Эллен Бааке | Университет Билефельда, Германия
Марио Бануэлос | Калифорнийский государственный университет, Фресно, США
Mikahl Banwarth-Kuhn | Калифорнийский университет, Мерсед, США
J Олен Бриттон (ассистент кафедры) | Калифорнийский университет, Риверсайд, США
Санни Каник | Калифорнийский университет, Беркли, США
Уильям Кэннон | Тихоокеанская северо-западная национальная лаборатория, США
Вейтао Чен (заместитель председателя) | Калифорнийский университет, Риверсайд, США
Хейрим Чо | Калифорнийский университет, Риверсайд, США
Ят Тин Чоу | Калифорнийский университет, Риверсайд, США
Лизетт де Пиллис | Колледж Харви Мадда, США
Амина Эладдади | Колледж Сент-Роуз, Олбани, США
Немецкий Enciso | Калифорнийский университет, Ирвин, США
Марселла Гомес | Калифорнийский университет, Санта-Крус, США
Мелисса Гомес | Калифорнийский университет, Риверсайд, США
Jia Gou | Калифорнийский университет, Риверсайд, США
Роберт Гай | Калифорнийский университет в Дэвисе, США
Александр Хоффманн | Калифорнийский университет, Лос-Анджелес, США
Чиу-Йен Као | Колледж Клермонт Маккенна, США
Джэ Кён Ким | KAIST, Южная Корея
Pi Mu Epsilon Mathematics Honor Society – Школа теоретических и прикладных наук (TAS) |
О Пи Му Эпсилон:
Pi Mu Epsilon, Inc (PME), является Национальным математическим обществом чести.
Основанная 25 мая 1914 года в Сиракузском университете, PME в настоящее время имеет более 300 отделений в колледжах и университетах по всей территории Соединенных Штатов.
Целью Общества является содействие научной деятельности по математике среди студентов академических учреждений. – Сайт ПМЭ
О Пи Му Эпсилон – Нью-Джерси Глава:
Весной 2009 года в колледже Рамапо было учреждено отделение Nu в Нью-Джерси Пи Му Эпсилон. С тех пор каждый весенний семестр проводится вводная церемония, на которой новые члены вводятся в Национальное математическое общество Пи Му Эпсилон.
Любой студент колледжа Рамапо, который желает быть введенным в должность в Национальное математическое общество Пи Му Эпсилон через отделение Нью-Джерси Ню общества на данной церемонии весеннего семестра (например, на церемонии весны 2011 года), должен соответствовать следующим требованиям: конец предыдущего весеннего семестра (например, к концу весны 2010 г. соответственно):
- Студент закончил не менее двух курсов по математике.
- Студент закончил как минимум два курса математики, помимо математического анализа.
- У студента средний балл не ниже 3,0 по шкале 4,0.
- Студент имеет средний балл 3,0 по шкале 4,0 по курсам математики, пройденным на данный момент, которые приводят к выполнению требований для основной специальности по математике.
- Если у студента есть курсы, которые были переведены из других учебных заведений, по крайней мере два из четырех обязательных курсов, указанных в пунктах (1.) и (2.) выше, должны быть завершены в колледже Рамапо.
Как можно ввести в должность?
Каждый математик в колледже Рамапо каждый осенний семестр получает электронное письмо, в котором его или ее спрашивают, хотят ли они, чтобы их рассматривали для вступления в общество.Любой специалист по математике, который ответит на это электронное письмо к крайнему сроку, указанному в письме, будет рассматриваться для введения в должность и будет введен в должность, если он или она удовлетворяет 5 требованиям, перечисленным выше.
Любой студент колледжа Рамапо, не специализирующийся на математике (например, студент младшего математического или исторического), желающий быть введенным в должность, должен связаться с консультантом отделения, доктором Катаржиной Потоцкой, непосредственно по адресу kkowal @ ramapo .edu в начале осеннего семестра, который непосредственно предшествует весеннему семестру, в который студент хочет быть введен в должность.Любой такой не математический специальность будет введен в должность, если он или она удовлетворяет 5 требованиям, перечисленным выше.
Любой студент или частное лицо, не являющееся студентом колледжа Рамапо, или любой преподаватель, желающий быть введенным в общество исключительным действием, должен связаться с консультантом отделения напрямую по адресу [email protected] в начале осеннего семестра, предшествующего весеннему семестру, в котором они желают быть введены в должность.
Что вы будете делать после того, как попадете в Пи Му Эпсилон?
Цель Пи Му Эпсилон – способствовать научной деятельности в области математики.Поступившие в должность студенты колледжа Рамапо должны выполнять несколько увлекательных занятий в течение каждого учебного года. Такие мероприятия организует советник отделения. Также приглашенным студентам предлагается представить свои исследования по математике на местных, региональных и национальных конференциях. Вот несколько примеров таких конференций:
Дополнительная информация
Для получения дополнительной информации об обществе чести посетите национальный веб-сайт Пи Му Эпсилон (см. Отказ от ответственности ниже).
Колледж Рамапо в Нью-Джерси признает ценность публикации в Интернете. Колледж не выполняет предварительный просмотр, проверку, цензуру и не контролирует содержание этих страниц, как само собой разумеющееся. Эта страница и веб-страницы, на которые есть ссылки с этой страницы, созданы авторами и никоим образом не являются официальным содержанием Рамапо Колледжа Нью-Джерси.
Ингрид Добеши | Герцог Электротехника и компьютерная инженерия
Джеймс Б.Герцог, заслуженный профессор математики, электротехники и вычислительной техники
Назначения и членство
- Джеймс Б. Дюк, заслуженный профессор математики, электротехники и вычислительной техники
- Профессор кафедры математики
- Профессор кафедры электротехники и вычислительной техники
Контактная информация
- Адрес электронной почты: [email protected]
- Сайты:
Образование
- к.т.н. Брюссельский университет (Бельгия), 1980
Научные интересы
Теория вейвлетов, обработка сигналов, машинное обучение, вычислительная геометрия, частотно-временной анализ
Награды, почести и отличия
- Научная премия Фудань-Чжунчжи. Университет Фудань и группа предприятий Чжунчжи. 2018
- Избранный член.Национальная инженерная академия. 2015
- Цитируемый исследователь. Thomson Reuters. 2014
- Член Американской академии искусств и наук. Американская академия искусств и наук. 2013
- Премия Фонда BBVA Frontiers of Knowledge. BBVA Foundation Frontiers. 2013
- Премия за фундаментальные исследования. Немецкий фонд Эдуарда Райна. 2013
- Медаль Бенджамина Франклина в области электротехники. Институт Франклина. 2013
- Избранный член. Национальная академия наук.2013
- Эмили Нётер Лектор. Ассоциация женщин-математиков. 2013
- научный сотрудник. Американское математическое общество. 2013
- научный сотрудник. Институт инженеров по электротехнике и радиоэлектронике. 2013
- научный сотрудник. Фонд Макартура. 2013
- Премия «Золотой юбилей» за технологические инновации. Общество теории информации IEEE. 2013
- Сотрудник Гуггенхайма. Неизвестный. 2013
- Медаль Джека Килби за обработку сигналов. Институт инженеров по электротехнике и радиоэлектронике.2013
- Премия Лероя П. Стила за плодотворный вклад в исследования. Американское математическое общество. 2013
- Премия Луи Эмпена по физике. Неизвестный. 2013
- Премия Национальной академии наук по математике. Национальная академия наук. 2013
- Премия Неммерса по математике. Северо-Западный университет. 2013
- Пионерская премия. Международный совет по промышленной и прикладной математике. 2013
- Премия Рут Литтл Саттер по математике. Американское математическое общество.2013
- Премия Стила за математическую экспозицию. Американское математическое общество. 2013
- стипендиат AAAS. Американская ассоциация развития науки, The. 2011
- Медаль Бенджамина Франклина. Институт Франклина. 2011
- Медаль Джека С. Килби за обработку сигналов. Институт инженеров по электротехнике и электронике. 2011
- Лекция Джона фон Неймана. Общество промышленной и прикладной математики. 2011
- Премия Лероя П. Стила за плодотворный вклад в исследования.Американское математическое общество. 2011
- Стипендия. Мемориальный фонд Джона Саймона Гуггенхайма. 2010
- научный сотрудник. Общество промышленной и прикладной математики. 2009
- Членство. Американское философское общество. 2003
- Лекция Эрла Рэймонда Хедрика. Математическая ассоциация Америки. 2001
- Цитируемый исследователь. Thomson Reuters. 2001
- Премия NAS по математике. Национальная академия наук. 2000
- Премия Национальной академии наук по математике.Американское математическое общество. 2000
- научных сотрудников. Институт инженеров по электротехнике и электронике. 1999
- Школа математики / Члены. Институт перспективных исследований. 1999
- Члены / иностранные партнеры. Национальная академия наук. 1998
- Премия Рут Литтл Саттер по математике. Американское математическое общество. 1997
- Математическая выставка приза Лероя П. Стила. Американское математическое общество. 1994
- научных сотрудников. Американская академия искусств и наук.1993
- научных сотрудников. Фонд Макартура. 1992
- Школа математики / Члены. Институт перспективных исследований. 1990
Проведено курсов
- CHEM 89S: первый год семинара
- ECE 392: Проекты в области электротехники и вычислительной техники
- MATH 89S: первый год семинара
- MATH 112L: Лабораторный расчет II
- MATH 212D: многомерное исчисление
- MATH 240: Введение в прикладную математику: моделирование, уравнения и доказательства
- MATH 393: Независимое исследование
- MATH 635: Функциональный анализ
- MATH 712D: многомерное исчисление
В новостях
- Ингрид Добеши, Making Waves (28 января 2020 г.)
- Гарвард вручил Ингрид Добеши почетную степень (13 июня 2019 г.)
- Разговор с Ингрид Добешис: 8 советов по генерированию творческих идей (28 мая 2019 г. | Forbes)
- Добеши назван североамериканским лауреатом международной премии L’Oréal-ЮНЕСКО для женщин в науке (12 февраля 2019 г. | Pratt School of Engineering)
- Любимая теорема Ингрид Добешис: она использует графики, и биологи ее любят (6 августа 2018 г. | Scientific American)
- Математик Герцога наградил более 400000 долларов за вклад в теорию вейвлетов (30 июля 2018 г.)
- Герцог профессор получил приз в размере 100 000 долларов по прикладной математике (11 июня 2018 г.)
- Ингрид Добешис: Использование математики для ремонта шедевра (30 сентября 2016 г. | Quanta Magazine)
- Профессор математики Duke выигрывает 1 доллар.Премия в размере 5 миллионов (3 августа 2016 г. | The News & Observer)
- Фонд Саймонса вручил Ингрид Добешис грант Duke’s Ingrid Daubechies в размере 1,5 млн долларов (29 июля 2016 г.)
- Of Heartbeats, Bones and Brushstrokes (29 июля 2016 г.)
- Четыре факультета Пратта вошли в число наиболее цитируемых (26 января 2016 г.)
- Программное обеспечение помогает консерваторам искусства избавиться от колыбели (9 сентября 2015 г.)
- Ингрид Добешис о разрыве стеклянного потолка (17 июня 2015 г.)
- Визнер и Добеши названы членами Национальной инженерной академии (6 февраля 2015 г.)
- Добеши на первой женщине, получившей математическую медаль Филдса (14 августа 2014 г.)
- Комментарий Ингрид Добешис: Первый приз по математике получил первую победительницу женского пола (13 августа 2014 г. | The New York Times)
- Факультет Герцога направляется в Вашингтон, чтобы поговорить с политиками о математике и искусстве (16 июня 2014 г.)
Представительские публикации
- Форнасьер, М; Vybíral, J; Daubechies, I, Надежная и эффективная с точки зрения ресурсов идентификация мелких нейронных сетей по наименьшему количеству выборок , Информация и выводы, том 10, вып.2 (2021), стр. 625-695 [10.1093 / imaiai / iaaa036] [абс].
- Фулвуд, EL; Шан, S; Винчестер, JM; Кирвеслахти, Н; Ravier, R; Ковальский, С; Добеши, I; Boyer, DM, Понимание макроэволюционного моделирования и реконструкции предкового состояния радиационной и исторической диетической экологии Lemuriformes (приматы, млекопитающие). , BMC Ecology and Evolution, том 21, вып. 1 (2021) [10.1186 / s12862-021-01793-x] [абс].
- Daubechies, I; DeVore, R; Фукар, S; Ханин, Б; Петрова Г., Нелинейная аппроксимация и (глубокие) сети ReLU , Конструктивная аппроксимация (2021) [10.1007 / s00365-021-09548-z] [абс].
- Pu, W; Собер, B; Дэли, N; Хиггитт, К; Добеши, I; Родригес, MRD, Подход на основе подключенных автокодировщиков для разделения изображений с дополнительной информацией: с приложениями для исследования искусства , 2015 Ieee International Conference on Acoustics, Speech, and Signal Processing (Icassp), vol 2020 – May (2020), стр. 2213–2217 [10.1109 / ICASSP40776.2020.
51] [абс].
- Sabetsarvestani, Z; Собер, B; Хиггитт, К; Добеши, I; Родригес, MRD, Искусственный интеллект для исследований в области искусства: решение проблемы разделения рентгеновских изображений Гентского алтаря., Достижения науки, том 5, вып. 8 (2019) [10.1126 / sciadv.aaw7416] [абс].
Профиль школы – Школа естественных и математических наук Оклахомы
Университет штата Аризона – Темпе, Университет Бэйлора, Университет Белмонт, Бостонский колледж, Бостонский университет (4), Университет Брандейса, Калифорнийский технологический институт, Камеронский университет, Университет Кэмпбелла, Университет Карнеги-Меллона (3), Западный резервный университет Кейс Вестерн (3) , Колледж Атлантики, Колорадский колледж, Колорадская горная школа, Колумбийский университет (3), Университет Конкордия-Чикаго (3), Корнельский университет, Университет Дьюка Куншана, Университет Дьюка (3), Авиационный университет Эмбри-Риддла в Дейтона-Бич, Университет Эмори, Университет Эмори – Оксфордский колледж, Университет Джорджа Вашингтона, Гриннелл-колледж (2), Гамильтон-колледж, Гарвардский колледж (2), Колледж Харви Мадда, Университет Лихай, Массачусетский технологический институт (4), Южный государственный университет Миссури, Нью-Йорк Университет (2), Северо-Западный университет (4), Нова Юго-Восточный университет, Нью-Йоркский университет Шанхай, Оберлинский колледж, Университет Оклахома-Сити (2), Государственный университет Оклахомы (19), Государственный университет Орегона, Принсто n Университет (5), Университет Пердью (3), Политехнический институт Ренсселера, Университет Райса (4), Рочестерский технологический институт, Программа медицинских ученых Университета Сент-Луиса (2), Южный методистский университет, Юго-западный государственный университет Оклахомы (2), Стэнфорд Университет (3), Университет Алабамы, Техасский университет в Остине (7), Тринити-колледж в Дублине, Университет Тринити-Сан-Антонио (2), Университет Тулейна (2), Академия торгового флота США, Военно-морская академия США, Калифорнийский университет, Сан-Диего, Калифорнийский университет в Беркли, Калифорнийский университет в Лос-Анджелесе, Университет Центральной Оклахомы, Чикагский университет (5), Делавэрский университет, Канзасский университет, Мичиганский университет (2), Университет Миссури – Программа бакалавриата / доктора Канзас-Сити (2), Университет Северной Каролины в Чапел-Хилл, Университет Нотр-Дам (2), Университет Оклахомы (123), Университет Пенсильвании (5), Университет Портленда (2), Университет Рочестер, Университет o f Южная Калифорния (6), Университет Тампы, Университет Талсы (19), Университет Вандербильта (6), Колледж Вассара, Университет Вашингтона и Ли, Университет Вашингтона в Сент-Луисе (8), Уэслианский университет, Колледж Уильямса, Йельский университет
.