Модуль понятие – понятие, программный модуль, основные характеристики программного модуля, состав модулей программного продукта. — КиберПедия

Что такое модуль числа в математике

Термин (module) в буквальном переводе с латинского означает «мера». Это понятие было введено в математику английским учёным Р. Котесом. А немецкий математик К. Вейерштрасс ввёл в обращение знак модуля — символ, которым это понятие обозначается при написании.

Впервые данное понятие изучается в математике по программе 6 класса средней школы. Согласно одному из определений, модуль — это абсолютное значение действительного числа. Другими словами, чтобы узнать модуль действительного числа, необходимо отбросить его знак.

Графически абсолютное значение а обозначается как |a|.

Основная отличительная черта этого понятия заключается в том, что он всегда является неотрицательной величиной.

Числа, которые отличаются друг от друга только знаком, называются противоположными. Если значение положительное, то противоположное ему будет отрицательным, а ноль является противоположным самому себе.

Это интересно: умножение на 0 – правило для любого числа.

Геометрическое значение

Если рассматривать понятие модуля с позиций геометрии, то он будет обозначать расстояние, которое измеряется в единичных отрезках от начала координат до заданной точки. Это определение полностью раскрывает геометрический смысл изучаемого термина.

1. Для примера можно взять координатную прямую и на ней нанести 2 произвольные точки. Допустим, одна из точек (А) будет иметь числовое значение 5, а вторая (В) — 6.
2. Если рассмотреть полученный чертёж, можно увидеть, что точка, А находится на расстоянии 5 единиц от нуля (начала координат). Точка В находится от нуля на 6 единиц. Таким образом, модулем точки, А будет число 5, а модулем точки В — число 6.
3. В этом случае графическое обозначение выражения будет следующим: | 5 | = 5.
4. Иными словами, если взять любое произвольное число и обозначить его на координатной прямой в виде точки А, то расстояние от нуля до этой точки и будет модулем числа А.

Графически это можно выразить следующим образом: |a| = OA.

Это интересно: признак перпендикулярности прямой и плоскости, теория и практика.

Свойства абсолютной величины

Ниже будут рассмотрены все математические свойства этого понятия и способы записи в виде буквенных выражений:

1. Модулем любой цифры является величина неотрицательная. Таким образом, абсолютным значением положительной величины будет выступать она сама. Графически эта закономерность выражается следующим образом: |a| = a, если a> 0.
2. Модули противоположных величин равны друг другу Это объясняется тем фактом, что на координатной прямой противоположные числа хотя и располагаются в разных точках, но находятся на одинаковом расстоянии от начальной точки отсчёта. Графически это выражается как: |а| = |-а|.
3. Третьим свойством является то, что абсолютным значением нуля равняется сам нуль. Это условие считается верным в том случае, когда действительное число является нулем. Поскольку нулю соответствует начало отсчета в системе координат, то модулем числа ноль является сам ноль по определению. Графически: |0| = 0|.
4. Еще одним важным свойством является то, что абсолютное значение произведений двух любых действительных чисел равняется произведению двух этих величин. Это условие необходимо рассмотреть более подробно. Иначе говоря, абсолютным значением произведения величин, А и В будет АВ в случае если оба этих значения положительные или же оба отрицательные, или -АВ при условии, что одно из этих чисел будет отрицательным. В записи эта закономерность будет выглядеть следующим образом: |А*В| = |А| * |В|.
5. Абсолютная величина суммы любых двух действительных чисел меньше или равна сумме их модулей.
6. Абсолютная величина разности двух произвольных величин меньше или равна разности двух абсолютных величин.
7. Если в математическом выражении имеется постоянный положительный множитель, его можно выносить за знак | |.
8. Такое же правило распространяется и на показатель степени выражения.

Это интересно: что такое разность в математике?

Особенности решения уравнений с модулем

Если говорить о решении математических уравнений и неравенств, в которых содержится module, то необходимо помнить, что для их решения потребуется открыть этот знак.

К примеру, если знак абсолютной величины содержит в себе некоторое математическое выражение, то перед тем как раскрыть модуль, необходимо учитывать действующие математические определения.

|А + 5| = А + 5, если, А больше или равняется нулю.

5-А, если, А значение меньше нуля.

В некоторых случаях знак может раскрываться однозначно при любых значениях переменной.

Рассмотрим ещё одни пример. Построим координатную прямую, на которой отметим все числовые значения абсолютной величиной которых будет 5.

Для начала необходимо начертить координатную прямую, обозначить на ней начало координат и задать размер единичного отрезка. Кроме того, прямая должна иметь направление. Теперь на этой прямой необходимо нанести разметки, которые будут равны величине единичного отрезка.

Таким образом, мы можем увидеть, что на этой координатной прямой будут две интересующие нас точки со значениями 5 и -5.

obrazovanie.guru

модуль – это… Что такое модуль?

Модуль — (от лат. modulus  «маленькая мера»): В Викисловаре есть статья «модуль» Мо …   Википедия

МОДУЛЬ — (в математике) мера для сравнения однородных величин и для выражения одной из них помощью другой; м. выражается числом. Словарь иностранных слов, вошедших в состав русского языка. Павленков Ф., 1907. МОДУЛЬ (лат.). 1) число, которым множатся… …   Словарь иностранных слов русского языка

модуль — я, м. module <лат. modulus мера. 1. В строительном деле исходная единица измерения, устанавливаемая для данного сооружения или его частей. БАС 1. В архитектуре врач, зря быстрый свой успех, За модули ее принялся не на смех. Княжнин От дяди… …   Исторический словарь галлицизмов русского языка

МОДУЛЬ — (1) числовое значение какой либо характеристики, единица меры, коэффициент, число, показатель какого либо соотношения, напр.: а) М. зубчатого зацепления отношение шага зубчатого зацепления к числу π; умножив модуль на число зубьев шестерни,… …   Большая политехническая энциклопедия

МОДУЛЬ

— МОДУЛЬ, модуля, муж. (лат. modulus мерочка). 1. В точных науках название некоторых коэфициентов (физ.). Модуль упругости. Модуль сопротивления. || Число, на которое нужно умножить логарифм одной системы, чтобы получить логарифм другой системы… …   Толковый словарь Ушакова

МОДУЛЬ — (modulus) Величина числа с точки зрения его расстояния от 0. Модуль, или абсолютное значение реального числа х (обозначается |х|), является разностью между х и 0 независимо от знака. Следовательно, если х>0, то |х|=х и если х <0, то |х|=–х …   Экономический словарь

Модуль — (М) – характеристика универсальности, представляющая собой предпочтительное число размера формообразующих элементов, как правило, 100 мм. Длина формообразующих элементов выбирается кратно 3 м. [ГОСТ Р 52086 2003] Модуль [лат. modulus мера]… …   Энциклопедия терминов, определений и пояснений строительных материалов

МОДУЛЬ

— в радиоэлектронике, функционально законченный узел радиоэлектронной аппаратуры, оформленный конструктивно как самостоятельное изделие. Чаще всего модуль печатная плата с размещенными на ней интегральными схемами и другими деталями. Применяется в… …   Современная энциклопедия

МОДУЛЬ — комплексного числа см. Абсолютная величина. Модуль перехода от системы логарифмов при основании a к системе при основании b есть число 1/logab …   Большой Энциклопедический словарь

Модуль — в рекламе определенные размеры графической рекламы для публикации в прессе. См. также: Реклама в СМИ Периодические издания Финансовый словарь Финам …   Финансовый словарь

модуль — часть, устройство, узел Словарь русских синонимов. модуль сущ., кол во синонимов: 9 • веблет (1) • …   Словарь синонимов

dic.academic.ru

модуль – это… Что такое модуль?

02.01.13 модуль (линейная или многострочная символика штрихового кода) [module <linear or multi-row bar code symbology>] (1): Номинальная единица измерения линейного размера в знаке символа.

Примечание – В некоторых символиках ширина элемента может быть определена как кратное одного модуля. Модуль соответствует размеру X.

3.4 модуль: Часть ОИТ, которая выполняет определенную функцию и может содержать источники радиочастотных сигналов.

3.23 модуль: Устройство, например плата ввода-вывода, которая вставляется в соединительную плату или основной блок.

3.8 модуль (module): Элемент конструкции или сформированный набор подходящих друг к другу элементов конструкций в зданиях и сооружениях, или стандартная программа, дискретный компонент, или сформированный функциональный набор подходящих друг к другу стандартных программ или дискретных компонентов в электрической, электронной, программируемой электронной связанной с безопасностью зданий и сооружений системе.

2.8. Модуль – устройство, в корпусе которого совмещены функции хранения, получения и подачи огнетушащего вещества (ОТВ) при воздействии исполнительного импульса на пусковой элемент.

3.6 модуль : Строительная конструкция заводского изготовления со светопропускающим/несветопропускающим заполнением, монтируемая на строительном основании.

3.4 модуль: Часть оборудования информационных технологий, выполняющая определенную функцию и имеющая источники радиочастотных сигналов.

Модуль

Подсистема, которая включена в технологическую схему так, что сведения о ее состоянии в целом дают такую же информацию о состоянии системы, каткую и знание всех состояний подсистемы.

3.6 модуль: Унифицированная единица, входящая составной частью в совокупность сборочных единиц, оформленная конструктивно как самостоятельное изделие.

3.5 модуль: Устройство, в корпусе которого совмещены функции хранения и подачи ОТВ при воздействии пускового импульса на привод модуля.

3.3.6 модуль (module): Программа, дискретный компонент или функциональный набор инкапсулированных программ либо дискретных компонентов, объединенных между собой.

9 модуль: Функционально и конструктивно законченная составная часть аппаратуры, выполненная на базовых несущих конструкциях и характеризуемая необходимыми видами, межуровневой и внутриуровневой совместимости

2. Модуль

Условная линейная единица измерения, применяемая для координации размеров зданий и сооружений, их элементов, строительных конструкций, изделий и элементов оборудования

3.1.18 модуль (module): Малогабаритное устройство, не работающее самостоятельно, предназначенное для выполнения специализированных задач в сотрудничестве с хостом (например, модуль подсистемы условного доступа, модуль приложения электронного путеводителя по программам телевидения).

Смотри также родственные термины:

167 модуль (М)

Характеристика универсальности, представляющая собой предпочтительное число размера формообразующих элементов, как правило, 100 мм. Длина формообразующих элементов выбирается кратно 3 м

Определения термина из разных документов: модуль (М)

3.1 модуль (основной модуль): Исходная линейная условная единица измерения, применяемая для взаимосогласованности и координации размеров зданий и сооружений, их элементов, строительных конструкций, изделий и элементов оборудования. Основной модуль принят за основу для назначения других, производных от него модулей. Международное стандартизированное обозначение основного модуля «М».

3.3. модуль (сейфа, хранилища): Самостоятельная конструкция, позволяющая производить жесткое соединение с другими конструкциями сейфа или хранилища при его монтаже.

модуль (символа штрихового кода) : Номинальная единица длины в знаке символа линейной или многострочной символики штрихового кода, равная размеру X.

Примечание – В некоторых символиках ширина элементов может быть определена как кратное одного модуля

3.19 модуль (элемент): Отдельно собранный готовый рамный элемент с заполнением. Поле модуля может иметь светопрозрачное или непрозрачное заполнение; конструктивно и визуально разделено шпроссами, ригелями и стойками на более мелкие поля заполнения.

12 модуль вещательной программы: Телевизионная программа совместно с метаданными и данными пользователя телевизионной информации, подготовленная к выпуску.

24. Модуль взаимодействия факсимильного аппарата

Ндп. Индекс взаимодействия

Величина, определяемая отношением диаметра барабана к шагу развертки факсимильного аппарата.

Примечание. Модуль взаимодействия определяет возможность совместной работы факсимильных аппаратов с барабанной разверткой

24. Модуль внешних связей

Составная часть электрооборудования, предназначенная для подключения кабелей внешних связей до установки отдельных составных частей электрооборудования

14в. Модуль внешних связей системы управления техническими средствами корабля

Модуль внешних связей

Составная часть прибора системы управления техническими средствами корабля, являющаяся конструктивно законченным и индивидуально монтируемым на корабле изделием, предназначенным для ввода, закрепления, подключения, уплотнения внешних кабелей и механического объединения с приборной секцией

47. Модуль выключателя

Часть выключателя, имеющая законченное конструктивное оформление и рассчитанная на определенное напряжение или ток, которая при соединении с такими же частями создает возможность выполнения полюса выключателя на более высокие номинальные напряжения или токи

2.1. Модуль газового пожаротушения – баллон с запорно-пусковым устройством для хранения и выпуска газовых огнетушащих веществ.

3.1 модуль газового пожаротушения: Баллон с запорно-пусковым устройством для хранения и выпуска газовых огнетушащих веществ.

3.6 модуль георешетки : Единичный элемент георешетки минимальных размеров в растянутом состоянии.

3.1.11 модуль данных: Совокупность взаимосвязанных технических сведений по эксплуатации изделия, относящихся к определенной тематике и не допускающих дальнейшего их дробления на составные части.

модуль данных; МД (data module, DM): Совокупность взаимосвязанных технических сведений по эксплуатации изделия, относящихся к определенной тематике, не допускающая дальнейшего дробления на составные части

[ГОСТ 2.601, статья 3.1.11]

Модуль деформации – коэффициент пропорциональности линейной связи между приращениями давления на образец и его деформацией.

111 модуль деформации горной породы

Отношение приращения нормальных напряжений в горной породе к соответствующему приращению упругих и пластических деформаций

111 модуль деформации горной породы

Отношение приращения нормальных напряжений в горной породе к соответствующему приращению упругих и пластических деформаций

3.1.14 модуль деформации грунта: Обобщенная характеристика деформируемости грунта, представляющая собой коэффициент пропорциональности линейной связи между приращениями давления на образец и его деформацией.

3.10 модуль деформации и упругости : Деформационные характеристики слоя грунта, первая из которых зависит от величины нагрузки, а вторая – не зависит и является величиной постоянной.

71. Модуль дренажного стока

Количество воды, принимаемое осушительной сетью с единицы площади осушенных земель в единицу времени

3.4 модуль дренажного стока : Количество воды, принимаемое осушительной сетью с единицы площади осушенных земель в единицу времени.

[ГОСТ 26967-86, пункт 71]

23. Модуль ЕС СКТ

Функционально и конструктивно законченное устройство, состоящее из цифровых блоков и управляющих устройств с соответствующим программным обеспечением.

Примечание. В зависимости от назначения модуль ЕС СКТ принимает название: модуль цифрового коммутационного поля, модуль цифровых соединительных линий, модуль аналоговых соединительных линий, модуль служебных комплектов и др.

3.1.19 модуль защиты: Микропроцессорное устройство с центральным процессором, дескремблером, интерфейсами транспортного потока и команд, с шинной организацией.

3.3 модуль изотермический для жидкой двуокиси углерода: Теплоизолированный и термостатированный сосуд, оборудованный запорнопусковым устройством, холодильными агрегатами, приборами управления и контроля, предназначенный для хранения жидкой двуокиси углерода, а также для его подачи.

25. Модуль кислотности

Величина, определяемая отношением в процентах суммы окиси алюминия и двуокиси кремния к сумме окиси кальция и магния

17. Модуль коэффициента передачи тока биполярного транзистора на высокой частоте

D. Betrag der Kurzschlussstromverstärkung in Emitterschaltung bei HF

E. Modulus of the short-circuit forward current transfer ratio

F. Module du rapport de transfert direct du courant

|h_21э|

Модуль коэффициента передачи тока в схеме с общим эмиттером в режиме малого сигнала на высокой частоте

Модуль линейной деформации – показатель линейной деформируемости мерзлого грунта, отражающий отношение напряжений к вызванным относительным продольным деформациям.

13 модуль мультимедийной программы: Телевизионная программа, содержащая образовательные, телематические, интернет-совместимые, медиаметрические и телемедицинские данные, подготовленная к выпуску.

Модуль объектный

17

76

131 модуль орбитального средства: Конструктивно законченная составная часть орбитального средства, предназначенная для реализации целевых, управляющих и/или обеспечивающих функций самостоятельно или в составе орбитального средства.

3.4 модуль организации работ (модуль): системно упорядоченный набор типовых элементов организационно-технического механизма, характеризуемый определенной целевой направленностью, организационной законченностью и установленным для него порядком планирования, обеспечения и выполнения входящих в него элементов.

3.1.15 модуль осадки: Относительная деформация грунта, выраженная в промилях, определяемая по компрессионной кривой для заданной нагрузки.

2.3 модуль оценки (подтверждения) соответствия: Элементы процедуры оценки (подтверждения) соответствия, которые в определенном сочетании применяются для оценки (подтверждения) соответствия требованиям технического регламента.

3.13. Модуль пенного пожаротушения – устройство, совмещающее функции хранения и подачи пенообразователя или рабочего раствора пенообразователя в стационарную установку пожаротушения при воздействии пускового импульса на привод модуля.

121 модуль пластичности горной породы

Параметр, оценивающий пластичность горной породы и равный отношению прироста напряжений выше предела упругости к полной пластической деформации горной породы

121 модуль пластичности горной породы

Параметр, оценивающий пластичность горной породы и равный отношению прироста напряжений выше предела упругости к полной пластической деформации горной породы

Модуль пожаротушения – устройство, в корпусе которого совмещены функции хранения и подачи огнетушащего вещества при воздействии пускового импульса на привод модуля.

3.45 модуль пожаротушения : Устройство, в корпусе которого совмещены функции хранения и подачи огнетушащего вещества при воздействии пускового импульса на привод модуля.

3.48 модуль пожаротушения : Устройство, в корпусе которого совмещены функции хранения и подачи огнетушащего вещества при воздействии пускового импульса на привод модуля.

Модуль пожаротушения импульсный – модуль пожаротушения с продолжительностью подачи огнетушащего вещества до 1 с.

3.49 модуль пожаротушения импульсный : Модуль пожаротушения с продолжительностью подачи огнетушащего вещества до 1 с.

112 модуль полной деформации горной породы

Отношение предела прочности горной породы к ее предельной деформации

112 модуль полной деформации горной породы

Отношение предела прочности горной породы к ее предельной деформации

24. Модуль полной проводимости прямой передачи биполярного транзистора

D. Betrag des Übertragungsleitwerts vorwärts

E. Modulus of the short-circuit forward transfer admittance

F. Module de l’admittance de transfert direct

|y_21э|

Модуль полной проводимости прямой передачи в схеме с общим эмиттером

3.2 модуль порошкового пожаротушения; МПП: Устройство, в корпусе которого совмещены функции хранения и подачи огнетушащего порошка (ОП) при воздействии исполнительного импульса на пусковой элемент.

235. Модуль приведенного коэффициента преломления

Модуль преломления

4.4 модуль проверок: Набор связанных между собой проверок.

Модуль продольной упругости при расчетной температуре, МПа (кгс/см²)

E

Модуль продольной упругости материалов при расчетной температуре МПа (кгс/см²)

Е, Е₁, E₂, Е_к

Модуль продольной упругости при расчетной температуре, МПа (кгс/см²)

E

Модуль продольной упругости при расчетной температуре, МПа (кгс/см²)

E, E^t

63 модуль размеров тары: Наименьшая общая кратная величина, применяемая для координации и унификации размеров тары

31. Модуль размеров тары

D. Modul der Abmessungen für Verpackung

E. Module of container dimensions

F. Module des dimensions d’emballage

Наименьшая общая кратная величина, применяемая для координации и унификации размеров тары

Модуль сдвига – характеристика деформируемости, определяемая отношением интенсивности касательных напряжений к интенсивности деформаций сдвига.

Остальные термины, используемые в настоящем стандарте, приведены в ГОСТ 25100.

3.2 модуль сдвига (shear modulus) G: Отношение напряжения сдвига к соответствующей деформации ниже точки, где эта зависимость является линейной (см. рисунок 3).

3.2 модуль сдвига (shear modulus) G: Отношение напряжения сдвига к соответствующей деформации ниже точки, где эта зависимость является линейной (см. рисунок 3).

Модуль сдвига

G

Характеристика сопротивления материала изменению его формы при сохранении объема, численно равная отношению касательного напряжения, возникающего при чистом сдвиге, к соответствующей ему упругой деформации сдвига, кгс/см²

1. Модуль сдвига – отношение касательного напряжения к упругой угловой деформации в точке

3.2 модуль СИД (LED module): Элемент, представляющий собой источник света и состоящий из одного или нескольких светоизлучающих диодов, а также других компонентов, например оптических, механических, электрических и электронных, за исключением устройства управления.

Определения термина из разных документов: модуль СИД

3.3 модуль СИД со встроенным пускорегулирующим аппаратом (self-ballasted LED module): Модуль СИД, предназначенный для присоединения к источнику питания.

Примечание – Если модуль СИД со встроенным ПРА имеет ламповый цоколь, то его считают лампой со встроенным ПРА.

модуль символа матричной символики : Одиночная ячейка или элемент символа матричной символики, используемый для кодирования одного бита кодового слова

14. Модуль системы управления техническими средствами корабля

Модуль

Ндп. Субблок, кассета

Составная часть прибора или блока системы управления техническими средствами корабля, являющаяся конструктивно законченным легкосъемным, неремонтируемым в условиях корабля изделием, встраиваемым в прибор или блок системы управления.

Примечание. По конструктивному исполнению модуль может быть выполнен в соответствующей несущей или базовой несущей конструкции с установленными в ней платами (платой), электрорадиоизделиями или модулями низшего уровня

115 модуль спада горной породы

Коэффициент пропорциональности между напряжениями и продольными запредельными деформациями горной породы

115 модуль спада горной породы

Коэффициент пропорциональности между напряжениями и продольными запредельными деформациями горной породы

15. Модуль спектральной функции импульса

Ндп. Амплитудный спектр импульса

–

3.9 модуль управления : Программно-аппаратное устройство, преобразующее сигналы от системы первичной автоматики в управляющие воздействия на исполнительный механизм.

Примечание – В состав модулей управления входят также щиты, шкафы, посты.

3.10 модуль управления : Программно-аппаратное устройство, преобразующее сигналы от системы первичной автоматики в управляющие воздействия на исполнительный механизм (по title=”СТО НОСТРОЙ 2.15.8-2011 Инженерные сети зданий и сооружений внутренние. Устройство систем локального управления. Монтаж, испытания и наладка. Требования, правила и методы контроля”, пункт 3.9).

3.8 модуль упругости: Параметр, определяемый величиной деформации под воздействием нагружения, используется для характеристики прочности дорожных одежд.

Модуль упругости

Е

Характеристика сопротивления материала деформации при растяжении или сжатии, численно равная отношению напряжения, возникающего при растяжении или сжатии, к соответствующей ему упругой деформации, кгс/см²

18. Модуль упругости (начальный)

E_н

Отношение приращения напряжения к соответствующему приращению упругой деформации на начальном этапе нагружения

Модуль упругости бетона

Е_s

Коэффициент пропорциональности между нормальным напряжением и соответствующей ему относительной продольной упругомгновенной деформацией при s₁ = 0,3R_пр при осевом сжатии образца

Модуль упругости Е

Отношение приращения напряжения к соответствующему приращению удлинения в пределах упругой деформации

2. Модуль упругости нагретого до 200-300° бетона в зависимости от проектной марки бетона на сжатие приведен в табл. 2.

Таблица 2

Значения E_σt10^-4, Мн/м²

Бетон	Проектная марка бетона
	М100	M200	М300	М400	М500	М600	М700	М800
Тяжелый	1	1,4	1,7	2	2,2	2,3	2,3	2,4
На пористых заполнителях с плотностью, кг/м3:
1,4	0,6	0,7	0,8	–	–	–	–	–
1,8	0,7	0,9	1,1	1,2	–	–	–	–
2,2	–	1,1	1,3	1,4	–	–	–	–

Примечание. Для бетона тепловлажностной обработки при атмосферном давлении значения Е_σtумножаются на 0,9, а для бетона автоклавной обработки – на 0,77.

3.4 модуль упругости при сжатии (compression modulus of elasticity) E: Отношение напряжения сжатия к соответствующей относительной деформации образца при условии, что зависимость между этими характеристиками является прямо пропорциональной (см. рисунок 1).

3.4 модуль упругости при сжатии (compression modulus of elasticity) E: Отношение напряжения сжатия к соответствующей относительной деформации образца при условии, что зависимость между этими характеристиками является прямо пропорциональной (см. рисунок 1).

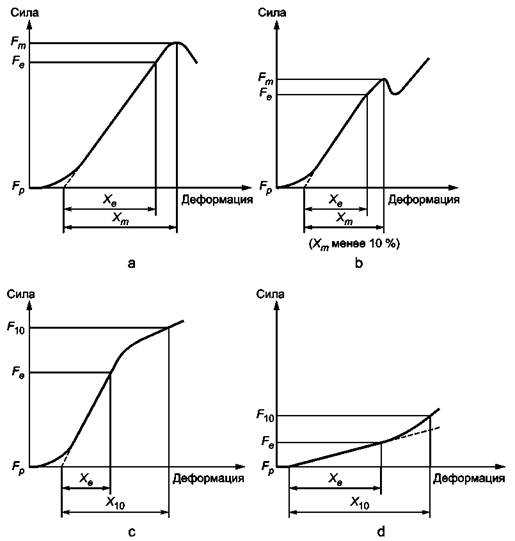
F_p – сила, соответствующая предварительной нагрузке; F_m – максимальная сила;

Рисунок 1 – Примеры графиков зависимости деформации образца от прилагаемой силы

3.4.53 модуль эластичности бумаги: Отношение усилия, необходимого для растяжения образца бумаги, отнесенного к площади поперечного сечения образца или к его удлинению.

Словарь-справочник терминов нормативно-технической документации. academic.ru. 2015.

normative_reference_dictionary.academic.ru

Понятие – модуль – Большая Энциклопедия Нефти и Газа, статья, страница 1

Понятие – модуль

Cтраница 1

Понятие модуля служит носителем фундаментального принципа, выработанного в алгебре почти сто лет назад.  [1]

Понятие модуля является естественным обобщением понятия векторного пространства: если взять в качестве А само поле / С, то / ( – модуль – это в точности векторное пространство.  [2]

Понятие модуля семейства кривых распространено на случай пространственных кривых и поверхностей.  [3]

Понятие модуля объемного сжатия ( сжимаемости) применимо не только к твердым телам, но и к жидкостям и газам. Сжимаемость газов зависит от того обратимого процесса, по которому производится сжатие.  [4]

Понятиями модуля расхода К и модуля скорости W широко пользуются при практических расчетах труб и каналов.  [5]

Установление понятий модуля красителя и модуля ванны представляет то преимущество, что в двух терминах дает точную научную количественную характеристику взаимных отношений трех основных участников крашения: волокна, красителя и ванны. Без модулей приходилось прибегать к сложным словесным формулировкам тех же взаимоотношений, используя различные единицы измерений и употребляя произвольные и не научные обозначения.  [6]

Обобщением понятия модуля кольцевой области является м о д у л ь пгу граничного э л е м е н-т а у открытой римановой поверхности R относительно его окрестности. В зависимости от того, конечна пли бесконечна величина т, граничный элемент имеет гиперболич. R обладает или нет Грина функцией.  [7]

С понятием модуля мы частично уже знакомы по предыдущей главе, где было рассмотрено понятие стандартной подпрограммы, так как последняя по сути дела является модулем.  [8]

Значит, понятие модуля действительного числа является частным случаем более общего понятия модуля комплексного числа.  [9]

Вебером введено понятие ведущего модуля группы классов.  [10]

Непосредственное применение понятия модуля позволяет доказать все элементарные теоремы об однолистных функциях. Действительно, Греч своим методом полос получил не только эти теоремы и их обобщения, но и некоторые замечательные новые результаты.  [11]

Таким образом, понятие модуля является дальнейшим развитием понятия подпрограммы, а последняя является частным случаем модуля, который программисты выделили и начали использовать раньше всего.  [12]

Норма является обобщением понятия модуля или длины вектора, известного из элементарной геометрии.  [13]

Следует сказать, что понятие модуля весьма неоднозначно, его даже можно считать неопределенным, однако правилу Рента это ничуть не мешает, пока подмодули в модуле соединяются друг с другом поверхностями.  [14]

Теперь ясно, что понятие модуля действительного числа – частный вид понятия модуля комплексного числа.  [15]

Страницы:      1    2    3    4

www.ngpedia.ru

Определение модуля | Математика

1. Определение модуля:

Модулем числа а называется расстояние (в единичных отрезках) от начала координат до точки А с координатой а.

Пример.

Модуль числа 7 равен 7, так как точка D с координатой 7 удалена от начала отсчета на 7 единичных отрезков.

Модуль числа -6 равен 6, так как точка С с координатой 6 удалена от начала отсчета на 6 единичных отрезков. Пишут:

   

2. По определению модуля, модуль — это расстояние.

А так как расстояние не может быть отрицательным числом, то и модуль не может быть отрицательным числом.

3. Модуль положительного числа равен самому числу.

Например,

   

4. Модуль отрицательного числа равен противоположному числу.

Например,

   

5. Модуль нуля равен нулю:

   

6. Противоположные числа имеют равные модули:

   

Например,

   

Из определения модуля:

www.for6cl.uznateshe.ru

1. Понятие модуля. Принципы модульного программирования. Понятие объекта как динамического модуля.

Модуль в программировании представляет собой функционально законченный фрагмент программы, оформленный в виде отдельного файла с исходным кодом, предназначенный для использования в других программах. Модули позволяют разбивать сложные задачи на более мелкие в соответствии с принципом модульности.

Модульное программирование – это организация программы как совокупности небольших независимых блоков, называемых модулями, структура и поведение которых подчиняются определенным правилам.

Использование модульного программирования позволяет упростить тестирование программы и обнаружение ошибок. Аппаратно-зависимые подзадачи могут быть строго отделены от других подзадач, что улучшает мобильность создаваемых программ.

Основные концепции модульного программирования:

-каждый модуль имеет единственную точку входа и выхода;

-размер модуля по возможности должен быть минимизирован;

-вся система построена из модулей;

-каждый модуль не зависит от того, как реализованы другие модули.

Классы очень удобно собирать в модули. При этом их описание помещается в секцию

interface, а код методов — в секцию implementation. Создавая модули классов, нужно

придерживаться следующих правил:

-все классы, предназначенные для использования за пределами модуля, следует

определять в секции interface;

– описание классов, предназначенных для употребления внутри модуля, следует

располагать в секции implementation;

– если модуль B использует модуль A, то в модуле B можно определять классы,

порожденные от классов модуля A.

2. Понятие класса. Понятие метода. Представление метода в виде обычной процедуры. Понятие конструктора и деструктора.

Каждый объект всегда принадлежит некоторому классу объектов. Класс объектов — это

обобщенное (абстрактное) описание множества однотипных объектов. Объекты являются

конкретными представителями своего класса, их принято называть экземплярами класса.

Например, класс СОБАКИ — понятие абстрактное, а экземпляр этого класса МОЙ ПЕС

БОБИК — понятие конкретное.

Для поддержки ООП в язык Delphi введены объектные типы данных, с помощью которых

одновременно описываются данные и операции над ними. Объектные типы данных

называют классами, а их экземпляры — объектами. Классы объектов определяются в секции type глобального блока. Описание класса начинается с ключевого слова class и заканчивается ключевым словом end. По форме объявления классы похожи на обычные записи, но помимо полей данных могут содержать объявления пользовательских процедур и функций. Процедуры и функции, предназначенные для выполнения над объектами действий, называются методами. Предварительное объявление методов выполняется при описании класса в секции interface модуля, а их программный код записывается в секции

implementation. Однако в отличие от обычных процедур и функций заголовки методов

должны иметь уточненные имена, т.е. содержать наименование класса.

Особой разновидностью методов являются конструкторы и деструкторы. Напомним, что

конструкторы создают, а деструкторы разрушают объекты. Создание объекта включает

выделение памяти под экземпляр и инициализацию его полей, а разрушение — очистку

полей и освобождение памяти. Действия по инициализации и очистке полей специфичны для каждого конкретного класса объектов. По этой причине язык Delphi позволяет

переопределить стандартный конструктор Create и стандартный деструктор Destroyдля

выполнения любых полезных действий. Можно даже определить несколько конструкторов и деструкторов (имена им назначает сам программист), чтобы обеспечить различные процедуры создания и разрушения объектов. Объявление конструкторов и деструкторов похоже на объявление обычных методов с той лишь разницей, что вместо зарезервированных слов function и procedure используются слова constructor и destructor.

studfiles.net

Модуль числа Википедия

График вещественной функции Модуль |z|{\displaystyle |z|} и другие характеристики комплексного числа z{\displaystyle z}

Абсолю́тная величина́, или мо́дуль числа x{\displaystyle x} (в математике) — неотрицательное число, определение которого зависит от типа числа x{\displaystyle x}. Обозначается: |x|{\displaystyle |x|}.

В случае вещественного x{\displaystyle x} абсолютная величина есть непрерывная кусочно-линейная функция, определённая следующим образом:

 |x|={  x,x⩾0−x, x<0{\displaystyle \ |x|={\begin{cases}\ \ x,&x\geqslant 0\\-x,&\ x<0\end{cases}}}

Обобщением этого понятия является модуль комплексного числа z=x+iy,{\displaystyle z=x+iy,} также иногда называемый абсолютной величиной^[1]. Он определяется по формуле:

|z|=|x+iy|=x2+y2{\displaystyle |z|=|x+iy|={\sqrt {x^{2}+y^{2}}}}

Основные свойства

С геометрической точки зрения, модуль вещественного или комплексного числа есть расстояние между числом и началом координат. В математике широко используется тот факт, что геометрически величина |x1−x2|{\displaystyle |x_{1}-x_{2}|} означает расстояние между точками x1{\displaystyle x_{1}} и x2{\displaystyle x_{2}} и, таким образом, может быть использована как мера близости одной (вещественной или комплексной) величины к другой.

Вещественные числа

• Область определения: (−∞;+∞){\displaystyle (-\infty ;+\infty )}.
• Область значений: [0;+∞){\displaystyle [0;+\infty )}.
• Функция чётная.
• Функция дифференцируема всюду, кроме нуля. В точке x=0{\displaystyle x=0} функция претерпевает излом.

Комплексные числа

Алгебраические свойства

Для любых вещественных чисел a,b{\displaystyle a,b} имеют место следующие соотношения:

•  |x|=x2=x⋅sgn⁡x=max{x,−x}{\displaystyle \ |x|={\sqrt {x^{2}}}=x\cdot \operatorname {sgn} x={\rm {max}}\,\{x,\,-x\}} (см. Функция sgn(x)).
• a⩽|a|{\displaystyle a\leqslant |a|}
• −|a|⩽a{\displaystyle -|a|\leqslant a}.
• Квадрат модуля числа равен квадрату этого числа: |a|2=a2{\displaystyle |a|^{2}=a^{2}}

Как для вещественных, так и для комплексных a,b{\displaystyle a,b} имеют место соотношения:

История

Считают, что термин предложил использовать Котс, ученик Ньютона. Лейбниц тоже использовал эту функцию, которую называл модулем и обозначал: mol x. Общепринятое обозначение абсолютной величины введено в 1841 году Вейерштрассом. Для комплексных чисел это понятие ввели Коши и Арган в начале XIX века.

В языках программирования

Поскольку эта функция вычисляется достаточно просто (только сравнениями и присваиванием), то обычно она входит в стандартный список функций во все языки программирования. Например, в Pascal есть функция abs(x), а в C fabs(x) для вещественного типа. В программе Wolfram Mathematica Abs[x].

Обобщение

Обобщением понятия модуля можно считать норму элемента многомерного векторного пространства, обозначаемую ‖x‖{\displaystyle \|x\|}. Норма вектора в евклидовом пространстве иногда тоже называется модулем. По аналогии с модулем разности чисел, норма разности двух векторов является мерой близости между ними. В отличие от модуля числа, норма вектора может определяться различными способами, однако в случае одномерного пространства норма вектора пропорциональна (часто и равна) модулю его единственной координаты.

См. также

Примечания

wikiredia.ru